【模型调优实战】：基于混淆矩阵的模型性能优化案例研究

# 1. 模型性能评估基础

在机器学习项目中，模型性能评估是一个至关重要的环节。它不仅仅是为了验证模型的准确性，更关乎于对模型预测结果的深入理解和质量控制。一个有效的评估体系能够帮助我们理解模型的优劣，并指导我们在后续的模型调优和迭代中做出合理的决策。本章节将介绍性能评估的基本概念和重要性，为接下来更深入的探讨混淆矩阵、模型调优方法论等内容打下基础。

# 2. 混淆矩阵的理论与应用

## 2.1 混淆矩阵的基本概念

### 2.1.1 真正类、假正类、真负类和假负类定义

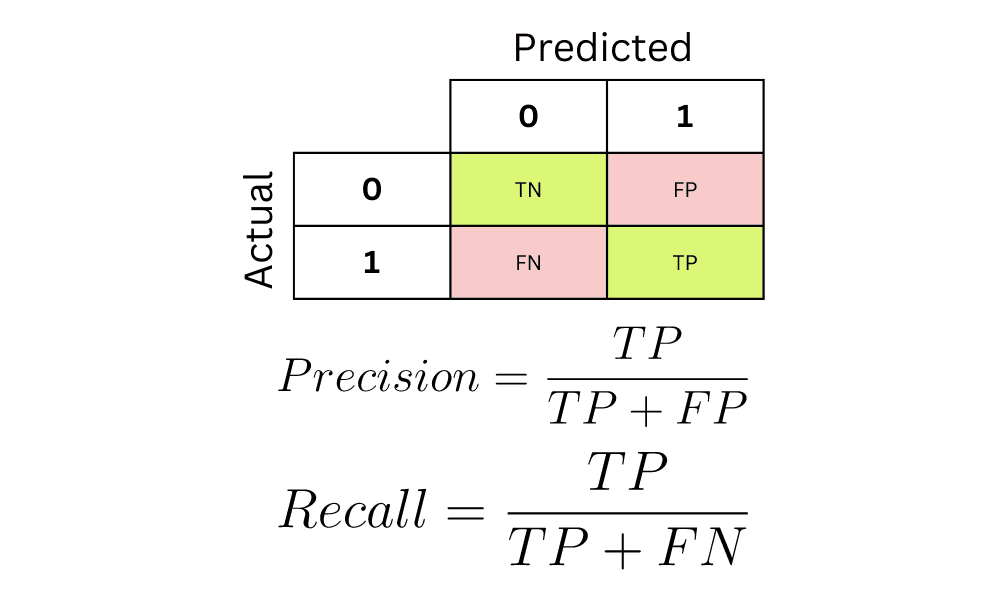
在分类问题中，混淆矩阵（Confusion Matrix）是评估模型性能的一个重要工具。混淆矩阵通过比较预测值与实际值，定义了四种基本结果：真正类（True Positive, TP）、假正类（False Positive, FP）、真负类（True Negative, TN）、假负类（False Negative, FN）。

- **真正类（TP）**：当模型正确预测出正类时，即实际标签为正，预测标签也为正的情况。
- **假正类（FP）**：模型错误预测出正类，实际上却是负类，即实际标签为负，预测标签为正。
- **真负类（TN）**：模型正确预测出负类，即实际标签为负，预测标签也为负。
- **假负类（FN）**：模型错误预测出负类，实际上应该是正类，即实际标签为正，预测标签为负。

这四个指标构成了混淆矩阵的四个基本单元，是进一步分析模型性能的基础。

### 2.1.2 混淆矩阵的结构和组成

混淆矩阵通常表示为一个二维数组的形式，其中行表示实际类别，列表示预测类别。对于二分类问题，一个典型的混淆矩阵如下所示：

              预测正类    预测负类
实际正类       TP          FN
实际负类       FP          TN

在多分类问题中，混淆矩阵将相应地扩展为多个类别，每一行和每一列代表一个不同的类别。混淆矩阵不仅能应用于二分类问题，还可以对多分类问题的每个类别分别进行分析。

## 2.2 混淆矩阵相关性能指标

### 2.2.1 精确率、召回率和F1分数

混淆矩阵的基础上，可以计算出一系列性能指标，以更全面地评估分类模型。最常用的指标包括精确率（Precision）、召回率（Recall）和F1分数。

- **精确率**定义为TP/(TP+FP)，即在所有预测为正类的样本中，实际为正类的比例。
- **召回率**定义为TP/(TP+FN)，即在所有实际为正类的样本中，被模型正确预测为正类的比例。
- **F1分数**是精确率和召回率的调和平均数，公式为2*(Precision*Recall)/(Precision+Recall)，它能平衡精确率和召回率，是模型性能的一种综合评价。

### 2.2.2 准确度、特异性和敏感性

除了上述指标，还有其他几个与混淆矩阵密切相关的性能指标：

- **准确度**（Accuracy）表示为(TP+TN)/(TP+FP+TN+FN)，即模型正确预测的比例。
- **特异性**（Specificity）反映的是在所有实际为负类的样本中，被模型正确预测为负类的比例，即TN/(TN+FP)。
- **敏感性**（Sensitivity）是召回率的另一种叫法。

通过对这些指标的理解，可以帮助我们深入分析模型在不同方面的性能，以及在不同应用场景下的适用性。

## 2.3 混淆矩阵在不同模型中的应用案例

### 2.3.1 二分类问题的混淆矩阵分析

在二分类问题中，混淆矩阵是最为直观和简单的评估模型性能的工具。例如，在医疗诊断领域，模型需要区分病人是否患有某种疾病。我们可以构建混淆矩阵来评价模型的预测结果：

from sklearn.metrics import confusion_matrix
import numpy as np

# 假设 y_true 是实际的标签，y_pred 是模型预测的标签
y_true = np.array([1, 0, 1, 1, 0, 0])
y_pred = np.array([1, 0, 1, 0, 0, 1])

# 计算混淆矩阵
conf_mat = confusion_matrix(y_true, y_pred)
print(conf_mat)

输出结果将是：

[[2 1]     # TN FN
 [1 2]]    # FP TP

通过分析这个混淆矩阵，我们可以计算出精确率、召回率等指标，从而对模型性能进行全面评估。

### 2.3.2 多分类问题的混淆矩阵分析

在多分类问题中，每个类别的混淆矩阵都可以独立分析，或者可以合并为一个总体混淆矩阵，以查看模型在所有类别上的表现。比如，在图像分类任务中，模型需要从多个类别中识别出对象，我们可以对每个类别分别构建混淆矩阵。

y_true = np.array([2, 0, 2, 2, 0, 1, 1, 2])
y_pred = np.array([2, 0, 1, 2, 0, 2, 1, 2])

conf_mat = confusion_matrix(y_true, y_pred)
print(conf_mat)

输出结果可能是：

[[2 0 1]     # TN FN FP
 [0 1 0]     # FP TN FP
 [1 1 1]]    # FP FN TP

模型的精确率、召回率等指标需要分别针对每一个类别进行计算，以便了解模型在各个类别上的预测能力。

在多分类问题中，每个类别的混淆矩阵都可以独立分析，或者可以合并为一个总体混淆矩阵，以查看模型在所有类别上的表现。比如，在图像分类任务中，模型需要从多个类别中识别出对象，我们可以对每个类别分别构建混淆矩阵。

y_true = np.array([2, 0, 2, 2, 0, 1, 1, 2])
y_pred = np.array([2, 0, 1, 2, 0, 2, 1, 2])

conf_mat = confusion_matrix(y_true, y_pred)
print(conf_mat)

输出结果可能是：

[[2 0 1]     # TN FN FP
 [0 1 0]     # FP TN FP
 [1 1 1]]    # FP FN TP

模型的精确率、召回率等指标需要分别针对每一个类别进行计算，以便了解模型在各个类别上的预测能力。

# 3. 模型调优的实战策略

## 3.1 参数优化的方法论

### 3.1.1 网格搜索和随机搜索

参数优化是机器学习模型调优中的关键环节，其目的是找到一组最优的模型参数以提升模型性能。在实际应用中，最常用的方法之一是网格搜索（Grid Search），另一种是随机搜索（Random Search）。

网格搜索通过遍历一个参数的指定范围内的所有可能组合来寻找最佳的参数组合。其优势在于方法简单，易于实现，并且可以通过全参数空间的穷举来确保找到全局最优解。然而，当参数量较大或参数范围较广时，网格搜索可能会变得异常耗时，因为其需要对每一个参数组合都进行模型训练和验证，导致计算成本极高。

随机搜索则是在预定义的参数空间中随机地选择参数组合，然后评估这些组合的性能。这种方法相较于网格搜索的优势在于能够在计算资源有限的情况下更快地收敛到好的参数组合。随机搜索之所以有效，是因为它能够在参数空间中快速探索到最有希望的区域，而不是逐一测试所有可能的组合。

以下是网格搜索和随机搜索的一个Python代码示例，假设我们使用`GridSearchCV`和`RandomizedSearchCV`来在`scikit-learn`库中进行调优：

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
from sklearn.svm import SVC
from scipy.stats import expon, reciprocal

# 加载数据集
iris = load_iris()
X, y = iris.data, iris.