混淆矩阵进阶教程：精通精确度、召回率与F1分数

# 1. 混淆矩阵基础与评估指标

在机器学习和数据挖掘的领域中，正确地评估一个分类模型的性能至关重要。混淆矩阵是一个非常基础且强大的工具，它为理解分类模型的性能提供了全面的视图。本章将为您介绍混淆矩阵的基础知识及其相关的评估指标，包括精确度、召回率和F1分数，并为后续章节中这些概念的应用和优化打下坚实的基础。

## 混淆矩阵的构成与分类评估指标

### 真正类、假正类、真负类和假负类

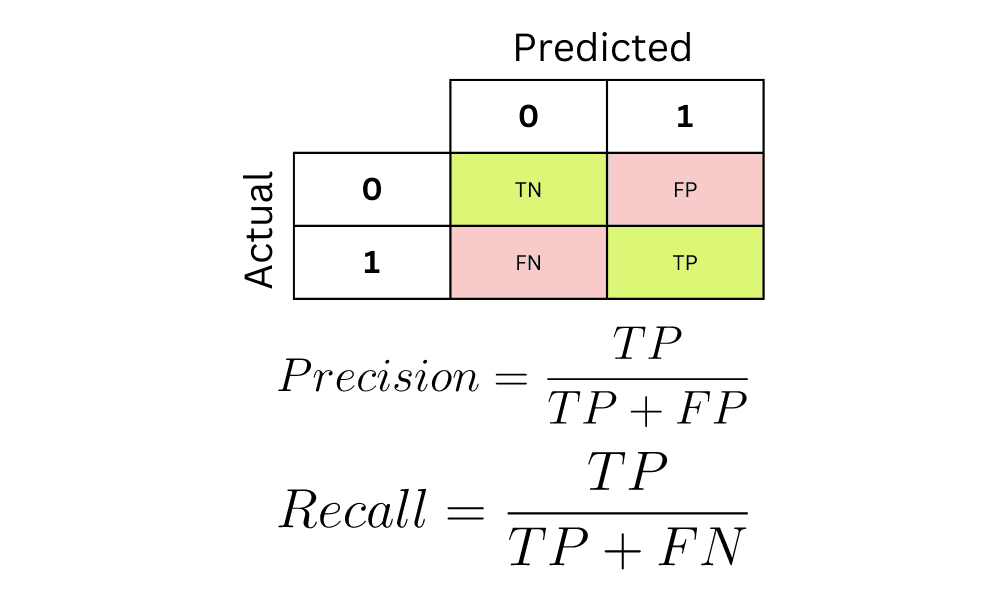
混淆矩阵是一个表格，它展现了模型分类结果与真实情况之间的关系。在二分类问题中，混淆矩阵由四个主要部分构成：
- 真正类（True Positives, TP）：模型正确预测为正类的数量。
- 假正类（False Positives, FP）：模型错误预测为正类的数量。
- 真负类（True Negatives, TN）：模型正确预测为负类的数量。
- 假负类（False Negatives, FN）：模型错误预测为负类的数量。

### 精确度和召回率的定义

精确度（Precision）和召回率（Recall）是基于混淆矩阵计算出的两个关键指标。
- 精确度表示模型预测为正类中实际为正类的比例。其计算公式为：精确度 = TP / (TP + FP)。
- 召回率表示模型检测出的正类占实际所有正类的比例。其计算公式为：召回率 = TP / (TP + FN)。

通过这些指标，我们能够从不同的角度评估模型的预测性能。下一章，我们将深入探讨精确度与召回率之间的关系以及F1分数的意义。

# 2. 精确度、召回率与F1分数的理论解读

## 2.1 混淆矩阵的构成与分类评估指标

### 2.1.1 真正类、假正类、真负类和假负类
混淆矩阵是评估分类模型性能的核心工具，它提供了四个基本的分类指标：真正类（True Positive, TP）、假正类（False Positive, FP）、真负类（True Negative, TN）和假负类（False Negative, FN）。这四个指标是理解和计算精确度、召回率和F1分数的基础。

- **真正类（TP）**：被模型正确预测为正类的样本数量。
- **假正类（FP）**：被模型错误预测为正类的样本数量。
- **真负类（TN）**：被模型正确预测为负类的样本数量。
- **假负类（FN）**：被模型错误预测为负类的样本数量。

对于一个二分类问题，混淆矩阵可以表示如下：

              预测为正类    预测为负类
实际为正类       TP              FN
实际为负类       FP              TN

### 2.1.2 精确度和召回率的定义
精确度（Precision）和召回率（Recall）是评估分类模型性能的两个常用指标，它们分别关注模型预测的正类中实际为正类的样本比例和模型覆盖到的实际正类样本的比例。

- **精确度（Precision）**：表示模型预测为正类的样本中实际为正类的比例。公式表示为：`Precision = TP / (TP + FP)`。精确度高表示模型对正类的预测较为准确。

- **召回率（Recall）**：表示实际为正类的样本中被模型正确识别为正类的比例。公式表示为：`Recall = TP / (TP + FN)`。召回率高表示模型能够更多地识别出实际为正类的样本。

## 2.2 精确度与召回率的关系

### 2.2.1 精确度和召回率的权衡
精确度和召回率之间的权衡是评估模型性能时的一个重要考量。在某些情况下，提高精确度可能会导致召回率降低，反之亦然。这种现象通常被称为“精确度-召回率权衡”（Precision-Recall Tradeoff）。

例如，在垃圾邮件检测中，如果一个模型被设计为非常保守，只有在非常确定一封邮件是垃圾邮件时才会将其标记出来，那么它的精确度可能会很高（因为标记为垃圾邮件的邮件大部分确实是垃圾邮件），但召回率可能会很低（因为很多垃圾邮件没有被识别出来）。相反，如果模型被设计为尽可能多地标记垃圾邮件，即使有些邮件实际上不是垃圾邮件，那么召回率会很高，但精确度会很低。

### 2.2.2 精确度和召回率的直观解释
为了更直观地理解精确度和召回率之间的关系，可以考虑以下表格，它展示了在不同阈值下模型对正类样本的预测情况：

| 阈值 | TP | FP | TN | FN | 精确度 | 召回率 |
|------|----|----|----|----|--------|--------|
| 0.9 | 80 | 20 | 70 | 30 | 0.8 | 0.73 |
| 0.7 | 90 | 50 | 50 | 20 | 0.64 | 0.82 |
| 0.5 | 100| 100| 0 | 10 | 0.5 | 0.91 |

在这个例子中，当阈值为0.9时，模型较为保守，精确度较高，但召回率较低。而当阈值降到0.5时，模型更加积极预测正类，召回率提高，但精确度降低。因此，选择合适的阈值来平衡精确度和召回率取决于具体的应用场景和需求。

## 2.3 F1分数的意义与计算方法

### 2.3.1 F1分数的定义和公式
F1分数是精确度和召回率的调和平均数，它试图在两者之间找到一个平衡点。F1分数的计算公式为：

F1 = 2 * (Precision * Recall) / (Precision + Recall)

F1分数的取值范围是[0, 1]，F1分数越高表示模型的综合性能越好。F1分数对精确度和召回率同等重视，因此它是一个有效的衡量指标，尤其是当精确度和召回率都很重要时。

### 2.3.2 F1分数与精确度和召回率的关系
F1分数综合考虑了精确度和召回率，避免了单独使用任一指标可能带来的片面性。在实际应用中，模型在特定场景下的性能可能会因为类别不平衡而受到质疑。例如，如果在一个数据集中正类样本的数量远多于负类样本，那么即使模型只是简单地预测所有样本为正类，也可能获得很高的准确率。然而，这样的模型几乎没有实际应用价值。

F1分数的使用可以减少这种类不平衡带来的影响。通过均衡考虑精确度和召回率，F1分数可以更准确地评估模型在处理不平衡数据集时的真实性能。因此，F1分数在处理不平衡数据集时是一个非常有用的评估指标。

在下一章节中，我们将通过实例进一步分析混淆矩阵的实践应用，并讨论精确度、召回率和F1分数在具体问题中的计算和应用。

# 3. 混淆矩阵的实践分析

在前两章中，我们已经对混淆矩阵的基础知识以及精确度、召回率和F1分数进行了理论上的讨论。现在，我们将深入实践，通过实例来分析这些评估指标在分类问题中的应用，并探讨在实际操作中可能遇到的问题和解决方案。

## 3.1 分类问题的混淆矩阵应用实例

### 3.1.1 二分类问题的混淆矩阵应用

在二分类问题中，混淆矩阵被用来总结模型的预测结果。它将数据分为四个部分：真正类（TP），假正类（FP），真负类（TN）和假负类（FN）。下面我们通过一个简单的例子来理解二分类问题的混淆矩阵。

假设有一个垃圾邮件过滤器，需要将邮件分为"垃圾"（Spam）和"非垃圾"（Not Spam）。我们有以下的数据：

实际\预测  预测为Spam