MATLAB频谱分析：信号处理的秘密武器，18个实战案例从入门到精通

# 1. 频谱分析基础**

**1.1 频谱分析的概念和重要性**

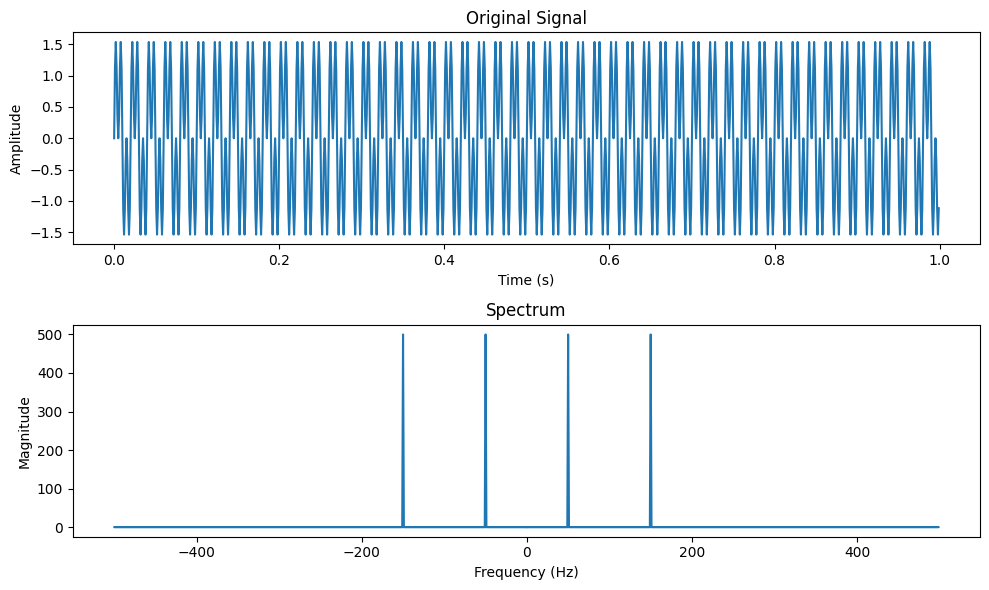
频谱分析是一种将信号分解为其组成频率分量的技术。它可以揭示信号中隐藏的信息，例如信号的频率组成、能量分布和相位关系。频谱分析在信号处理、通信和医学等领域有着广泛的应用。

**1.2 傅里叶变换在频谱分析中的作用**

傅里叶变换是频谱分析的关键工具。它将时域信号转换为频域信号，其中信号的频率分量被分离出来。傅里叶变换揭示了信号的频率内容，使我们能够分析和理解信号的特性。

# 2. MATLAB频谱分析工具箱

MATLAB频谱分析工具箱是一个功能强大的工具集，用于执行各种频谱分析任务。它提供了一系列函数，可以生成频谱图、功率谱密度图和相位图。

### 频谱分析工具箱概述

MATLAB频谱分析工具箱包含用于频谱分析的各种函数。这些函数可以分为以下几个类别：

- **频谱图生成函数：**这些函数用于生成频谱图，显示信号的幅度或功率随频率的变化。
- **功率谱密度图生成函数：**这些函数用于生成功率谱密度图，显示信号的功率随频率的变化。
- **相位图生成函数：**这些函数用于生成相位图，显示信号的相位随频率的变化。

### 频谱图、功率谱密度图和相位图的生成

**频谱图生成**

频谱图显示信号的幅度或功率随频率的变化。可以使用`fft`函数计算信号的傅里叶变换，然后使用`plot`函数绘制频谱图。

% 生成正弦波信号
t = 0:0.01:1;
x = sin(2*pi*10*t);

% 计算傅里叶变换
X = fft(x);

% 绘制频谱图
plot(abs(X));
xlabel('Frequency (Hz)');
ylabel('Amplitude');
title('Spectrum of a Sine Wave');

**功率谱密度图生成**

功率谱密度图显示信号的功率随频率的变化。可以使用`pwelch`函数计算信号的功率谱密度，然后使用`plot`函数绘制功率谱密度图。

% 生成正弦波信号
t = 0:0.01:1;
x = sin(2*pi*10*t);

% 计算功率谱密度
[Pxx, F] = pwelch(x, [], [], [], 100);

% 绘制功率谱密度图
plot(F, 10*log10(Pxx));
xlabel('Frequency (Hz)');
ylabel('Power Spectral Density (dB)');
title('Power Spectral Density of a Sine Wave');

**相位图生成**

相位图显示信号的相位随频率的变化。可以使用`angle`函数计算信号的相位，然后使用`plot`函数绘制相位图。

% 生成正弦波信号
t = 0:0.01:1;
x = sin(2*pi*10*t);

% 计算相位
phase = angle(x);

% 绘制相位图
plot(phase);
xlabel('Frequency (Hz)');
ylabel('Phase (radians)');
title('Phase of a Sine Wave');

### 频谱分析工具箱的常见函数

MATLAB频谱分析工具箱包含用于频谱分析的各种常见函数。这些函数包括：

- `fft`：计算信号的傅里叶变换。
- `ifft`：计算信号的逆傅里叶变换。
- `pwelch`：计算信号的功率谱密度。
- `spectrogram`：计算信号的时频谱图。
- `sphase`：计算信号的相位。
- `unwrap`：解开信号的相位。

# 3. 频谱分析实战案例

**3.1 信号噪声比（SNR）的计算**

信号噪声比