MATLAB频谱分析：信号处理中的高级技术，16个实战案例揭秘

# 1. MATLAB频谱分析基础**

MATLAB频谱分析是利用MATLAB软件对信号进行频域分析的一种技术，它可以将时域信号转换为频域信号，从而揭示信号中隐藏的频率信息。频谱分析在信号处理、语音处理、图像处理等领域有着广泛的应用。

MATLAB中提供了丰富的频谱分析函数，如`fft`、`ifft`、`spectrogram`等。这些函数可以帮助用户快速、高效地进行频谱分析。通过对频谱的分析，可以提取信号的频率、幅度、相位等特征，从而为信号的处理和理解提供重要的依据。

# 2. MATLAB频谱分析技术

### 2.1 时域与频域分析

#### 2.1.1 时域信号与频域信号

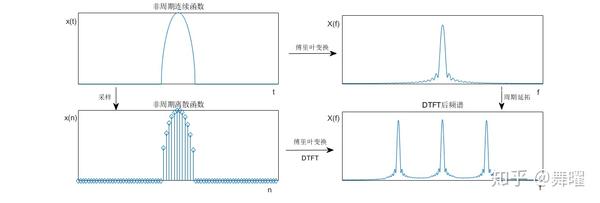
时域信号是指在时间域上变化的信号，它描述了信号随时间变化的幅度和相位。频域信号则是时域信号的傅里叶变换，它描述了信号在频率域上的幅度和相位分布。

**时域信号特点：**

* 直观，易于理解
* 反映信号的瞬时变化
* 适用于非平稳信号

**频域信号特点：**

* 揭示信号的频率成分
* 适用于平稳信号
* 便于信号处理和分析

#### 2.1.2 傅里叶变换与逆傅里叶变换

傅里叶变换是将时域信号转换为频域信号的数学运算，逆傅里叶变换则是将频域信号转换为时域信号的运算。

**傅里叶变换公式：**

X(f) = ∫_{-\infty}^{\infty} x(t) e^(-j2πft) dt

**逆傅里叶变换公式：**

x(t) = ∫_{-\infty}^{\infty} X(f) e^(j2πft) df

**傅里叶变换性质：**

* 线性
* 时移不变性
* 频率缩放不变性
* 卷积定理

### 2.2 频谱估计方法

频谱估计是根据有限长度的时域信号估计其频谱的方法。常用的频谱估计方法包括：

#### 2.2.1 周期图法

周期图法是将时域信号分成多个周期，然后计算每个周期的频谱。其优点是计算简单，但仅适用于周期信号。

**周期图法步骤：**

1. 将时域信号分成多个周期
2. 对每个周期进行傅里叶变换
3. 取平均得到频谱

#### 2.2.2 非参数方法

非参数方法不假设信号的统计特性，直接从时域信号估计频谱。常用的非参数方法有：

* **Welch法：**将时域信号分成多个重叠的片段，对每个片段进行傅里叶变换，然后取平均得到频谱。
* **Bartlett法：**与Welch法类似，但片段不重叠。
* **汉宁窗法：**在Welch法或Bartlett法的基础上，对片段应用汉宁窗以减少频谱泄漏。

#### 2.2.3 参数方法

参数方法假设信号服从某种统计分布，然后根据参数估计频谱。常用的参数方法有：

* **自回归（AR）模型：**假设信号服从自回归模型，通过估计模型参数得到频谱。
* **自回归滑动平均（ARMA）模型：**假设信号服从ARMA模型，通过估计模型参数得到频谱。
* **自回归移动平均（ARIMA）模型：**假设信号服从ARIMA模型，通过估计模型参数得到频谱。

# 3.1 信号预处理

在进行频谱分析之前，通常需要对原始信号进行预处理，以提高频谱分析的准确性和可靠性。信号预处理的主要目的是去除信号中的噪声和干扰，并平滑信号，使频谱分析结果更加清晰。

#### 3.1.1 数据去噪

数据去噪是信号预处理中的重要步骤，其目的是去除信号中不必要的噪声和干扰，提高信噪比。常用的数据去噪方法包括：

- **均值滤波：**对信号的每个数据点，用其邻近点的平均值替换，从而平滑信号并去除噪声。
- **中值滤波：**对信号的每个数据点，用其邻近点的中值替换，可以有效去除椒盐噪声和脉冲噪声。
- **小波变换：**利用小波变换将信号分解成不同尺度的子带，然后对每个子带进行去噪处理，最后重构信号。

% 均值滤波
data_denoised = filter(ones(1, 5) / 5, 1, data);

% 中值滤波
data_denoised = medfilt1(data, 5);

% 小波变换去噪
[cA, cD] = dwt(data, 'db4');
cD_denoised = wden(cD, 'rigrsure', 's', 'mln', 5);
data_denoised = idwt(cA, cD_denoised, 'db4');

#### 3.1.2 数据平滑