MATLAB遗传算法实战：一步步掌握原理、步骤和应用

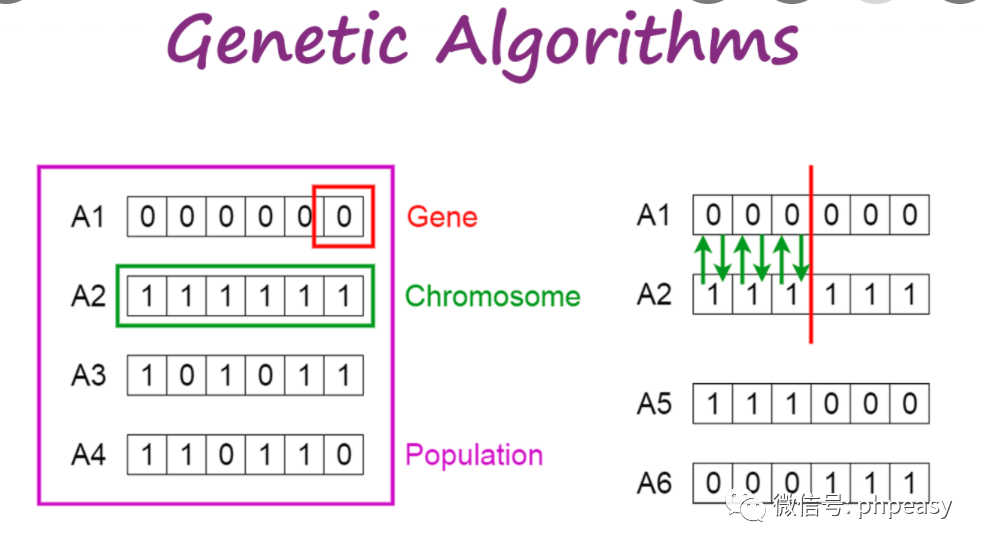
# 1. 遗传算法基础理论**

遗传算法是一种受生物进化过程启发的优化算法。它通过模拟自然选择、交叉和突变等进化机制，在搜索空间中寻找最优解。遗传算法的基本原理包括：

- **种群：**一组候选解，称为染色体。
- **适应度：**衡量每个染色体质量的函数。
- **选择：**基于适应度选择染色体进行繁殖。
- **交叉：**将两个染色体的一部分交换，产生新的染色体。
- **突变：**随机改变染色体的一部分，引入多样性。

# 2.1 遗传算法的MATLAB实现

### 2.1.1 基本框架

遗传算法在MATLAB中的基本框架如下：

% 初始化种群
population = initialize_population(population_size);

% 迭代进化
for generation = 1:max_generations
    % 评估种群
    fitness = evaluate_population(population);
    % 选择
    parents = select_parents(population, fitness);
    % 交叉
    children = crossover(parents);
    % 变异
    children = mutate(children);
    % 更新种群
    population = [population; children];
end

% 返回最优解
best_solution = find_best_solution(population);

### 2.1.2 关键函数

**初始化种群**：随机生成满足特定约束的个体集合。

**评估种群**：计算每个个体的适应度值，反映其解决问题的优劣程度。

**选择**：根据适应度值从种群中选择个体进行繁殖。

**交叉**：将两个父代个体的遗传信息结合起来产生新的个体。

**变异**：随机改变个体的遗传信息，引入多样性。

**更新种群**：将新产生的个体添加到种群中，并根据适应度值淘汰较差的个体。

**寻找最优解**：在种群中找到具有最高适应度值的个体。

### 2.1.3 参数优化

遗传算法的性能受多种参数影响，包括种群规模、选择压力、交叉概率和变异概率。优化这些参数至关重要，以获得最佳结果。

#### 2.1.3.1 种群规模

种群规模越大，算法搜索空间越大，找到最优解的可能性就越大。然而，较大的种群规模也需要更多的计算资源。

#### 2.1.3.2 选择压力

选择压力决定了适应度值较高的个体在选择过程中被选中的可能性。较高的选择压力会导致算法收敛速度更快，但也有可能陷入局部最优。

#### 2.1.3.3 交叉概率

交叉概率控制着父母个体遗传信息交换的频率。较高的交叉概率促进多样性，但也有可能破坏有用的遗传信息。

#### 2.1.3.4 变异概率

变异概率控制着个体遗传信息随机改变的频率。较高的变异概率引入多样性，但也有可能破坏有用的遗传信息。

### 2.1.4 代码示例

以下代码示例演示了如何使用MATLAB实现遗传算法：

% 问题定义
problem = struct('fitness_function', @my_fitness_function, 'num_variables', 10);

% 遗传算法参数
params = struct('population_size', 100, 'max_generations', 100, 'selection_pressure', 1.5, 'crossover_probability', 0.8, 'mutation_probability', 0.1);

% 初始化种群
population = initialize_population(problem, params.population_size);

% 迭代进化
for generation = 1:params.max_generations
    % 评估种群
    fitness = evaluate_population(problem, population);
    % 选择
    parents = select_parents(population, fitness, params.selection_pressure);
    % 交叉
    children = crossover(population, parents, params.crossover_probability);
    % 变异
    children = mutate(children, params.mutation_probability);
    % 更新种群
    population = [population; children];
end

% 返回最优解
best_solution = find_best_solution(population);

在这个示例中，`my_fitness_function`是自定义的适应度函数，`problem`结构体定义了问题，`params`结构体包含遗传算法参数。

# 3.1 优化函数

遗传算法在优化函数方面有着广泛的应用，因为它能够有效地搜索复杂函数的解空间，并找到全局最优解。在MATLAB中，可以使用 `ga` 函数进行函数优化。

**代码块：**

% 定义目标函数
fun = @(x) x^2 + sin(x);

% 设置遗传算法参数
options = gaoptimset('PopulationSize', 100, 'Generations', 100, 'Display', 'iter');

% 进行遗传算法优化
[x, fval, exitflag, output] = ga(fun, 1, [], [], [], [], -10, 10, [], options);

% 输出结果
fprintf('最优解：%f\n', x);
fprintf('最优值：%f\n', fval);

**逻辑分析：**

* `gaoptimset` 函数用于设置遗传算法的参数，包括种群大小、迭代次数和显示选项。
* `ga` 函数执行遗传算法优化，并返回最优解、最优值、退出标志和输出信息。
* `fun` 是目标函数，它是一个匿名函数，表示要优化的函数。
* `[x, fval, exitflag, output]` 分别表示最优解、最优值、退出标志和输出信息。
* `fprintf` 函数用于输出优化结果。

**参数说明：**

* `PopulationSize`：种群大小，即每次迭代中考虑的候选解的数量。
* `Generations`：迭代次数，即遗传算法运行的代数。
* `Display`：显示选项，可以设置为 `iter` 以在每次迭代后显示进度信息。
* `-10` 和 `10`：搜索空间的下界和上界。

**优化步骤：**

1. 定义目标函数。
2. 设置遗传算法参数。
3. 执行遗传算法优化。
4. 输出优化结果。

**扩展性说明：**

遗传算法还可以用于优化多目标函数。对于多目标优化问题，可以使用 `gamultiobj` 函数。此外，遗传算法还可以与其他优化算法相结合，形成混合算法，以提高优化效率。

# 4.1 多目标优化

在实际应用中，优化问题往往涉及多个目标，这些目标之间可能相互冲突或相互制约。多目标优化算法旨在解决此类问题，通过找到一组可行的解决方案，使所有目标函数都得到优化。

### 4.1.1 多目标优化原理

多目标优化算法的基本原理是通过进化过程寻找一组帕累托最优解。帕累托最优解是指对于任何一个目标函数，都不可能通过改善其他目标函数的值来进一步优化该目标函数。

### 4.1.2 NSGA-II算法

NSGA-II（非支配排序遗传算法 II）是一种经典的多目标优化算法，它通过以下步骤实现：

1. **初始化种群：**随机生成一组初始解。
2. **非支配排序：**将种群中的个体按照非支配关系排序。非支配个体是指没有其他个体同时优于它在所有目标函数上的值。
3. **拥挤距离计算：**计算每个个体的拥挤距离，拥挤距离表示个体周围其他个体的密度。
4. **选择：**根据非支配等级和拥挤距离，选择下一代的个体。非支配等级高的个体优先选择，拥挤距离大的个体优先选择。
5. **交叉和变异：**对选出的个体进行交叉和变异操作，产生新的个体。
6. **重复步骤2-5：**重复上述步骤，直到达到终止条件（例如，达到最大迭代次数或目标函数值收敛）。

### 4.1.3 MATLAB中的NSGA-II实现

MATLAB中提供了NSGA-II算法的实现，如下所示：

options = gaoptimset('PopulationSize', 100, 'Generations', 100, 'Display', 'iter');
[x, fval, exitflag, output] = gamultiobj(@myfun, nvars, [], [], [], [], lb, ub, [], options);

其中：

* `myfun`是目标函数，它返回一个包含多个目标函数值的向量。
* `nvars`是变量的数量。
* `lb`和`ub`是变量的下界和上界。
* `options`是遗传算法选项，包括种群大小、迭代次数和显示选项。

### 4.1.4 代码逻辑分析

此代码首先设置遗传算法选项，包括种群大小、迭代次数和显示选项。然后，它调用`gamultiobj`函数，该函数执行NSGA-II算法。`gamultiobj`函数返回一组帕累托最优解，存储在`x`变量中。`fval`变量包含目标函数值，`exitflag`变量指示算法是否成功终止，`output`变量包含其他信息，例如迭代次数和最佳解。

### 4.1.5 应用实例

多目标优化在许多实际应用中都有用，例如：

* **投资组合优化：**优化投资组合，以最大化收益并最小化风险。
* **工程设计：**优化工程设计，以满足多个性能指标，例如重量、强度和成本。
* **资源分配：**优化资源分配，以最大化效率和公平性。

# 5. MATLAB遗传算法在实际项目中的应用

### 5.1 供应链管理

遗传算法在供应链管理中有着广泛的应用，可以优化供应链的各个方面，包括：

- **库存管理：**遗传算法可以帮助企业优化库存水平，以最大限度地提高效率并减少成本。它可以通过模拟不同库存策略的影响来确定最佳库存策略。
- **物流规划：**遗传算法可以优化物流网络，以最小化运输成本和时间。它可以通过考虑多个因素，例如运输距离、交通状况和车辆容量，来确定最佳的运输路线和时间表。
- **采购管理：**遗传算法可以帮助企业优化采购流程，以获得最佳价格和质量。它可以通过考虑供应商的报价、交货时间和质量记录，来确定最佳供应商。

### 5.2 金融建模

遗传算法在金融建模中也有着广泛的应用，可以优化投资组合、风险管理和预测市场趋势。

- **投资组合优化：**遗传算法可以帮助投资者优化投资组合，以最大化收益并最小化风险。它可以通过模拟不同投资组合的影响来确定最佳的投资组合。
- **风险管理：**遗传算法可以帮助金融机构管理风险，例如信用风险和市场风险。它可以通过模拟不同风险情景的影响来确定最佳的风险管理策略。
- **市场预测：**遗传算法可以帮助金融分析师预测市场趋势，例如股票价格和汇率。它可以通过分析历史数据和考虑多个因素，例如经济指标和政治事件，来生成预测。

### 5.3 生物信息学

遗传算法在生物信息学中也有着重要的应用，可以分析基因数据、预测疾病风险和开发新药。

- **基因数据分析：**遗传算法可以帮助生物学家分析基因数据，以识别疾病相关的基因和突变。它可以通过模拟不同基因组合的影响来确定最有可能导致疾病的基因。
- **疾病风险预测：**遗传算法可以帮助医疗专业人员预测个体的疾病风险，例如癌症和心脏病。它可以通过考虑个体的基因、生活方式和环境因素，来生成风险评估。
- **新药开发：**遗传算法可以帮助制药公司开发新药，以治疗各种疾病。它可以通过模拟不同分子结构的影响来确定最有可能有效的新药。

# 6. MATLAB遗传算法的未来发展趋势

### 6.1 混合算法

遗传算法可以与其他优化算法相结合，形成混合算法，以提高优化效率和鲁棒性。例如：

- **粒子群优化（PSO）**：PSO算法基于鸟群觅食行为，具有较强的全局搜索能力。将PSO与遗传算法相结合，可以提高算法的收敛速度和优化精度。
- **模拟退火（SA）**：SA算法模拟金属退火过程，具有较强的局部搜索能力。将SA与遗传算法相结合，可以提高算法的解的质量和鲁棒性。

### 6.2 量子遗传算法

量子遗传算法（QGA）是一种将量子计算技术应用于遗传算法的算法。QGA利用量子比特和量子门进行运算，具有传统遗传算法无法比拟的并行性和搜索能力。QGA在解决大规模复杂优化问题方面具有广阔的应用前景。

### 6.3 遗传算法在人工智能中的应用

遗传算法在人工智能领域有着广泛的应用，例如：

- **神经网络训练**：遗传算法可以优化神经网络的权重和结构，提高神经网络的性能。
- **特征选择**：遗传算法可以从大量特征中选择最优特征子集，提高机器学习模型的精度和效率。
- **强化学习**：遗传算法可以优化强化学习中的策略，提高学习效率和决策质量。