揭秘MATLAB图像处理的秘密武器：图像增强技术大揭秘

# 1. 图像增强技术概述

图像增强技术是一类旨在改善图像视觉质量的处理技术，广泛应用于图像处理、计算机视觉和模式识别等领域。图像增强技术主要通过对图像像素值的调整或变换，增强图像的对比度、亮度、清晰度等视觉特征，从而提高图像的可读性和可理解性。

图像增强技术可以分为两大类：空间域图像增强和频域图像增强。空间域图像增强直接操作图像像素值，常用的方法包括灰度变换、直方图均衡化和局部对比度增强。频域图像增强则将图像转换为频域，通过滤波器设计和图像复原等技术进行增强。

# 2. 空间域图像增强

空间域图像增强是指直接对图像像素进行操作，以改善图像的视觉效果。它主要包括灰度变换、直方图均衡化和局部对比度增强。

### 2.1 灰度变换

灰度变换是对图像中每个像素的灰度值进行转换，以调整图像的亮度和对比度。

#### 2.1.1 线性灰度变换

线性灰度变换使用一个线性函数对图像像素的灰度值进行转换，形式为：

g(x, y) = a * f(x, y) + b

其中：

* `f(x, y)` 是原始图像的像素灰度值
* `g(x, y)` 是转换后的像素灰度值
* `a` 是斜率参数，控制图像的对比度
* `b` 是截距参数，控制图像的亮度

#### 2.1.2 非线性灰度变换

非线性灰度变换使用一个非线性函数对图像像素的灰度值进行转换，以产生更复杂的效果。常见的非线性灰度变换包括：

* **对数变换：** `g(x, y) = c * log(1 + f(x, y))`
* **幂律变换：** `g(x, y) = c * f(x, y)^γ`
* **分段线性变换：** 将图像的灰度范围划分为多个区间，并在每个区间内使用不同的线性函数进行转换

### 2.2 直方图均衡化

直方图均衡化是一种图像增强技术，通过调整图像的直方图分布来改善图像的对比度。

#### 2.2.1 直方图均衡化的原理

直方图均衡化的原理是将图像的直方图分布拉伸到整个灰度范围，使图像中各个灰度值的分布更加均匀。这样可以增加图像的对比度，使图像中的细节更加清晰。

#### 2.2.2 直方图均衡化的应用

直方图均衡化广泛应用于图像增强领域，包括：

* **医学图像增强：** 提高医学图像的对比度，便于诊断
* **遥感图像增强：** 增强遥感图像中地物特征的对比度
* **图像预处理：** 为后续图像处理任务（如边缘检测、目标识别）提供更好的输入

### 2.3 局部对比度增强

局部对比度增强是指对图像中的局部区域进行处理，以提高该区域的对比度。

#### 2.3.1 邻域平均滤波

邻域平均滤波是一种局部对比度增强技术，通过计算图像中每个像素周围邻域的平均灰度值来平滑图像。这可以消除图像中的噪声和模糊，同时保留图像的边缘和细节。

#### 2.3.2 锐化滤波

锐化滤波是一种局部对比度增强技术，通过强调图像中的边缘和细节来增强图像的清晰度。常见的锐化滤波器包括：

* **拉普拉斯滤波器：** `[0, -1, 0; -1, 4, -1; 0, -1, 0]`
* **Sobel滤波器：** `[1, 0, -1; 2, 0, -2; 1, 0, -1]`
* **Prewitt滤波器：** `[1, 0, -1; 1, 0, -1; 1, 0, -1]`

# 3. 频域图像增强

频域图像增强是一种基于图像傅里叶变换的图像增强技术。傅里叶变换将图像从空间域转换为频域，在频域中，图像的频率分量分布在不同的位置。通过对频域分量的处理，可以实现图像的增强。

### 3.1 傅里叶变换

傅里叶变换是一种数学变换，它将一个函数从时域（或空间域）转换为频域。对于图像，傅里叶变换将图像从空间域（像素值）转换为频域（频率分量）。

**3.1.1 傅里叶变换的原理**

一维傅里叶变换的公式为：

F(u) = ∫_{-\infty}^{\infty} f(x) e^{-i2πux} dx

其中：

* `f(x)` 是空间域的函数（图像）
* `F(u)` 是频域的函数（频率分量）
* `u` 是频率变量

傅里叶变换将图像中的每个像素值转换为一个复数，其中实部表示幅度，虚部表示相位。

**3.1.2 傅里叶变换的应用**

傅里叶变换在图像处理中有着广泛的应用，包括：

* 图像增强
* 图像去噪
* 图像复原
* 图像分析

### 3.2 滤波器设计

在频域图像增强中，滤波器用于选择性地增强或抑制图像中的特定频率分量。

**3.2.1 理想滤波器**

理想滤波器是一种理想化的滤波器，它可以完全通过或完全抑制指定的频率范围。理想低通滤波器的公式为：

H(u, v) =
    \begin{cases}
        1, & \text{if } u^2 + v^2 \leq D_0^2 \\
        0, & \text{otherwise}
    \end{cases}

其中：

* `H(u, v)` 是滤波器函数
* `D_0` 是截止频率

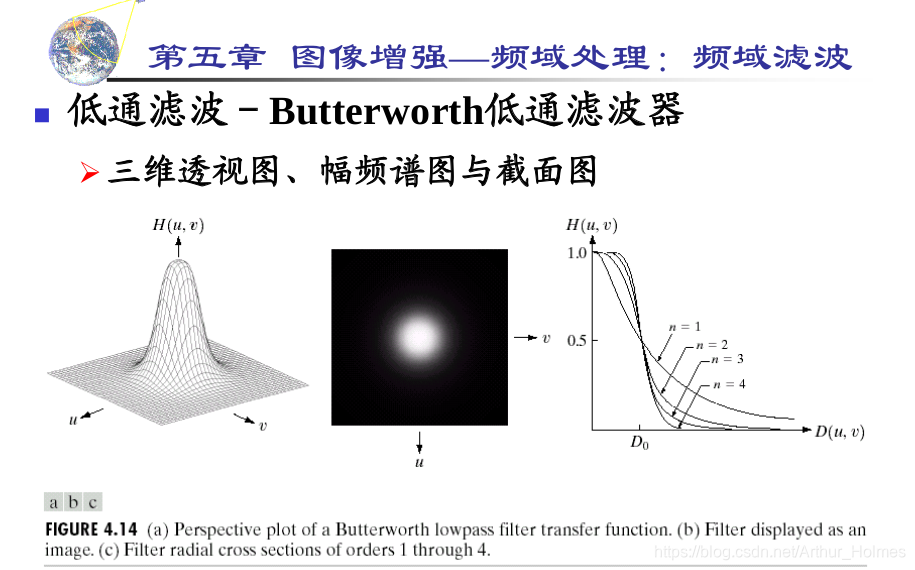
**3.2.2 巴特沃斯滤波器**

巴特沃斯滤波器是一种非理想滤波器，它在截止频率附近具有平滑的过渡带。巴特沃斯低通滤波器的公式为：

H(u, v) =
    \frac{1}{1 + \left(\frac{u^2 + v^2}{D_0^2}\right)^n}

其中：

* `n` 是滤波器的阶数

### 3.3 图像复原

图像复原是利用图像处理技术恢复图像中丢失或损坏的信息。

**3.3.1 维纳滤波**

维纳滤波是一种最优线性滤波器，它用于恢复受加性噪声影响的图像。维纳滤波器的公式为：

H(u, v) = \frac{S(u, v)}{S(u, v) + N(u, v)}

其中：

* `S(u, v)` 是原始图像的功率谱密度
* `N(u, v)` 是噪声的功率谱密度

**3.3.2 反卷积滤波**

反卷积滤波是一种非线性滤波器，它用于恢复受运动模糊影响的图像。反卷积滤波器的公式为：

g(x, y) = f(x, y) ⊗ h^{-1}(x, y)

其中：

* `g(x, y)` 是复原后的图像
* `f(x, y)` 是模糊的图像
* `h(x, y)` 是运动模糊核
* `⊗` 表示卷积运算

# 4. 基于小波变换的图像增强

### 4.1 小波变换

#### 4.1.1 小波变换的原理

小波变换是一种时频分析工具，它将信号分解成一系列称为小波的基函数。这些小波具有不同的频率和时间尺度，可以有效地捕捉信号的局部特征。

小波变换的数学表达式为：

$$W_f(a, b) = \int_{-\infty}^{\infty} f(t) \psi_{a, b}(t) dt$$

其中：

* $W_f(a, b)$ 是小波变换系数
* $f(t)$ 是待分解信号
* $\psi_{a, b}(t)$ 是小波基函数
* $a$ 是尺度参数，控制小波的频率
* $b$ 是平移参数，控制小波的时间位置

#### 4.1.2 小波变换的应用

小波变换广泛应用于图像处理、信号处理、语音处理等领域。在图像处理中，小波变换可以用于：

* 图像去噪
* 图像融合
* 特征提取
* 图像压缩

### 4.2 图像去噪

#### 4.2.1 小波软阈值去噪

小波软阈值去噪是一种基于小波变换的去噪算法。其基本原理是：将图像的小波系数与一个阈值进行比较，如果系数绝对值小于阈值，则将其置为零；否则，将系数减去阈值。

小波软阈值去噪算法的数学表达式为：

$$W_f'(a, b) = \begin{cases} W_f(a, b) - \tau, & \text{if } |W_f(a, b)| > \tau \\\ 0, & \text{otherwise} \end{cases}$$

其中：

* $W_f'(a, b)$ 是去噪后的小波系数
* $W_f(a, b)$ 是原始小波系数
* $\tau$ 是阈值

#### 4.2.2 小波硬阈值去噪

小波硬阈值去噪与小波软阈值去噪类似，但其将小于阈值的系数直接置为零，而不是减去阈值。

小波硬阈值去噪算法的数学表达式为：

$$W_f'(a, b) = \begin{cases} W_f(a, b), & \text{if } |W_f(a, b)| > \tau \\\ 0, & \text{otherwise} \end{cases}$$

### 4.3 图像融合

#### 4.3.1 小波融合算法

小波融合算法是一种基于小波变换的图像融合算法。其基本原理是：将待融合图像的小波系数进行加权平均，得到融合后的图像小波系数，再通过小波逆变换得到融合后的图像。

小波融合算法的数学表达式为：

$$W_f'(a, b) = \sum_{i=1}^n w_i W_i(a, b)$$

其中：

* $W_f'(a, b)$ 是融合后图像的小波系数
* $W_i(a, b)$ 是第 $i$ 幅图像的小波系数
* $w_i$ 是第 $i$ 幅图像的权重

#### 4.3.2 小波融合的应用

小波融合算法广泛应用于医学图像融合、遥感图像融合、多模态图像融合等领域。其优点在于：

* 能够有效地融合不同图像的互补信息
* 具有良好的抗噪声能力
* 能够保留图像的边缘和纹理信息

# 5.1 医学图像增强

### 5.1.1 医学图像增强的方法

医学图像增强是一种通过计算机技术处理医学图像，以提高图像的视觉质量和信息含量，从而辅助医学诊断和治疗的技术。常用的医学图像增强方法包括：

- **灰度变换：**调整图像的灰度值分布，以增强图像的对比度和亮度。
- **直方图均衡化：**通过调整图像的直方图，使图像的灰度值分布更加均匀，从而提高图像的对比度。
- **局部对比度增强：**通过邻域平均滤波或锐化滤波等技术，增强图像局部区域的对比度，突出图像中的细节。
- **频域滤波：**将图像转换为频域，并通过设计滤波器对图像进行滤波，以去除噪声或增强特定频率成分。
- **小波变换：**将图像分解为小波系数，并通过阈值去噪或融合等技术，增强图像的质量。

### 5.1.2 医学图像增强的应用

医学图像增强技术在医学领域有着广泛的应用，包括：

- **X 射线图像增强：**提高 X 射线图像的对比度和清晰度，以辅助骨骼、肺部和心脏等组织的诊断。
- **CT 图像增强：**增强 CT 图像的软组织对比度，以辅助肿瘤、血管和器官的诊断。
- **MRI 图像增强：**提高 MRI 图像的对比度和信噪比，以辅助脑部、脊髓和肌肉骨骼系统的诊断。
- **超声图像增强：**增强超声图像的清晰度和边界，以辅助胎儿、腹部和心脏的诊断。
- **内窥镜图像增强：**提高内窥镜图像的对比度和亮度，以辅助消化道、呼吸道和泌尿系统的诊断。

# 6.1 深度学习在图像增强中的应用

深度学习作为人工智能领域的一项突破性技术，在图像增强领域也发挥着越来越重要的作用。深度学习模型能够从大量图像数据中学习复杂的模式和特征，从而实现图像增强的各种任务。

### 6.1.1 深度学习图像增强算法

目前，深度学习在图像增强领域主要应用于以下算法：

- **生成对抗网络（GAN）**：GAN是一种生成式模型，能够生成逼真的图像。在图像增强中，GAN可以用来生成高分辨率图像、超分辨率图像以及修复损坏的图像。
- **卷积神经网络（CNN）**：CNN是一种专门用于处理图像数据的深度学习模型。在图像增强中，CNN可以用来执行图像去噪、图像锐化和图像超分辨率等任务。
- **自编码器（AE）**：AE是一种无监督学习模型，能够学习输入数据的潜在表示。在图像增强中，AE可以用来执行图像降噪和图像压缩等任务。

### 6.1.2 深度学习图像增强应用

深度学习图像增强技术在实际应用中有着广泛的应用，包括：

- **医学图像增强**：深度学习模型可以用来增强医学图像，提高诊断和治疗的准确性。例如，深度学习模型可以用来增强CT图像，提高肺结节检测的准确性。
- **遥感图像增强**：深度学习模型可以用来增强遥感图像，提高地物识别和分类的准确性。例如，深度学习模型可以用来增强卫星图像，提高土地利用分类的准确性。
- **计算机视觉**：深度学习图像增强技术在计算机视觉领域有着广泛的应用，例如目标检测、图像分割和人脸识别等。
- **自然语言处理**：深度学习图像增强技术也可以应用于自然语言处理领域，例如图像字幕生成和图像问答等。