实时推理中的神经网络优化：算法层面的考量

# 1. 实时推理与神经网络的交汇点

在现代信息技术中，实时推理正逐渐成为衡量智能系统性能的关键指标。与传统神经网络相比，实现实时推理不仅需要模型结构的创新，还需要优化算法的配合以及硬件技术的支持。实时推理与神经网络的交汇点正是在这一背景下显得尤为重要。本章将探索实时推理中所涉及的关键技术和挑战，以及它们是如何与神经网络相结合，发挥出最大效能的。

## 1.1 实时推理的定义与重要性

实时推理指的是计算机系统能够以足够快的速度进行决策，以满足实时或近实时操作的要求。在许多应用场景中，如自动驾驶汽车、视频监控和智能医疗等领域，实时推理能够提升用户体验和系统反应速度。

## 1.2 神经网络在实时推理中的角色

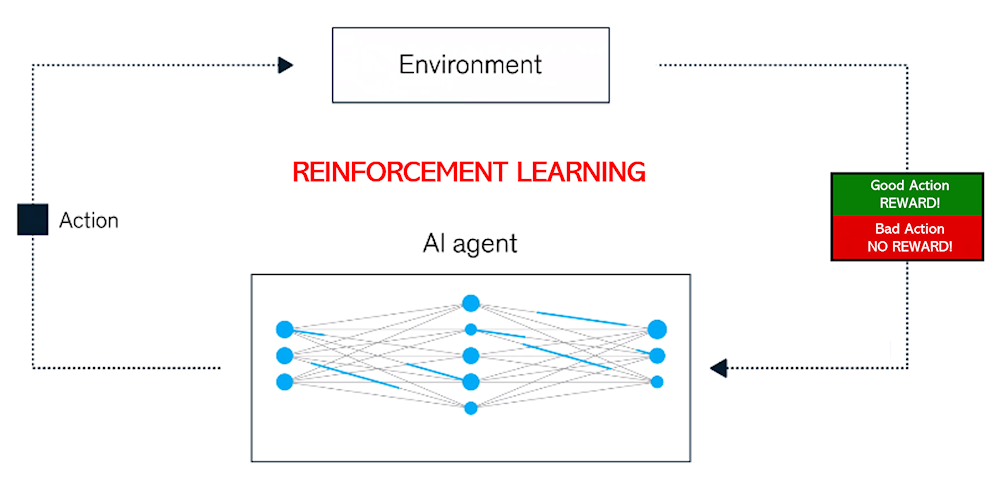
神经网络作为人工智能的核心技术之一，在实时推理中扮演着至关重要的角色。特别是在图像和语音识别、自然语言处理等领域，神经网络模型因其高准确性和学习能力，成为实现实时推理不可或缺的一部分。

## 1.3 实时推理面临的挑战

然而，实时推理面临着诸多挑战，例如模型的计算复杂度、硬件资源的限制以及实时性与准确性的平衡问题。为了克服这些挑战，研究人员和工程师们正在致力于优化神经网络的结构、训练算法以及硬件加速技术。

在接下来的章节中，我们将深入探讨如何通过优化神经网络和采用先进的硬件技术来克服实时推理的挑战，并实现高效、准确的智能决策。

# 2. 神经网络优化的理论基础

神经网络优化是机器学习领域中的一项核心课题，尤其在需要快速响应的实时推理任务中，神经网络的效率直接影响整个系统的性能。在优化神经网络时，研究者和工程师不仅需要关注网络结构的设计，还要深入了解各种优化算法的工作原理，以及如何合理地选择损失函数和正则化技术以避免过拟合。

### 2.1 神经网络结构概述

#### 2.1.1 常见的神经网络结构类型

神经网络的结构多种多样，根据不同的需求与应用场景，常见的结构包括但不限于全连接网络（FC）、卷积神经网络（CNN）、循环神经网络（RNN）、以及最近很热门的注意力机制网络（如Transformer）。每种结构都有其独特的特点和使用场景。

- **全连接网络（FC）**：这种结构的网络每层的每个神经元都与上一层的所有神经元相连。全连接网络通常用于处理结构化数据，它对数据的特征没有空间或时间的假设，因此在某些简单分类任务中效果很好。但它对于高维数据容易过拟合，并且参数众多，计算复杂度高。

- **卷积神经网络（CNN）**：CNN通过使用卷积层，有效地减少了网络参数的数量，并且能够提取到图像中的局部特征。这种网络特别适合处理图像和视频数据。CNN通过共享权重，使得网络对图像的位移、缩放、扭曲等变形具有一定的不变性。

- **循环神经网络（RNN）**：RNN的特殊之处在于它的网络结构能够处理序列数据。每个神经元不仅与前一层相连，还与自身相连，这使得网络可以处理具有时间依赖关系的数据，如文本或时间序列数据。LSTM和GRU是RNN的两种变体，它们通过特殊的门控机制解决了RNN在长序列上的梯度消失问题。

- **注意力机制网络（如Transformer）**：注意力机制允许模型在处理序列数据时，对不同部分赋予不同的关注权重。Transformer模型就是以这种机制为核心，它抛弃了传统循环层结构，实现了并行处理并大幅提升了长序列数据处理的效率。目前，在自然语言处理（NLP）领域，Transformer模型已经广泛应用。

每种网络结构都有其适用的场景，例如，对于大规模图像识别任务，CNN通常是首选；而在处理长度不定的文本时，Transformer类模型则更为合适。了解每种网络结构的特点，可以帮助我们更好地为特定任务选择或设计网络。

#### 2.1.2 各结构在实时推理中的优劣分析

在实时推理的场景下，上述网络结构各有优劣，选择合适的神经网络结构需要考虑推理速度和准确性的平衡。

- **全连接网络（FC）**：由于其结构简单，计算速度快，全连接网络可以较快地进行推理。然而，由于参数数量巨大，它通常不适合内存受限的实时推理系统。

- **卷积神经网络（CNN）**：CNN由于其参数共享的特性，相较于FC网络参数较少，且因为卷积操作可以高度优化（例如使用GPU加速），在实时推理中可以实现很快的速度。CNN结构也特别适用于图像和视频分析任务。

- **循环神经网络（RNN）**：RNN的计算通常涉及序列数据，这种逐个时间步的计算方式限制了其推理速度。但在处理短序列数据时，RNN依然是一个不错的选择。

- **注意力机制网络（如Transformer）**：Transformer模型虽然在训练时计算量大，但是在进行推理时，由于其并行处理的能力，可以实现非常快的处理速度。特别适合在具有大规模数据和强计算资源支持的场景下使用。

在实时推理的实践中，模型轻量化是一个常见的趋势。一些轻量级的CNN变体，如MobileNet、ShuffleNet等，以及为RNN和Transformer设计的轻量级版本，如LSTM的变体，都是为了优化速度和准确性的权衡设计的。

### 2.2 优化算法的理论分类

优化算法是训练神经网络不可或缺的一环，通过梯度下降及其变种、二阶导数优化方法以及非梯度优化方法，研究者可以找到参数空间中损失函数的极值点，从而使得模型在训练数据上表现良好。

#### 2.2.1 梯度下降及其变种

梯度下降是一种广泛使用的优化算法，它通过迭代地沿着损失函数的梯度方向更新参数以最小化损失函数。基本的梯度下降算法简单直观，但在实际应用中往往会遇到一些困难，比如学习速率的选择、局部最小值问题等。

- **批量梯度下降（Batch Gradient Descent）**：这种算法在每次更新中使用整个训练集来计算梯度。它的优点是每次更新都朝着正确的方向前进，但缺点是速度慢且占用大量内存。

- **随机梯度下降（Stochastic Gradient Descent, SGD）**：与批量梯度下降不同，随机梯度下降每次只使用一个样本或一小批样本来更新参数。这使得SGD计算效率更高，但缺点是更新过程中的噪声较大，可能会导致训练过程震荡。

- **小批量梯度下降（Mini-batch Gradient Descent）**：小批量梯度下降是批量梯度下降和随机梯度下降的折中方案。它每次使用一小批样本来计算梯度，这样既保留了SGD的内存效率又具有一定的计算稳定性。

梯度下降变种算法不断演进，例如动量法（Momentum）、自适应学习率算法如Adam和Adagrad，它们试图解决标准SGD在面对非凸函数时收敛速度慢、容易陷入局部最小值等问题。

#### 2.2.2 基于二阶导数的优化算法

二阶导数优化算法通常涉及Hessian矩阵，它包含了目标函数关于参数的二阶导数。二阶导数提供了函数曲率的信息，理论上可以提供更精确的搜索方向。

- **牛顿法（Newton's Method）**：牛顿法利用二阶导数（Hessian矩阵）来优化目标函数。它相对于梯度下降算法的一个主要优势在于收敛速度，但在实际应用中，由于需要计算和存储Hessian矩阵，牛顿法可能不太适合大规模神经网络优化。

- **拟牛顿法（Quasi-Newton Methods）**：拟牛顿法试图克服牛顿法中的Hessian矩阵计算的复杂性。它们通过迭代地更新Hessian矩阵的逆矩阵来近似牛顿法的效果，而不需要精确计算Hessian矩阵。

二阶导数方法虽然在理论上具有优势，但由于内存和计算效率问题，在处理大型神经网络时往往会受到限制。

#### 2.2.3 非梯度优化方法

在很多实际应用中，尤其是在网络结构非常复杂的情况下，计算梯度可能是非常困难的，或者根本不可能。这时，非梯度优化方法就显得尤为重要。

- **遗传算法（Genetic Algorithms）**：遗传算法是一种模拟自然选择过程的优化算法。通过模拟自然进化中的遗传机制，不断迭代地选择、交叉和变异参数集合，逐步逼近最优解。

- **模拟退火（Simulated Annealing）**：模拟退火是受物理退火过程启发而来的优化方法，通过随机搜索和“冷却”过程（降低搜索空间的范围）来跳出局部最小值，增加找到全局最优解的概率。

非梯度优化方法不依赖于梯度信息，这使得它们在某些特定问题上特别有用，尤其是在梯度难以计算或者不连续的优化问题中。然而，由于这些方法通常计算量大且收敛速度慢，它们往往作为梯度下降方法的一个补充。

### 2.3 损失函数与正则化技术

损失函数和正则化技术是神经网络优化中不可或缺的组成部分，它们不仅影响训练过程，还影响模型在未知数据上的泛化能力。

#### 2.3.1 损失函数的作用和选择

损失函数（或目标函数、成本函数）衡量了模型预测值和实际值之间的差异。在训练过程中，模型通过最小化损失函数来学习数据的分布。不同的问题和任务需要选择不同的损失函数。

- **均方误差（MSE）**：当处理回归问题时，均方误差是一个常见的损失函数。它通过计算预测值和实际值差值的平方来衡量模型性能。

- **交叉熵损失（Cross-Entropy Loss）**：在处理分类问题时，交叉熵损失函数是更为常见的选择。它衡量的是模型输出