神经网络量化技术：降低资源消耗，实现实时推理

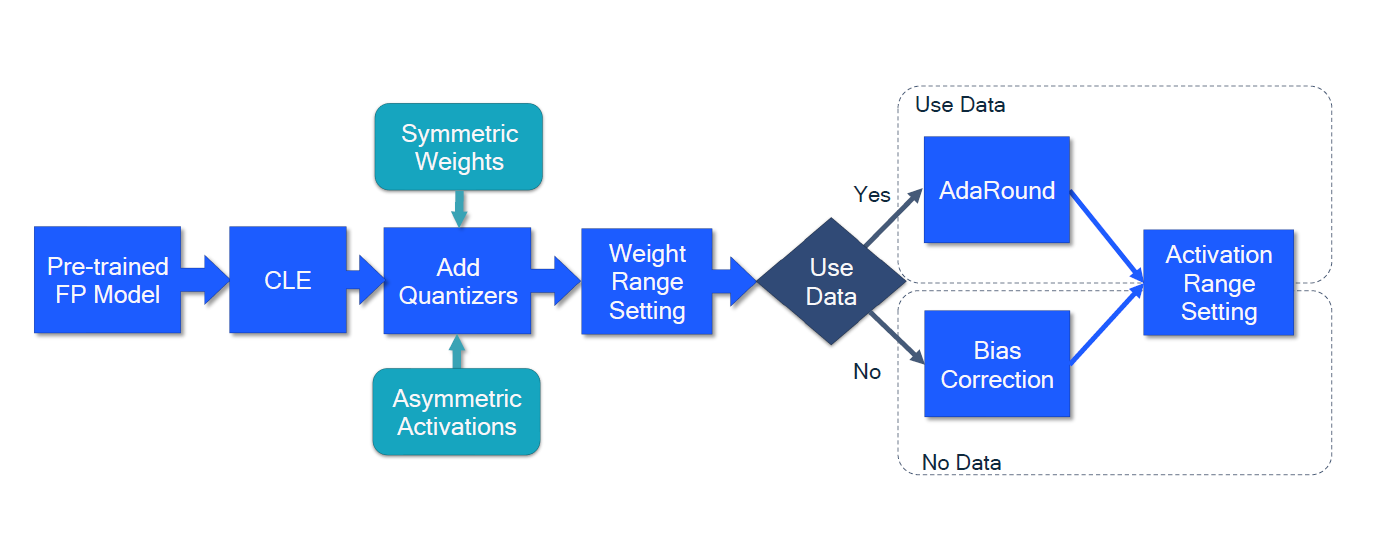
# 1. 神经网络量化技术概述

神经网络量化技术是深度学习领域的一项关键技术，通过将神经网络中的参数和激活值从浮点数转换为低精度的数据类型（例如定点数），从而达到减少模型大小、加快推理速度、降低计算资源消耗的目的。这种技术在部署深度学习模型到资源受限的设备上，比如移动设备、嵌入式系统和物联网设备，显示出其独特的优势。在本文中，我们将探讨量化技术的基础理论、实践技巧以及面临的挑战和未来的发展趋势，帮助读者全面深入理解这一技术，并为实际应用提供指导。

# 2. 量化理论基础

## 2.1 量化技术的数学原理

### 2.1.1 神经网络参数的数据类型

神经网络中的参数通常以浮点数形式表示，以保持在训练过程中的高精度。然而，浮点数格式需要更多的存储空间和计算资源，这对于大规模神经网络模型来说是不切实际的。为了优化这些资源需求，量化技术通过减少数据表示的位宽来转换这些浮点数参数到更紧凑的数据类型。例如，从32位浮点数（FP32）转换为8位整数（INT8）。这种转换使得模型大小、内存占用和运算速度得到显著改进，同时也带来了精度损失。

### 2.1.2 数据类型转换的方法和精度损失

量化参数涉及舍入和缩放。缩放因子和零点是转换过程中的关键参数，用于将浮点数映射到整数，并在反量化时将其转换回原来的范围。尽管舍入误差和缩放不准确会导致精度损失，但通过适当的选择缩放因子和零点，可以在保持精度的同时最小化这种损失。

# 以Python示例代码来演示FP32到INT8的转换过程
import numpy as np

# 假设我们有以下浮点数参数张量
fp32_tensor = np.array([0.5, 1.0, 1.5, 2.0], dtype=np.float32)

# 量化参数：最小值、最大值、目标位宽
min_val = np.min(fp32_tensor)
max_val = np.max(fp32_tensor)
num_bits = 8  # 量化到INT8

# 缩放因子计算
scale = (max_val - min_val) / (2**num_bits - 1)

# 零点计算
zero_point = -min_val / scale

# 量化操作
int8_tensor = np.round(fp32_tensor / scale) + zero_point
int8_tensor = np.clip(int8_tensor, 0, 2**num_bits-1)  # 限制到INT8的有效范围

# 执行逻辑说明
# 首先，根据参数的最大值和最小值计算缩放因子，然后计算零点。
# 接着，利用缩放因子将浮点数转换为整数，并加上零点来得到最终的量化值。
# 为了防止溢出，结果会被限制在INT8的有效范围内。

## 2.2 量化方法分类

### 2.2.1 权重量化和激活量化

权重量化涉及将网络权重参数从浮点数转换为定点数。激活量化则是针对每一层的输出进行量化处理。两者都是优化网络性能的重要方法。权重量化通常在训练阶段结束后进行，而激活量化可以在训练过程中或者推理时执行。

### 2.2.2 量化级别和精度

量化级别指的是数据在量化后表示的精度，通常分为8位、16位等。精度越高，表示的数值范围越广，但相应的存储和计算要求也越高。选择合适的量化级别是优化性能与精度平衡的关键。

### 2.2.3 精度校准策略

在量化过程中，需要校准量化参数以保持模型的预测能力。常见的策略包括最小最大值校准、百分位数校准和全局校准。校准策略的选择依赖于模型的特性和应用需求。

## 2.3 量化对性能的影响

### 2.3.1 量化对模型大小的影响

通过量化，可以显著减小模型的存储大小，这对移动设备和边缘计算场景至关重要。例如，一个FP32的模型可能大小为100MB，而INT8量化后可能降低到25MB，极大减少了存储空间的需求。

### 2.3.2 量化对计算资源的节约

由于量化后的数据类型占用的空间更小，CPU和GPU可以更高效地处理这些数据。此外，量化也有助于利用专门的硬件加速器，这些加速器针对低精度的数值运算进行了优化。因此，量化可以显著减少推理时间，提高运算效率。

graph LR
    A[原始模型] --> B{量化过程}
    B --> C[量化模型]
    C --> D[存储空间]
    C --> E[推理速度]
    D -->|减小| F[模型大小]
    E -->|加快| G[推理效率]

以上章节的内容从量化技术的基本理论出发，对数据类型转换、量化方法分类和性能影响进行了详细的介绍。通过量化可以有效地优化深度学习模型的资源占用和推理效率，为实际部署提供了理论依据。在下一章中，我们将深入探讨量化实践的技巧和工具。

# 3. 量化实践技巧

## 3.1 量化工作流程

在开始量化工作流程之前，重要的是理解量化不仅仅是一个单一的步骤，而是一系列步骤，这些步骤需要密切配合以确保最终模型在精度损失最小化的同时获得性能提升。这个过程通常包括模型训练与验证、量化敏感性分析和量化与剪枝的结合。

### 3.1.1 模型训练与验证

在进行量化之前，首先需要训练并验证一个基线模型。这个模型将作为量化前后性能对比的基准。训练过程需要精心调整，确保模型在训练数据集上达到了满意的性能。验证则是在一个独立的测试集上完成的，用于评估模型在未见过的数据上的泛化能力。

# 示例代码：使用PyTorch训练一个简单的卷积神经网络（CNN）模型

import torch
import torch.nn as nn
import torch.optim as optim

# 定义模型结构
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3, stride=1)
        self.fc = nn.Linear(32*24*24, 10)  # 假设输入图像大小为28*28

    def forward(self, x):
        x = torch.relu(self.conv(x))
        x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x

# 实例化模型、损失函数和优化器
model = SimpleCNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)

# 训练模型（这里仅为示例代码，省略了实际训练数据加载和训练循环）
# ...

在上述代码中，我们定义了一个简单的CNN模型，包含了卷积层和全连接层，并使用SGD优化器进行训练。量化之前确保模型精度是量化实践的第一步。

### 3.1.2 量化敏感性分析

量化敏感性分析是确定哪些层或参数对量化最敏感的过程。敏感性分析有助于决定哪些部分需要更细致的量化策略，或者可能需要剪枝来减少量化损失。通常，分析的方法包括逐层计算量化前后的精度差异。

# 示例代码：计算模型的敏感性分析

def sensitivity_analysis(model):
    layer_sensitivity = {}
    for name, param in model.named_parameters():
        q_param = torch.quantize_per_tensor(param, 0.1, 0, 0, torch.qint8)
        # 量化模拟，此处省略反量化和比较精度的代码
        # ...
        sensitivity = # 某种度量量化后精度下降的方法
        layer_sensitivity[name] = sensitivity
    return layer_sensitivity

# 计算模型各层的量化敏感性
sensitivity = sensitivity_analysis(model)
print(sensitivity)

### 3.1.3 量化与剪枝的结合

为了优化最终模型的性能，量化通常与剪枝技术结合使用。剪枝技术可以移除冗余的神经元或连接，以降低模型复杂度，并且可以在某些情况下增加量化后的模型精度。

# 示例代码：简单剪枝函数，移除低于某个阈值的权重

def prune_weights(model, threshold):
    for name, param in model.named_parameters():
        mask = torch.abs(param) > threshold
        model._modules[name].data = model._modules[name].data[mask]
    return model

# 应用剪枝
pruned_model = prune_weights(model, threshold=0.01)

结合量化和剪枝的策略可以提升模型的压缩比例和推理速度，同时尝试最小化精度损失。

## 3.2 量化工具和框架

目前，许多开源框架已经提供了量化工具。选择合适的量化工具对于成功实施量化非常关键。在本小节中，我们将分析并比较流行的量化工具，并分析框架内建量化支持的细节。

### 3.2.1 开源量化工具的比较和选择

在选择量化工具时，需要考虑多个因素，如框架兼容性、量化精度、支持的量化级别、易用性等。以下是几个流行的量化工具及其特点的比较：

| 工具 | 描述 | 兼容性 | 量化级别 | 易用性 |
| --- | --- | --- | --- | --- |
| TensorRT | NVIDIA提供，专