现代控制理论数字仿真：习题解答及仿真实践手册


# 摘要
本文系统地探讨了现代控制理论在数字仿真中的基础和实践应用。首先介绍了控制系统建模的基本概念和方法，包括数学模型的建立和系统描述。随后，文章深入分析了系统时域和频域分析的关键特性及稳定性判据。在此基础上，本文详细讨论了数字仿真技术及其软件工具，突出了MATLAB/Simulink等工具在仿真操作中的技巧和优势。此外，本文还对经典控制理论和现代控制理论的仿真实践进行了深入研究，包括PID控制器、状态空间控制以及最优控制理论，并通过仿真案例分析展示了理论与实践的结合。最后，文章提供了针对不同控制理论的习题解答与案例分析，以加深读者对仿真技术和控制理论应用的理解。

# 关键字
控制理论；数字仿真；系统建模；状态空间；PID控制；最优控制；模型预测控制

参考资源链接：[现代控制系统（第十二版）谢红卫翻译习题解答指南](https://wenku.csdn.net/doc/3x2ahpqrky?spm=1055.2635.3001.10343)
# 1. 现代控制理论数字仿真的基础

## 1.1 数字仿真的意义与作用

数字仿真作为一种计算机辅助设计工具，在现代控制理论研究和工程应用中扮演了至关重要的角色。它允许工程师在不实际构建物理系统的情况下对系统进行测试和优化，这不仅可以节省成本，还能在系统开发过程中避免潜在的风险。通过数字仿真，可以对控制系统的性能进行全面分析，包括稳定性、响应速度、抗干扰能力等方面，为控制策略的制定提供了科学依据。

## 1.2 控制系统的数学描述

控制系统可以通过数学模型来描述，主要包括连续时间系统的微分方程和离散时间系统的差分方程。微分方程可以表达系统的动态行为，其中状态空间模型是现代控制理论中广泛采用的一种形式。状态空间模型通过状态变量的集合来完整地描述系统状态，便于应用计算机进行仿真分析。通过系统描述和微分方程的建立，工程师能够运用数学工具进行深入的理论分析和设计工作。

## 1.3 数字仿真的基本流程

数字仿真的基本流程通常包括建模、求解、分析和验证四个步骤。建模是将实际问题抽象成数学模型；求解是运用数值方法对模型进行求解；分析是对求解结果进行解读，提取出有用的信息；验证是将仿真结果与实验或者理论结果进行对比，以确保仿真的准确性和可靠性。通过这一系列流程，工程师可以在控制系统的开发周期中，实现高效的设计迭代和优化。

# 2. 控制系统建模与分析

控制系统建模与分析是理解系统性能与行为的基石。无论是在工程领域还是在理论研究中，一个精确的数学模型都是设计控制策略和分析系统动态的关键。在本章中，我们将探讨控制系统建模与分析的各个方面，包括数学模型的建立、时域分析、以及频域分析等。

## 2.1 数学模型的建立

### 2.1.1 系统描述和微分方程

控制系统的基本组成部分包括输入、输出、以及系统的动态特性。为了建立数学模型，首先需要对系统进行准确的描述。这通常涉及到识别系统的状态变量、控制输入、以及系统的输出。系统描述的一个重要工具是微分方程，它可以用来表达系统内部的状态变量如何随时间变化，以及这些变量如何受到控制输入和外部干扰的影响。

在控制系统中，微分方程可以是线性的也可以是非线性的，常微分方程或偏微分方程。对于线性时不变系统，常用的微分方程形式是拉普拉斯变换后的传递函数。对于更复杂的系统，例如非线性系统或时变系统，可能需要使用状态空间模型。

### 2.1.2 状态空间模型的构建

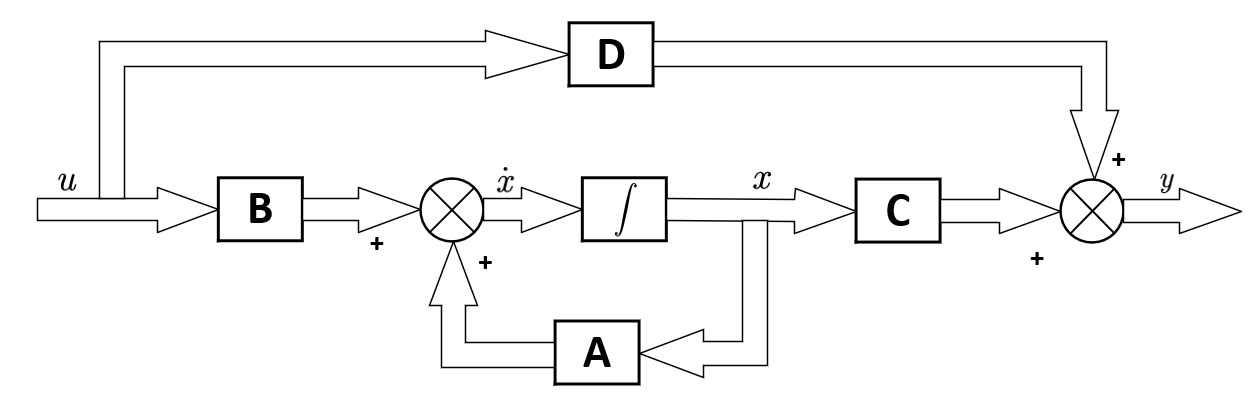
状态空间模型是控制系统分析中的一个核心概念，它由一组状态方程描述系统内部状态的动态行为。在状态空间模型中，系统的内部状态被表示为状态向量，系统的动态特性由状态方程描述，而系统的输出则由输出方程给出。状态空间模型的一般形式可以表示如下：

- 状态方程：x(t) = Ax(t) + Bu(t) + Ew(t)
- 输出方程：y(t) = Cx(t) + Du(t) + Fw(t)

在这里，x(t)是状态向量，u(t)是控制输入向量，y(t)是输出向量，w(t)是外部干扰向量。矩阵A、B、C、D、E和F分别代表系统的动态矩阵、输入矩阵、输出矩阵、直接传递矩阵、干扰矩阵和干扰传递矩阵。

构建状态空间模型通常需要对系统有深入的理解，并将物理现象转化为数学表达式。这涉及到对系统结构的分析和简化，以及对系统参数的测量或估计。状态空间模型不仅能够描述系统的线性特性，也能描述非线性特性，使得它成为分析和设计复杂系统时的首选。

## 2.2 系统的时域分析

### 2.2.1 稳态与瞬态特性分析

时域分析侧重于系统响应随时间的变化情况。稳态特性指的是系统经过足够长时间后的行为，而瞬态特性则描述系统从初始状态到稳态之间的动态变化过程。

稳态分析主要关心系统的长期行为，例如在阶跃输入或周期输入下的输出响应。稳态误差是衡量系统稳态特性的一个重要指标，它描述了系统输出与期望输出之间的差异。瞬态分析则关注系统达到稳态前的动态特性，包括上升时间、峰值时间、超调量以及调整时间等性能指标。

### 2.2.2 响应曲线与性能指标

响应曲线是系统动态特性的直观表示。最常用的是阶跃响应曲线，它可以展示系统在受到阶跃输入时的输出变化。通过阶跃响应曲线，可以直观地观察到系统的瞬态特性，如超调、振荡等。其他类型的响应曲线包括脉冲响应、正弦响应等，它们用于分析系统对不同输入信号的响应。

性能指标是评价系统响应质量的量化指标。例如，对于阶跃响应，上升时间（从输出开始变化到输出达到最终值的90%所需时间）是一个重要的性能指标。峰值时间（从输出开始变化到输出达到第一个峰值所需时间）以及超调量（输出超过最终值的最大量）是描述系统瞬态特性的性能指标。

通过这些响应曲线和性能指标，工程师可以判断系统是否满足设计要求，是否需要进一步调整控制策略或系统参数。

## 2.3 系统的频域分析

### 2.3.1 频率响应函数与Bode图

频域分析关注系统对不同频率输入信号的响应特性。频率响应函数描述了系统输出与输入信号频率之间的关系。最常见的频率响应函数表示方式是Bode图，它包括幅度图和相位图。幅度图表示了系统增益随频率变化的情况，而相位图则表示了系统相位延迟随频率的变化情况。

在频域分析中，系统稳定性的判断主要依据Nyquist稳定性准则。根据系统的开环传递函数绘制Nyquist图，如果该曲线不包围(-1,0)点，则系统是稳定的。此外，频域分析还涉及共振频率和带宽的概念，它们可以指示系统的动态特性和信号处理能力。

### 2.3.2 极点与稳定性判据

在频域分析中，系统极点的位置对系统稳定性有着决定性的影响。一个线性时不变系统的极点是其传递函数分母多项式的根。如果一个系统的所有极点都位于复平面的左半部分，则该系统是稳定的。系统稳定性的另一种判断方法是利用Routh-Hurwitz准则或者根轨迹分析法。

Routh-Hurwitz准则通过构建Routh表来判断系统的极点位置，从而得出系统是否稳定的结论。根轨迹分析法则通过在复平面上绘制根轨迹来直观地展示系统极点随系统增益变化的情况。

这些稳定性判据是控制系统设计和分析中不可或缺的工具，它们帮助工程师在设计阶段预防可能的不稳定现象。

本章节通过建立数学模型，分析系统时域和频域特性，为后续章节中控制系统的设计和仿真提供了理论基础。通过本章的介绍，控制系统工程师可以建立精确的模型，并对系统的动态行为进行深入分析。这些知识构成了现代控制理论中仿真实践和优化策略的基础。

# 3. 数字仿真技术与软件工具

数字仿真技术已经深入到控制系统的各个环节，它不仅加速了理论研究到实际应用的转化，还提高了工程设计的效率与准确性。在这一章节中，我们将深入了解数字仿真技术的基本原理，并探索用于仿真的软件工具。我们还将探讨如何有效地操作这些工具以构建模型、设置参数、分析结果以及进行后处理。通过本章节的深入解析，读者将掌握仿真工具的使用技巧，以及如何利用这些工具解决实际问题。

## 3.1 数字仿真的基本原理

数字仿真通过计算设备的数值计算来模拟物理过程，这需要使用到特定的数学模型和算法。数字仿真技术的关键在于如何通过离散的时间序列来近似连续的过程。

### 3.1.1 离散化方法和误差分析

离散化是指将一个连续的数学模型转化成可以通过计算机处理的离散模型。在控制系统仿真中，常见的离散化方法包括：

- 向前差分法
- 向后差分法
- 中心差分法
- 四阶龙格-库塔法

这些方法的选择对于仿真结果的准确性有着重要影响，因为不同方法具有不同的截断误差。例如，中心差分法的截断误差较小，适合需要较高精度的应用场合。而在实时系统中，由于计算速度的限制，我们可能倾向于使用截断误差相对较大但计算速度更快的方法，如向前差分法。

**代码块示例：** 使用不同离散化方法的比较

% 定义连续系统方程
continous_sys = @(t, x) -2*x;

% 时间跨度和步长
tspan = [0, 10];
h = 0.1;  % 步长

% 向前差分法
x_Forward = x0;
f