控制系统状态估计与容错控制：习题解答与实践案例精编


# 摘要
本文系统地探讨了控制系统状态估计和容错控制的理论基础与应用实践。首先，介绍了状态估计的基础知识，包括数学模型的构建和滤波算法的选择，分析了卡尔曼滤波技术以及扩展卡尔曼滤波与粒子滤波方法。随后，深入分析了容错控制的原理、结构及控制器设计，并对故障检测、隔离技术与系统可靠性和鲁棒性进行了性能分析。文章还探讨了智能诊断与自适应容错控制在复杂系统中的应用，并分析了智能控制系统在工业4.0中的角色以及面临的新挑战。最后，展望了控制系统状态估计与容错控制的未来发展方向，强调了人工智能技术在其中的重要作用。

# 关键字
状态估计；容错控制；卡尔曼滤波；故障检测；自适应控制；人工智能

参考资源链接：[现代控制系统（第十二版）谢红卫翻译习题解答指南](https://wenku.csdn.net/doc/3x2ahpqrky?spm=1055.2635.3001.10343)
# 1. 控制系统状态估计基础

控制系统状态估计是构建现代智能控制系统不可或缺的一部分，旨在实时准确地确定系统的内部状态。在本章中，我们将从控制系统状态估计的基本概念出发，理解其在系统监控与控制中的重要性，并初步探讨如何通过数学建模和算法选择来实现有效的状态估计。

## 1.1 状态估计的重要性

控制系统中状态估计的重要性在于为决策提供准确的系统内部状态信息，这是确保系统稳定运行和优化控制策略的前提。缺乏准确的状态信息可能导致控制失效，增加系统的不确定性，甚至在关键应用中引起安全事故。

## 1.2 状态估计的应用场景

状态估计广泛应用于各类控制系统，包括航空航天、工业自动化、智能交通、能源管理系统等。它能够帮助我们理解和预测系统行为，从而提高系统的性能和可靠性。

## 1.3 状态估计的基本方法

基本的状态估计方法包括但不限于最小二乘法、卡尔曼滤波、扩展卡尔曼滤波和粒子滤波等。这些方法各有优势和局限性，选择合适的方法需要根据实际应用需求和系统特性来决定。

通过本章的学习，读者将获得对控制系统状态估计基本概念的理解，并为深入学习后续章节中状态估计的理论与实践打下坚实的基础。

# 2. 状态估计理论详解与实践

## 2.1 状态估计的数学模型

在控制系统中，状态估计是核心组成部分，它允许系统从不完整的测量和不精确的模型中估计系统的内部状态。为了进行有效的状态估计，首先需要建立两个关键的数学模型：系统模型与观测模型。

### 2.1.1 系统模型与观测模型的建立

系统模型描述了系统状态随时间的动态演变，通常用状态空间表示法来描述。假设系统的状态向量为 x(t)，控制输入为 u(t)，我们可以用以下的微分方程来描述系统模型：

graph LR
A[系统初始状态] -->|状态方程| B[系统状态演变]
B -->|控制输入 u(t)| C[动态系统输出]

状态方程可以表示为：

x(t) = f(x(t), u(t), w(t))

其中，w(t)表示过程噪声，它模拟了模型无法预测的随机扰动。

观测模型则描述了系统状态与可用测量之间的关系。当存在观测向量 z(t) 和测量噪声 v(t) 时，观测模型可以表示为：

z(t) = h(x(t), v(t))

其中，h 表示观测函数。

### 2.1.2 概率模型与滤波算法选择

为了将噪声模型纳入考虑范围，可以使用概率模型来描述系统模型和观测模型。在概率模型下，系统状态和观测值被视为随机变量，并且具有相应的概率分布。

滤波算法的选择取决于概率模型的具体形式和系统的先验知识。例如，如果系统噪声和测量噪声可以假定为高斯分布，并且系统模型是线性的，那么线性高斯模型是适用的，卡尔曼滤波是这类模型的理想选择。

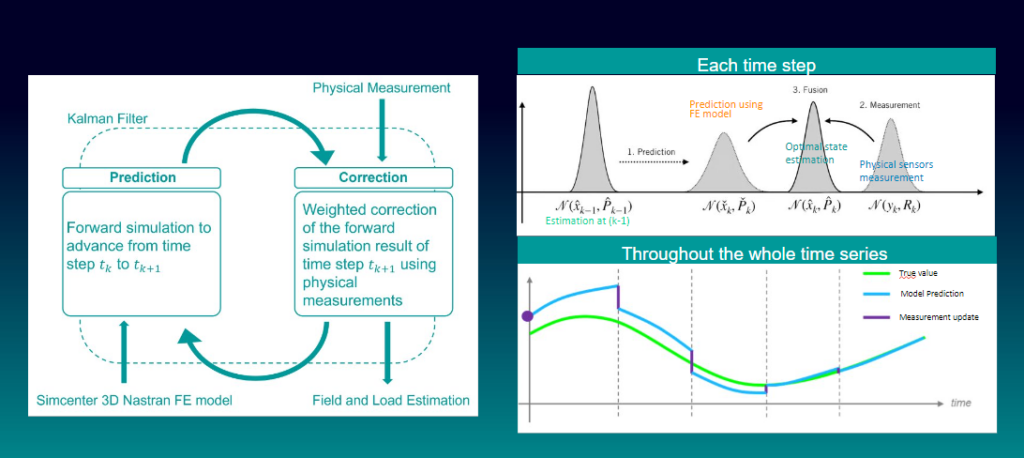
### 2.1.2.1 卡尔曼滤波

卡尔曼滤波是状态估计中最著名的算法之一，它为线性系统的状态估计提供了一种最优解。算法的基本步骤如下：

初始化：
    x(0|0) = E[x(0)]     # 初始状态估计
    P(0|0) = E[ (x(0) - x(0|0))(x(0) - x(0|0))' ] # 初始估计误差协方差

预测：
    x̂(k|k-1) = F(k)x̂(k-1|k-1) + B(k)u(k) + w(k)
    P(k|k-1) = F(k)P(k-1|k-1)F'(k) + Q(k)

更新：

K(k) = P(k|k-1)H'(k)[H(k)P(k|k-1)H'(k) + R(k)]^(-1)
x̂(k|k) = x̂(k|k-1) + K(k)[z(k) - H(k)x̂(k|k-1)]
P(k|k) = (I - K(k)H(k))P(k|k-1)

在上述公式中，x̂(k|k-1)表示在时刻 k 的预测状态，x̂(k|k)表示更新后的状态估计。P 表示估计误差的协方差，F 是系统矩阵，H 是观测矩阵，Q 是过程噪声的协方差，R 是测量噪声的协方差。K 是卡尔曼增益，它决定了观测数据对于状态估计更新的影响权重。

卡尔曼滤波具有很多变种，包括扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF），它们被用于处理非线性系统。

通过本章节的介绍，我们了解了状态估计的数学模型和卡尔曼滤波算法。在下一节中，我们将探讨更多的状态估计方法，包括扩展卡尔曼滤波和粒子滤波等。

# 3. 容错控制的理论与方法

## 3.1 容错控制的原理与结构

### 3.1.1 容错控制的基本概念和框架

容错控制系统是一种能够在组件发生故障时仍然维持控制性能的系统。容错控制的设计要求系统在遭遇部分硬件或软件故障时，仍能继续操作或至少在降级模式下操作，同时保证系统性能不会大幅下降。容错控制的核心在于其“冗余”设计，这包括硬件冗余、时间冗余、信息冗余或控制冗余等。

容错控制系统的基本框架由以下几个主要部分组成：
1. **传感器**：检测系统行为并反馈信号。
2. **执行器**：根