控制系统设计优化：谢红卫翻译版习题解析及优化策略全览


# 摘要
本文系统地概述了控制系统设计优化的各个方面，包括基础理论、系统性能指标、设计方法、习题解析、优化策略以及案例研究。首先介绍了控制系统的数学模型和性能指标，然后分析了控制系统设计的基本方法，如PID控制和鲁棒控制策略。接着，文章探讨了控制器设计与仿真方法，并通过习题解析来加深理解。第四章重点讲述了控制器参数优化和系统结构的优化设计，以及实时性能优化技术。案例研究部分提供了工业控制系统和智能控制系统的实际应用，最后对控制系统设计的未来展望与挑战进行了分析，包括新兴技术的融合潜力以及跨学科技术创新的需求。

# 关键字
控制系统；数学模型；性能指标；设计方法；优化策略；智能控制；案例研究；技术融合；创新设计；未来展望

参考资源链接：[现代控制系统（第十二版）谢红卫翻译习题解答指南](https://wenku.csdn.net/doc/3x2ahpqrky?spm=1055.2635.3001.10343)
# 1. 控制系统设计优化概述

## 引言
在现代工业和信息技术领域中，控制系统的设计和优化是保障系统稳定运行、提高效率的关键技术。本章节旨在概述控制系统设计优化的重要性，为后续章节中更深层次的理论分析、系统性能提升策略和实际案例应用打下基础。

## 控制系统设计优化的目的
控制系统设计优化的主要目的在于通过改进控制策略和算法，使系统达到或超过预定的技术指标，如稳定性、精度、快速响应和鲁棒性等。同时，优化工作也关注资源的合理配置，以实现能效比的最佳平衡。

## 控制系统设计优化的基本流程
优化流程通常包括系统分析、设计、模拟、测试及反馈调整等环节。首先，需建立系统的数学模型，并通过分析确定系统的关键性能指标。然后，根据性能要求设计和调整控制器参数，最后通过仿真或实际运行验证优化效果，并根据反馈进行进一步的调整优化。

以上是第一章的基本内容，为读者简要介绍了控制系统设计优化的目标、目的及基本流程，并为后续章节的具体分析和讨论奠定基础。

# 2. 控制系统基础理论与分析

控制系统是现代工业、航空、机器人技术及许多其他工程领域不可或缺的部分。它们确保了动态系统的性能满足设计要求。本章将深入探讨控制系统的基础理论，包括系统的数学模型、性能指标，以及控制系统设计的基本方法。

## 2.1 控制系统的数学模型

建立精确的数学模型是控制系统设计的第一步。数学模型通过使用数学方程来描述系统的动态行为，是分析和设计控制器的基础。

### 2.1.1 微分方程模型及其求解

微分方程模型是描述动态系统最常见的方式之一。它们能够捕捉到系统随时间变化的行为，并以此预测未来状态。

#### 例子：简单的二阶系统

假设有一个二阶系统的微分方程如下：

\[ m\ddot{x} + b\dot{x} + kx = f(t) \]

其中 \( m \) 是质量，\( b \) 是阻尼系数，\( k \) 是弹簧刚度，\( f(t) \) 是施加的外力，\( x \) 是位移。

为了解这个微分方程，我们可以使用拉普拉斯变换将其转换为代数方程。

from sympy import symbols, Eq, dsolve, Derivative, laplace_transform, Function
from sympy.abc import t, s

# 定义符号
m, b, k = symbols('m b k')
x = Function('x')(t)

# 定义微分方程
diffeq = Eq(m*Derivative(x, t, t) + b*Derivative(x, t) + k*x, f(t))

# 拉普拉斯变换
laplace_diffeq = laplace_transform(diffeq, t, s)

通过使用拉普拉斯变换，我们可以将微分方程转换为 \(s\) 的代数方程，并求解 \(X(s)\)，进而通过逆变换得到 \(x(t)\)。

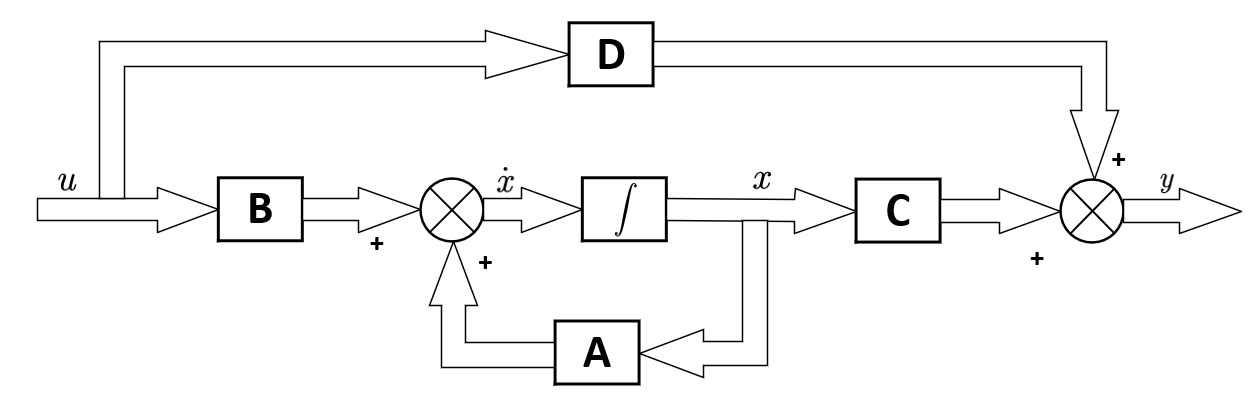
### 2.1.2 状态空间模型的建立和特性

状态空间模型提供了一种统一的方式来描述线性和非线性系统，特别是多变量系统。状态空间模型用状态方程和输出方程来表达系统的动态行为：

\[
\begin{align}
\dot{x}(t) &= Ax(t) + Bu(t) \\
y(t) &= Cx(t) + Du(t)
\end{align}
\]

其中，\(x(t)\) 是状态向量，\(u(t)\) 是输入向量，\(y(t)\) 是输出向量，\(A\)、\(B\)、\(C\) 和 \(D\) 是系统的矩阵。

#### 表格：状态空间模型参数说明

| 符号 | 描述 | 例子 |
| --- | --- | --- |
| \(x(t)\) | 状态向量 | 位置和速度 |
| \(u(t)\) | 输入向量 | 外力或控制信号 |
| \(y(t)\) | 输出向量 | 测量的位置或速度 |
| \(A\) | 状态矩阵 | 影响系统状态的动态特性 |
| \(B\) | 输入矩阵 | 将输入映射到系统状态 |
| \(C\) | 输出矩阵 | 决定状态如何影响输出 |
| \(D\) | 直接传递矩阵 | 输入直接传递到输出的系数 |

建立状态空间模型后，可以使用线性代数和控制理论中的方法进行分析和设计。

## 2.2 系统性能指标

性能指标是衡量控制系统是否达到期望性能的标准。它们包括稳定性、准确度、快速性以及系统响应的超调量。

### 2.2.1 稳定性分析

稳定性是控制系统最基本的要求。一个稳定的系统，在受到扰动后，其状态随时间趋向于平衡。

#### 流程图：系统稳定性分析

graph TD
    A[开始] --> B[定义系统方程]
    B --> C[求解系统特征方程]
    C --> D[检查特征根位置]
    D --> E{特征根是否都在左半平面}
    E -- 是 --> F[系统稳定]
    E -- 否 --> G[系统不稳定]
    F --> H[输出稳定性结果]
    G --> I[输出稳定性结果]

### 2.2.2 精度、快速性和超调量

- **精度**：系统响应与期望输出之间的接近程度。
- **快速性**：系统达到稳态的时间。
- **超调量**：系统响应超过稳态值的最大量。

这些性能指标是评估系统设计是否成功的重要依据。

## 2.3 系统设计的基本方法

设计一个有效的控制系统需要对系统行为有深入的理解。常见的控制方法包括PID控制和鲁棒控制策略。

### 2.3.1 PID控制原理与设计

PID（比例-积分-微分）控制器是最常用的控制策略之一。PID控制器由三个参数决定：比例（P）、积分（I）和微分（D）。PID控制器的目的是通过调整这三个参数来减少误差。

#### 代码块：PID控制器实现

class PIDController:
    def __init__(self, kp, ki, kd):
        self.kp = kp  # 比例增益
        self.ki = ki  # 积分增益
        self.kd = kd  # 微分增益
        self.previous_error = 0
        self.integral = 0

    def update(self, error, dt):
        self.integral += error * dt
        derivative = (error - self.previous_error) / dt
        output = self.kp*error + self.ki*self.integral + self.kd*derivative
        self.previous_error = error
        return output

# 参数说明：
# kp - 比例增益
# ki - 积分增益
# kd - 微分增益
# error - 当前误差
# dt - 时间间隔

### 2.3.2 鲁棒控制策略简析

鲁棒控制策略旨在设计出能够抵抗模型不确定性和外部扰动的控制系统。鲁棒控制通常依赖于系统的频域特性分析，使用H∞理论等方法设计控制器。

#### 例子：使用鲁棒控制理论设计控制器

在设计鲁棒控制系统时，首先需要确定系统的性能规格，比如频域中的增益和相位边界。然后使用优化技术来设计满足这些规格的控制器。

# 鲁棒控制理论相关代码通常较为复杂，可能涉及到优化算法，这里仅示意性展示
from scipy.optimize import minimize

# 性能规格示例
performance_specifications = {
    'gain_margin': 6,  # 增益边界
    'phase_margin': 45  # 相位边界
}

# 设计函数，用于优化控制器参数
def design_function(controller_params):
    # 这里省略了设计控制器参数的具体计算细节
    # 返回性能是否满足规格
    return is_performance_satisfied(controller_params, performance_specifications)

# 使用优化方法来调整控制器参数，直到性能满足规格
result = minimize(design_function, controller_params_initial_guess)

# 输出优化后的控制器参数
print(result.x)

在本章节中，我们介绍了控制系统的基础理论和分析方法。这些是控制系统设计和优化的关键组成部分。接下来的章节将继续深入探讨控制系统设计的习题解析以及如何通过优化策略进一步提高控制系统的性能。

# 3. 控制系统习题解析

## 3.1 典型控制问题的建模过程
在控制系统的研究与应用中，模型的建立是解决控制问题的基础。通过对控制系统进行建模，我们能够理解和分析系统的行为特性，进而提出有效的控制策略。

### 3.1.1 系统动态响应的分析
动态响应分析是指研究系统对输入信号的反应随时间变化的过程。在控制系统中，常见的输入信号包括阶跃信号、脉冲信号、正弦信号等。对于线性时不变系统（LTI系统），我们可以利用拉普拉斯变换来分析其动态响应。

以阶跃输入为例，系统的输出响应可以分为瞬态响应和稳态响应两部分。瞬态响应反映系统由初始状态过渡到稳态的过程，而稳态响应则表示系统在长时间运行后达到的平衡状态。

Y(s) = G(s) \cdot R(s)

上式中，`Y(s)` 是输出响应的拉普拉斯变换，`G(s)` 是系统的传递函数，而 `R(s)` 是输入信号的拉普拉斯变换。

### 3.1.2 参数识别与模型