揭秘遗传算法入门秘籍：轻松掌握进化之道

# 1. 遗传算法简介**

遗传算法（GA）是一种启发式搜索算法，它模拟了自然界中生物进化的过程来求解优化问题。GA通过迭代的方式，不断地选择、交叉和变异种群中的个体，以产生适应度更高的后代。

GA的灵感来自达尔文的进化论，它认为自然选择是生物进化的主要驱动力。在GA中，每个个体都代表一个潜在的解决方案，而适应度函数则衡量每个个体的优劣。适应度越高的个体更有可能被选择进行交叉和变异，从而产生更优的后代。

# 2.1 遗传算法的基本原理

### 2.1.1 自然选择与遗传

遗传算法（GA）是一种受自然进化过程启发的优化算法。它模拟了生物体如何通过自然选择和遗传变异适应环境。在自然界中，适应度高的个体更有可能生存和繁殖，从而将它们的基因传递给下一代。

在 GA 中，个体被编码为染色体，代表可能的解决方案。染色体的适应度由适应度函数决定，该函数衡量个体对特定问题的适用性。适应度高的个体更有可能被选择进行繁殖，从而产生具有更高适应度的后代。

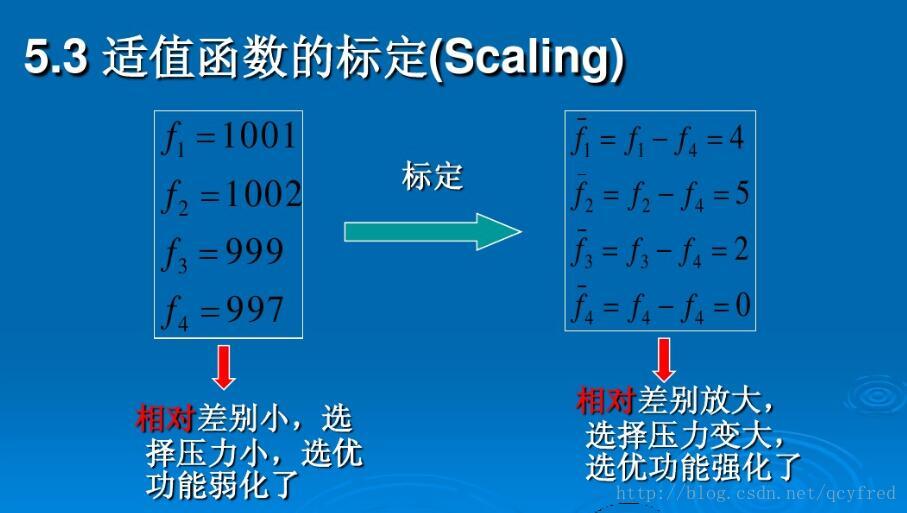
### 2.1.2 适应度函数

适应度函数是 GA 中的关键组件，它定义了每个个体的适应度。适应度函数可以是任何衡量个体对问题适用性的函数。对于不同的问题，适应度函数会不同。

例如，对于旅行商问题，适应度函数可以是旅行总距离的倒数。适应度高的个体表示旅行距离较短，更有可能被选择进行繁殖。

def fitness_function(chromosome):
  """计算旅行商问题的适应度函数。

  参数：
    chromosome: 表示旅行路线的染色体。

  返回：
    旅行总距离的倒数。
  """

  distance = calculate_total_distance(chromosome)
  return 1 / distance

适应度函数的设计对于 GA 的成功至关重要。它应该能够区分不同个体的适应度，并引导 GA 朝着更好的解决方案前进。

# 3. 遗传算法实践应用

### 3.1 遗传算法求解优化问题

遗传算法在优化问题求解中有着广泛的应用，可用于解决旅行商问题、函数优化等经典问题。

#### 3.1.1 旅行商问题

**问题描述：**
给定一组城市和城市之间的距离，求解一条最短的路径，使得每个城市都恰好被访问一次，最后回到出发城市。

**遗传算法求解步骤：**

1. **编码：**将城市顺序表示为染色体，每个基因代表一个城市。
2. **初始化：**随机生成一组染色体作为初始种群。
3. **适应度计算：**计算每个染色体的适应度，即路径长度的倒数。
4. **选择：**根据适应度对染色体进行选择，适应度高的染色体更有可能被选中。
5. **交叉：**将两个染色体进行交叉，生成新的染色体。
6. **变异：**对染色体进行变异，以引入多样性。
7. **重复步骤 3-6：**直到满足终止条件（如达到最大迭代次数或找到足够好的解）。

#### 3.1.2 函数优化

**问题描述：**
给定一个函数，求解函数的极值（最大值或最小值）。

**遗传算法求解步骤：**

1. **编码：**将函数参数表示为染色体，每个基因代表一个参数。
2. **初始化：**随机生成一组染色体作为初始种群。
3. **适应度计算：**计算每个染色体的适应度，即函数值。
4. **选择：**根据适应度对染色体进行选择，适应度高的染色体更有可能被选中。
5. **交叉：**将两个染色体进行交叉，生成新的染色体。
6. **变异：**对染色体进行变异，以引入多样性。
7. **重复步骤 3-6：**直到满足终止条件（如达到最大迭代次数或找到足够好的解）。

### 3.2 遗传算法在机器学习中的应用

遗传算法在机器学习中也得到了广泛应用，可用于解决分类问题、聚类问题等。

#### 3.2.1 分类问题

**问题描述：**
给定一组带标签的数据，训练一个模型来预测新数据的标签。

**遗传算法求解步骤：**

1. **编码：**将分类器的参数表示为染色体，每个基因代表一个参数。
2. **初始化：**随机生成一组染色体作为初始种群。
3. **适应度计算：**计算每个染色体的适应度，即分类器的准确率。
4. **选择：**根据适应度对染色体进行选择，适应度高的染色体更有可能被选中。
5. **交叉：**将两个染色体进行交叉，生成新的染色体。
6. **变异：**对染色体进行变异，以引入多样性。
7. **重复步骤 3-6：**直到满足终止条件（如达到最大迭代次数或找到足够好的解）。

#### 3.2.2 聚类问题

**问题描述：**
给定一组数据，将数据聚类成不同的组，使得同一组中的数据相似，不同组中的数据相异。

**遗传算法求解步骤：**

1. **编码：**将聚类器的参数表示为染色体，每个基因代表一个参数。
2. **初始化：**随机生成一组染色体作为初始种群。
3. **适应度计算：**计算每个染色体的适应度，即聚类器的聚类质量。
4. **选择：**根据适应度对染色体进行选择，适应度高的染色体更有可能被选中。
5. **交叉：**将两个染色体进行交叉，生成新的染色体。
6. **变异：**对染色体进行变异，以引入多样性。
7. **重复步骤 3-6：**直到满足终止条件（如达到最大迭代次数或找到足够好的解）。

# 4. 遗传算法进阶技术**

遗传算法是一种强大的优化算法，它通过模拟自然进化过程来解决复杂问题。在本章中，我们将探讨遗传算法的两个关键进阶技术：变异和交叉操作。这些操作对于保持种群多样性至关重要，从而提高算法的搜索效率和鲁棒性。

## 4.1 遗传算法的变异操作

变异操作通过随机改变个体的基因来引入种群多样性。这有助于防止算法陷入局部最优解，并探索新的解空间区域。有几种不同的变异操作，最常见的是：

### 4.1.1 单点变异

单点变异操作随机选择个体的单个基因，并将其值更改为预定义的范围内的另一个值。例如，对于二进制编码的个体，我们可以将基因从 0 更改为 1，反之亦然。

import random

def single_point_mutation(individual):
    """
    对个体执行单点变异操作。

    参数：
        individual: 要变异的个体。

    返回：
        变异后的个体。
    """

    # 随机选择一个基因位置
    gene_index = random.randint(0, len(individual) - 1)

    # 更改基因值
    individual[gene_index] = 1 - individual[gene_index]

    return individual

### 4.1.2 多点变异

多点变异操作类似于单点变异，但它同时更改多个基因的值。这可以增加多样性并加速收敛，但它也可能破坏个体的良好基因。

import random

def multi_point_mutation(individual, num_mutations):
    """
    对个体执行多点变异操作。

    参数：
        individual: 要变异的个体。
        num_mutations: 要变异的基因数量。

    返回：
        变异后的个体。
    """

    # 随机选择变异基因位置
    gene_indices = random.sample(range(len(individual)), num_mutations)

    # 更改基因值
    for gene_index in gene_indices:
        individual[gene_index] = 1 - individual[gene_index]

    return individual

## 4.2 遗传算法的交叉操作

交叉操作通过交换个体之间的基因来创建新的个体。这有助于结合不同个体的优势，并产生具有更高适应度的后代。有几种不同的交叉操作，最常见的是：

### 4.2.1 单点交叉

单点交叉操作随机选择一个交叉点，并将第一个个体的基因与交叉点后的第二个个体的基因交换。

import random

def single_point_crossover(parent1, parent2):
    """
    对两个父代个体执行单点交叉操作。

    参数：
        parent1: 第一个父代个体。
        parent2: 第二个父代个体。

    返回：
        两个交叉后的子代个体。
    """

    # 随机选择交叉点
    crossover_point = random.randint(0, len(parent1) - 1)

    # 交换基因
    child1 = parent1[:crossover_point] + parent2[crossover_point:]
    child2 = parent2[:crossover_point] + parent1[crossover_point:]

    return child1, child2

### 4.2.2 多点交叉

多点交叉操作类似于单点交叉，但它在多个点上交换基因。这可以增加多样性并加速收敛，但它也可能破坏个体的良好基因。

import random

def multi_point_crossover(parent1, parent2, num_crossovers):
    """
    对两个父代个体执行多点交叉操作。

    参数：
        parent1: 第一个父代个体。
        parent2: 第二个父代个体。
        num_crossovers: 交叉点的数量。

    返回：
        两个交叉后的子代个体。
    """

    # 随机选择交叉点
    crossover_points = random.sample(range(len(parent1)), num_crossovers)

    # 交换基因
    child1 = []
    child2 = []
    for i in range(len(parent1)):
        if i in crossover_points:
            child1.append(parent2[i])
            child2.append(parent1[i])
        else:
            child1.append(parent1[i])
            child2.append(parent2[i])

    return child1, child2

# 5.1 遗传算法在图像处理中的应用

### 5.1.1 图像增强

遗传算法在图像增强中可以用于优化图像的对比度、亮度和锐度。通过调整图像中像素的灰度值，遗传算法可以增强图像的细节和可视性。

**代码块：**

import numpy as np
import cv2

def image_enhancement(image, population_size, num_generations):
    # 初始化种群
    population = np.random.randint(0, 256, size=(population_size, image.shape[0], image.shape[1]))

    # 适应度函数（最大化图像对比度）
    def fitness_function(individual):
        contrast = cv2.Laplacian(individual, cv2.CV_64F).var()
        return contrast

    # 遗传算法主循环
    for generation in range(num_generations):
        # 计算适应度
        fitness = np.apply_along_axis(fitness_function, 1, population)

        # 选择
        parents = np.random.choice(population, population_size, replace=True, p=fitness / np.sum(fitness))

        # 交叉
        children = np.empty_like(population)
        for i in range(population_size):
            parent1, parent2 = parents[i % len(parents)], parents[(i + 1) % len(parents)]
            crossover_point = np.random.randint(0, image.shape[0])
            children[i] = np.concatenate((parent1[:crossover_point], parent2[crossover_point:]))

        # 变异
        for i in range(population_size):
            mutation_point = np.random.randint(0, image.shape[0])
            children[i][mutation_point] = np.random.randint(0, 256)

        # 更新种群
        population = children

    # 返回增强后的图像
    return population[np.argmax(fitness)]

**逻辑分析：**

* 初始化种群，其中每个个体表示一张图像。
* 定义适应度函数以最大化图像对比度。
* 迭代执行遗传算法主循环：
* 计算个体的适应度。
* 根据适应度选择父代。
* 通过单点交叉生成子代。
* 通过单点变异引入多样性。
* 更新种群。
* 返回适应度最高的个体，即增强后的图像。

### 5.1.2 图像分割

遗传算法还可以用于图像分割，即将图像分割成具有不同特征的区域。通过优化分割区域的形状和位置，遗传算法可以提高分割的准确性和鲁棒性。

**代码块：**

import numpy as np
import cv2

def image_segmentation(image, population_size, num_generations):
    # 初始化种群
    population = np.random.randint(0, 256, size=(population_size, image.shape[0], image.shape[1]))

    # 适应度函数（最大化分割区域的同质性）
    def fitness_function(individual):
        segmented_image = cv2.watershed(image, individual)
        homogeneity = np.sum(np.var(segmented_image, axis=0))
        return homogeneity

    # 遗传算法主循环
    for generation in range(num_generations):
        # 计算适应度
        fitness = np.apply_along_axis(fitness_function, 1, population)

        # 选择
        parents = np.random.choice(population, population_size, replace=True, p=fitness / np.sum(fitness))

        # 交叉
        children = np.empty_like(population)
        for i in range(population_size):
            parent1, parent2 = parents[i % len(parents)], parents[(i + 1) % len(parents)]
            crossover_point = np.random.randint(0, image.shape[0])
            children[i] = np.concatenate((parent1[:crossover_point], parent2[crossover_point:]))

        # 变异
        for i in range(population_size):
            mutation_point = np.random.randint(0, image.shape[0])
            children[i][mutation_point] = np.random.randint(0, 256)

        # 更新种群
        population = children

    # 返回分割后的图像
    return population[np.argmax(fitness)]

**逻辑分析：**

* 初始化种群，其中每个个体表示一张图像分割掩码。
* 定义适应度函数以最大化分割区域的同质性。
* 迭代执行遗传算法主循环：
* 计算个体的适应度。
* 根据适应度选择父代。
* 通过单点交叉生成子代。
* 通过单点变异引入多样性。
* 更新种群。
* 返回适应度最高的个体，即分割后的图像。

# 6. 遗传算法的未来发展**

遗传算法作为一种强大的优化算法，在解决复杂问题方面展现出巨大的潜力。随着技术的发展，遗传算法的未来发展方向主要集中在以下两个方面：

**6.1 遗传算法与深度学习的结合**

深度学习是一种机器学习技术，它利用多层神经网络来学习复杂数据的特征。遗传算法可以与深度学习相结合，优化神经网络的结构和超参数，从而提升深度学习模型的性能。例如，遗传算法可以用来优化神经网络的层数、节点数、激活函数和学习率等参数。

**6.2 遗传算法在人工智能领域的应用**

遗传算法在人工智能领域有着广泛的应用前景。它可以用来解决人工智能中的各种问题，例如：

* **自然语言处理：**优化文本分类、机器翻译和问答系统的性能。
* **计算机视觉：**优化图像识别、目标检测和图像分割算法。
* **强化学习：**优化强化学习算法的策略，提高其在复杂环境中的决策能力。
* **无人驾驶：**优化无人驾驶汽车的路径规划和决策制定算法。

**示例代码：**

以下代码展示了如何使用遗传算法优化神经网络的结构：

import numpy as np
import tensorflow as tf

# 定义神经网络结构
class NeuralNetwork:
    def __init__(self, layers):
        self.layers = layers

    def forward(self, x):
        # 正向传播
        for layer in self.layers:
            x = layer(x)
        return x

# 定义遗传算法
class GeneticAlgorithm:
    def __init__(self, population_size, mutation_rate, crossover_rate):
        self.population_size = population_size
        self.mutation_rate = mutation_rate
        self.crossover_rate = crossover_rate

    def evaluate(self, population):
        # 评估种群中的个体
        fitness = []
        for individual in population:
            fitness.append(individual.fitness)
        return fitness

    def select(self, population, fitness):
        # 选择种群中的个体
        selected_population = []
        for i in range(self.population_size):
            # 随机选择个体
            index = np.random.choice(len(population), p=fitness / np.sum(fitness))
            selected_population.append(population[index])
        return selected_population

    def crossover(self, population):
        # 交叉操作
        new_population = []
        for i in range(0, len(population), 2):
            # 随机选择两个个体
            parent1 = population[i]
            parent2 = population[i+1]
            # 交叉操作
            if np.random.rand() < self.crossover_rate:
                crossover_point = np.random.randint(1, len(parent1.layers))
                new_individual = NeuralNetwork(parent1.layers[:crossover_point] + parent2.layers[crossover_point:])
            else:
                new_individual = parent1
            new_population.append(new_individual)
        return new_population

    def mutate(self, population):
        # 变异操作
        for individual in population:
            # 随机选择一个层
            layer_index = np.random.randint(len(individual.layers))
            # 随机修改层的参数
            if np.random.rand() < self.mutation_rate:
                individual.layers[layer_index] = tf.keras.layers.Dense(np.random.randint(1, 100), activation='relu')
        return population

    def run(self, population):
        # 运行遗传算法
        for generation in range(100):
            # 评估种群
            fitness = self.evaluate(population)
            # 选择种群
            selected_population = self.select(population, fitness)
            # 交叉操作
            new_population = self.crossover(selected_population)
            # 变异操作
            new_population = self.mutate(new_population)
            # 更新种群
            population = new_population
        # 返回最优个体
        return population[np.argmax(fitness)]