遗传算法优化大法：从理论到实践，解决难题无往不利

# 1. 遗传算法的理论基础**

遗传算法是一种受生物进化启发的优化算法。它模拟了自然选择的过程，通过迭代地选择、交叉和变异个体来优化目标函数。

遗传算法的基本原理包括：

* **编码和解码：**将问题解决方案编码为二进制字符串或其他表示形式。
* **适应度函数：**评估每个个体的适应度，即其对目标函数的适应程度。
* **选择：**根据适应度选择个体进行繁殖，适应度高的个体更有可能被选中。
* **交叉：**将两个个体的基因片段交换，产生新的个体。
* **变异：**随机改变个体的基因，引入多样性并防止算法陷入局部最优解。

# 2. 遗传算法的编程实现

### 2.1 遗传算法的基本流程

遗传算法的基本流程包括以下步骤：

**2.1.1 编码和解码**

编码是将问题的解表示为遗传算法中的染色体。解码是将染色体映射回问题的解空间。常见的编码方法有二进制编码、实数编码和树形编码。

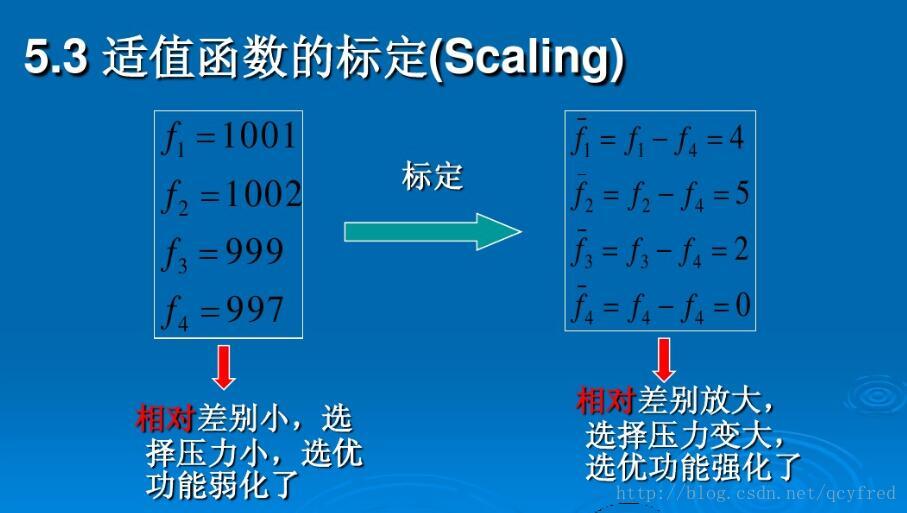
**2.1.2 适应度函数**

适应度函数衡量个体的优劣程度。它将个体的染色体映射到一个实数，表示个体的适应度。适应度高的个体更有可能被选中进行繁殖。

**2.1.3 选择、交叉和变异**

* **选择：**根据适应度对个体进行选择，适应度高的个体更有可能被选中进行繁殖。常用的选择方法有轮盘赌选择、锦标赛选择和精英选择。
* **交叉：**交叉是将两个父代个体的染色体片段交换，产生新的子代个体。常用的交叉方法有单点交叉、两点交叉和均匀交叉。
* **变异：**变异是随机改变个体染色体的某个基因，以引入多样性。常用的变异方法有位翻转变异、交换变异和插入变异。

### 2.2 遗传算法的优化策略

#### 2.2.1 参数优化

遗传算法的参数包括种群规模、世代数、选择概率、交叉概率和变异概率。这些参数需要根据具体问题进行优化。

#### 2.2.2 种群规模和世代数

种群规模和世代数影响遗传算法的收敛速度和搜索能力。一般来说，较大的种群规模和世代数可以提高算法的收敛速度，但也会增加计算成本。

#### 2.2.3 多目标优化

遗传算法可以用于解决多目标优化问题，即同时优化多个目标函数。常用的多目标优化方法有NSGA-II算法和SPEA2算法。

# 3. 遗传算法的实践应用

遗传算法在解决实际问题中有着广泛的应用，涵盖了连续优化、组合优化和约束优化等多种类型的问题。本章节将介绍遗传算法在这些不同类型问题中的具体应用，并通过示例展示其解决问题的步骤和效果。

### 3.1 连续优化问题

#### 3.1.1 函数优化

函数优化问题是指寻找一个函数的最小值或最大值。遗传算法可以有效地解决此类问题，其基本思路是将函数的输入变量编码成染色体，并通过适应度函数评估染色体的优劣。

import numpy as np
import random

# 目标函数
def objective_function(x):
    return x**2 + 10*np.sin(x)

# 遗传算法参数
population_size = 100
generations = 100
crossover_rate = 0.8
mutation_rate = 0.2

# 初始化种群
population = [random.uniform(-10, 10) for _ in range(population_size)]

# 遗传算法主循环
for generation in range(generations):
    # 计算适应度
    fitness = [objective_function(x) for x in population]

    # 选择
    parents = selection(population, fitness)

    # 交叉
    offspring = crossover(parents, crossover_rate)

    # 变异
    offspring = mutation(offspring, mutation_rate)

    # 更新种群
    population = offspring

# 输出最优解
best_solution = min(population, key=objective_function)
print("最优解：", best_solution)

**代码逻辑分析：**

* `objective_function()`函数定义了目标函数。
* `population`数组存储了种群中的个体，每个个体是一个实数。
* 遗传算法的主循环运行指定代数。
* `selection()`函数根据适应度选择父母个体。
* `crossover()`函数以指定概率对父母个体进行交叉操作。
* `mutation()`函数以指定概率对后代个体进行变异操作。
* 最后，输出适应度最高的个体作为最优解。

#### 3.1.2 参数估计

参数估计问题是指从观测数据中估计模型参数。遗传算法可以利用观测数据来搜索最优的参数值，从而提高模型的预测精度。

import numpy as np
import random

# 目标函数（模型预测误差）
def objective_function(params, data):
    # 根据参数预测模型输出
    predictions = model(data, params)

    # 计算预测误差
    error = np.mean((predictions - data)**2)

    return error

# 遗传算法参数
population_size = 100
generations = 100
crossover_rate = 0.8
mutation_rate = 0.2

# 初始化种群
population = [random.uniform(-10, 10) for _ in range(population_size)]

# 遗传算法主循环
for generation in range(generations):
    # 计算适应度
    fitness = [objective_function(x, data) for x in population]

    # 选择
    parents = selection(population, fitness)

    # 交叉
    offspring = crossover(parents, crossover_rate)

    # 变异
    offspring = mutation(offspring, mutation_rate)

    # 更新种群
    population = offspring

# 输出最优解
best_params = min(population, key=objective_function)
print("最优参数：", best_params)

**代码逻辑分析：**

* `objective_function()`函数计算模型预测误差。
* `population`数组存储了种群中的个体，每个个体是一个参数向量。
* 遗传算法的主循环运行指定代数。
* `selection()`函数根据适应度选择父母个体。
* `crossover()`函数以指定概率对父母个体进行交叉操作。
* `mutation()`函数以指定概率对后代个体进行变异操作。
* 最后，输出适应度最高的个体作为最优参数值。

### 3.2 组合优化问题

#### 3.2.1 旅行商问题

旅行商问题是指给定一组城市和城市之间的距离，寻找一条最短的路径，访问所有城市并返回起点。遗传算法可以将城市编码成染色体，并通过适应度函数评估路径的长度。

import numpy as np
import random

# 城市坐标
cities = [(0, 0), (10, 0), (0, 10), (10, 10)]

# 距离矩阵
distances = np.zeros((len(cities), len(cities)))
for i in range(len(cities)):
    for j in range(len(cities)):
        distances[i][j] = np.linalg.norm(np.array(cities[i]) - np.array(cities[j]))

# 遗传算法参数
population_size = 100
generations = 100
crossover_rate = 0.8
mutation_rate = 0.2

# 初始化种群
population = [random.sample(range(len(cities)), len(cities)) for _ in range(population_size)]

# 遗传算法主循环
for generation in range(generations):
    # 计算适应度
    fitness = [1 / total_distance(x, distances) for x in population]

    # 选择
    parents = selection(population, fitness)

    # 交叉
    offspring = crossover(parents, crossover_rate)

    # 变异
    offspring = mutation(offspring, mutation_rate)

    # 更新种群
    population = offspring

# 输出最优解
best_tour = min(population, key=lambda x: total_distance(x, distances))
print("最优路径：", best_tour)

**代码逻辑分析：**

* `distances`矩阵存储了城市之间的距离。
* `population`数组存储了种群中的个体，每个个体是一个城市序列。
* 遗传算法的主循环运行指定代数。
* `selection()`函数根据适应度选择父母个体。
* `crossover()`函数以指定概率对父母个体进行交叉操作。
* `mutation()`函数以指定概率对后代个体进行变异操作。
* `total_distance()`函数计算路径的总距离。
* 最后，输出适应度最高的个体作为最优路径。

#### 3.2.2 背包问题

背包问题是指给定一组物品，每件物品都有重量和价值，以及一个背包容量，寻找一个物品集合，在不超过背包容量的情况下，使总价值最大。遗传算法可以将物品编码成染色体，并通过适应度函数评估背包的总价值。

import numpy as np
import random

# 物品信息
items = [
    {"weight": 2, "value": 3},
    {"weight": 3, "value": 4},
    {"weight": 4, "value": 5},
    {"weight": 5, "value": 6},
]

# 背包容量
capacity = 10

# 遗传算法参数
population_size = 100
generations = 100
crossover_rate = 0.8
mutation_rate = 0.2

# 初始化种群
population = [random.choices([0, 1], k=len(items)) for _ in range(population_size)]

# 遗传算法主循环
for generation in range(generations):
    # 计算适应度
    fitness = [total_value(x, items) for x in population]

    # 选择
    parents = selection(population, fitness)

    # 交叉
    offspring = crossover(parents, crossover_rate)

    # 变异
    offspring = mutation(offspring, mutation_rate)

    # 更新种群
    population = offspring

# 输出最优解
best_items = min(population, key=lambda x: total_value(x, items))
print("最优物品集合：", best_items)

**代码逻辑分析：**

* `items`列表存储了物品信息，包括重量和价值。
* `population`数组存储了种群中的个体，每个个体是一个二进制序列，表示是否选择相应的物品。
* 遗传算法的主循环运行指定代数。
* `selection()`函数根据适应度选择父母个体。
* `crossover()`函数以指定概率对父母个体进行交叉操作。
* `mutation()`函数以指定概率对后代个体进行变异操作。
* `total_value()`函数计算背包的总价值。
* 最后，输出适应度最高的个体作为最优物品集合。

# 4. 遗传算法的扩展和应用

### 4.1 多目标遗传算法

遗传算法可以扩展到解决具有多个目标的优化问题，称为多目标遗传算法（MOEA）。MOEA 通过同时优化多个目标来找到一组非支配解，这些解在所有目标上都具有良好的性能。

**4.1.1 NSGA-II 算法**

NSGA-II（非支配排序遗传算法 II）是一种流行的 MOEA，它使用非支配排序和拥挤距离来选择和保留非支配解。NSGA-II 算法的步骤如下：

def nsga2(population, objectives, generations):
    """NSGA-II 算法

    Args:
        population (list): 种群
        objectives (list): 目标函数
        generations (int): 世代数

    Returns:
        list: 非支配解集合
    """

    # 初始化
    fronts = fast_non_dominated_sort(population, objectives)
    crowding_distances = calculate_crowding_distances(fronts)

    for _ in range(generations):
        # 选择
        parents = tournament_selection(population, crowding_distances)

        # 交叉和变异
        offspring = crossover_and_mutate(parents)

        # 评估
        evaluate(offspring, objectives)

        # 合并种群
        combined_population = population + offspring

        # 非支配排序
        fronts = fast_non_dominated_sort(combined_population, objectives)

        # 拥挤距离计算
        crowding_distances = calculate_crowding_distances(fronts)

        # 选择下一代
        population = select_next_generation(combined_population, fronts, crowding_distances)

    return population

**代码逻辑逐行解读：**

1. `fast_non_dominated_sort` 函数：根据非支配关系对种群进行排序，返回非支配解集合。
2. `calculate_crowding_distances` 函数：计算每个解的拥挤距离，拥挤距离大的解表示周围有较多其他解，拥挤距离小的解表示周围有较少其他解。
3. `tournament_selection` 函数：使用锦标赛选择方法选择父代。
4. `crossover_and_mutate` 函数：对父代进行交叉和变异操作，产生子代。
5. `evaluate` 函数：对子代进行评估，计算目标函数值。
6. `select_next_generation` 函数：根据非支配关系和拥挤距离选择下一代种群。

**4.1.2 SPEA2 算法**

SPEA2（实力估计进化算法 2）是一种另一种流行的 MOEA，它使用实力估计和归档机制来维护非支配解集合。SPEA2 算法的步骤如下：

def spea2(population, objectives, generations):
    """SPEA2 算法

    Args:
        population (list): 种群
        objectives (list): 目标函数
        generations (int): 世代数

    Returns:
        list: 非支配解集合
    """

    # 初始化
    archive = []
    for individual in population:
        if individual.is_non_dominated(population, objectives):
            archive.append(individual)

    for _ in range(generations):
        # 选择
        parents = tournament_selection(population)

        # 交叉和变异
        offspring = crossover_and_mutate(parents)

        # 评估
        evaluate(offspring, objectives)

        # 合并种群
        combined_population = population + offspring

        # 实力估计
        strengths = calculate_strengths(combined_population)

        # 归档
        archive = update_archive(archive, combined_population, strengths)

        # 选择下一代
        population = select_next_generation(combined_population, strengths)

    return archive

**代码逻辑逐行解读：**

1. `is_non_dominated` 方法：判断一个解是否为非支配解。
2. `calculate_strengths` 函数：计算每个解的优势解数量，即该解被多少个解支配。
3. `update_archive` 函数：根据实力估计和归档机制更新归档集合。
4. `select_next_generation` 函数：根据实力估计选择下一代种群。

# 5. 遗传算法在实际问题中的应用案例**

遗传算法在实际问题中有着广泛的应用，以下列举几个典型的应用案例：

**5.1 机器学习模型优化**

遗传算法可用于优化机器学习模型的参数，以提高模型的性能。

**5.1.1 神经网络调优**

神经网络是一种强大的机器学习模型，但其性能受超参数（如学习率、层数和神经元数）的影响很大。遗传算法可用于搜索这些超参数的最佳组合，从而优化神经网络的性能。

import numpy as np
import tensorflow as tf

# 定义神经网络模型
model = tf.keras.models.Sequential([
  tf.keras.layers.Dense(128, activation='relu', input_shape=(784,)),
  tf.keras.layers.Dense(10, activation='softmax')
])

# 定义遗传算法参数
population_size = 100
generations = 100

# 初始化遗传算法
ga = GeneticAlgorithm(population_size, generations)

# 定义适应度函数
def fitness_function(params):
  # 将参数应用于神经网络模型
  model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=params[0]),
                loss='sparse_categorical_crossentropy',
                metrics=['accuracy'])

  # 训练模型
  model.fit(X_train, y_train, epochs=10)

  # 返回模型的准确率
  return model.evaluate(X_test, y_test)[1]

# 运行遗传算法
best_params = ga.run(fitness_function)

# 使用最佳参数训练神经网络模型
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=best_params[0]),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])
model.fit(X_train, y_train, epochs=10)

**5.1.2 支持向量机参数优化**

支持向量机（SVM）是一种分类算法，其性能受核函数类型、惩罚参数和核函数参数等超参数的影响。遗传算法可用于优化这些超参数，从而提高 SVM 的分类精度。

import numpy as np
from sklearn.svm import SVC

# 定义 SVM 模型
model = SVC()

# 定义遗传算法参数
population_size = 100
generations = 100

# 初始化遗传算法
ga = GeneticAlgorithm(population_size, generations)

# 定义适应度函数
def fitness_function(params):
  # 将参数应用于 SVM 模型
  model.kernel = params[0]
  model.C = params[1]
  model.gamma = params[2]

  # 训练模型
  model.fit(X_train, y_train)

  # 返回模型的准确率
  return model.score(X_test, y_test)

# 运行遗传算法
best_params = ga.run(fitness_function)

# 使用最佳参数训练 SVM 模型
model.kernel = best_params[0]
model.C = best_params[1]
model.gamma = best_params[2]
model.fit(X_train, y_train)