【多变量数据处理指南】：因子分析从理论到实战的完整教程

目录
摘要
关键字
1. 多变量数据处理与因子分析概述

1.1 数据处理的重要性
1.2 因子分析的定义和用途
1.3 从简单到复杂：因子分析的演变

2. 因子分析理论基础

2.1 因子分析的概念和数学模型

2.1.1 因子分析的定义和应用场景
2.1.2 因子模型的构建与假设

2.2 因子分析的数学原理

2.2.1 相关矩阵和主成分分析
2.2.2 因子提取方法：主成分法和主轴因子法
2.2.3 因子旋转技术

2.3 因子分析的统计检验

2.3.1 KMO和Bartlett球形检验
2.3.2 因子载荷的显著性检验
2.3.3 因子得分的计算与解释

结语

3. 因子分析的软件实现

3.1 SPSS中进行因子分析的步骤与技巧

数据准备与初步处理
运行因子分析并解释结果

解锁专栏，查看完整目录
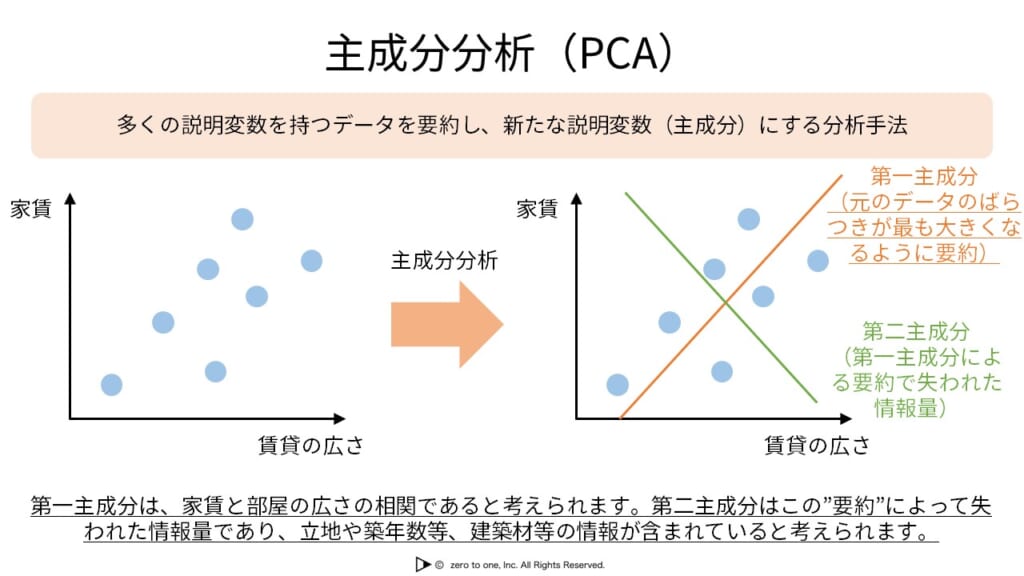
摘要
因子分析作为一种多变量数据处理技术，在社会科学、心理学、市场研究等领域有着广泛应用。本文首先概述了因子分析的概念、数学模型及应用场景，并详细探讨了其理论基础，包括因子模型构建、数学原理、统计检验以及因子旋转技术。接着，本文阐述了如何在SPSS、R语言和Python中实现因子分析，并提供了详细的步骤和技巧。此外，本文还介绍了高级主题，如多阶因子分析、与其它多变量分析方法的整合，以及行业应用案例。最后，本文讨论了在实践因子分析过程中可能遇到的挑战、解决方案、局限性以及未来发展趋势，特别是在新兴技术和大数据环境下的应用前景。
关键字
因子分析；多变量数据处理；数学模型；统计检验；软件实现；行业应用案例；未来趋势
参考资源链接：eviews中主成分分析和因子分析详解PPT学习教案.pptx
1. 多变量数据处理与因子分析概述
1.1 数据处理的重要性
在数据分析领域，数据处理是将原始数据转换为有用信息的关键步骤。特别是当涉及到多变量数据集时，变量之间可能存在着复杂的关系和模式。多变量数据处理技术允许我们挖掘这些深层次的关系，并将数据简化为可解释的形式。
1.2 因子分析的定义和用途
因子分析是一种统计方法，它通过发现数据中的潜在因子来解释变量间的共变性。这些潜在因子可以帮助我们理解数据背后的结构，减少数据维度，并在数据分析、变量选择和数据压缩中发挥重要作用。它的应用范围广泛，从市场研究到心理学，因子分析都是处理多变量数据的强大工具。
1.3 从简单到复杂：因子分析的演变
因子分析的历史可以追溯到20世纪初，但其理论和应用一直不断发展。最初，它是作为一种探索性技术出现的，现在它不仅适用于探索性研究，还可以用于验证性研究，成为结构方程模型的一个组成部分。这门技术的持续演进揭示了数据科学在处理复杂数据时的无限可能。
通过本章的介绍，我们已经搭建了因子分析的基本概念框架，并准备好深入探讨其理论基础和实际应用。接下来的章节将带您逐步深入了解因子分析的数学原理和在不同软件环境下的操作实践。
2. 因子分析理论基础
2.1 因子分析的概念和数学模型
2.1.1 因子分析的定义和应用场景
因子分析是一种统计技术，旨在研究多个变量间相关性的原因，并将这些变量归纳为数量较少的、不可观测的潜在变量，即因子。这些因子能够解释原始变量的相关性，并帮助研究者理解数据的基本结构。
因子分析在多个领域有广泛应用，包括心理学、市场营销、社会科学和质量管理等领域。例如，在心理测量学中，因子分析可以帮助研究者了解在大量问卷调查中各个问题背后的潜在结构；在市场研究中，它有助于揭示消费者态度和行为背后的潜在驱动因素。
2.1.2 因子模型的构建与假设
构建因子模型的基本假设是：(1) 变量间的相关性可以通过数量有限的潜在因子来解释；(2) 潜在因子与误差项相互独立；(3) 潜在因子之间也相互独立。
构建因子模型的第一步是确定相关矩阵，然后通过因子提取过程确定潜在因子的数量和结构。在实际操作中，研究者还需要根据数据的特性和研究目的来选择因子提取方法和因子旋转技术。
2.2 因子分析的数学原理
2.2.1 相关矩阵和主成分分析
因子分析常常从变量的相关矩阵开始。相关矩阵展示了变量间的线性相关程度。高相关性意味着潜在因子对这些变量具有较强的解释力。在相关矩阵的基础上，可以应用主成分分析（PCA）提取因子。PCA是一种降维技术，它通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，即主成分。
PCA的目标是提取出方差最大的主成分，每个主成分都是原始变量的加权和，权重由特征向量给出。提取的主成分累计方差贡献率是因子分析中选择因子数量的重要参考标准。
2.2.2 因子提取方法：主成分法和主轴因子法
在因子分析中，常用的提取方法有主成分法和主轴因子法。主成分法通过最大化提取的因子方差来提取因子，而主轴因子法则在提取因子时考虑了变量的共同方差。
主成分法假设一个因子的方差等于1，而主轴因子法则允许因子的方差自由估计。这两种方法在处理相关矩阵时有所不同，主成分法更侧重于解释数据的总体变异性，而主轴因子法则更侧重于解释变量间的共同变异性。
2.2.3 因子旋转技术
在因子提取后，通常需要进行因子旋转以获得更清晰的因子结构。因子旋转的目的是简化因子载荷矩阵，使每个因子只在少数变量上有较大的载荷，而与其他变量的载荷接近于零。
有两种主要的旋转技术：正交旋转和斜交旋转。正交旋转保持因子间的独立性，例如方差最大化（Varimax）旋转；斜交旋转则允许因子之间存在相关性，例如Oblimin旋转。选择合适的旋转技术对于解释因子模型至关重要。
2.3 因子分析的统计检验
2.3.1 KMO和Bartlett球形检验
在进行因子分析之前，需要检验数据是否适合做因子分析。KMO（Kaiser-Meyer-Olkin）检验用于测量变量间的偏相关性，值越接近1表示变量间的偏相关性越低，做因子分析的效果越好。Bartlett球形检验则用于检验变量间的相关矩阵是否为单位矩阵，即变量是否相互独立。若检验结果不拒绝原假设，则数据不适合做因子分析。
2.3.2 因子载荷的显著性检验
因子载荷指的是变量与因子之间的相关系数。因子载荷的显著性检验有助于判断某个变量是否与某个因子显著相关。通过检验，研究者可以确定哪些变量与因子相关性显著，从而对因子进行命名和解释。
2.3.3 因子得分的计算与解释
因子得分是每个观测在潜在因子上的值，它是原始变量的加权线性组合。因子得分可以用于进一步的分析，例如聚类分析或回归分析。因子得分的计算基于因子载荷和变量值，是一个解释性的过程，使得每个观测的因子得分可以代表其在潜在因子上的位置。
结语
因子分析是探索多变量数据内在结构的有力工具。理解因子分析的基本概念、数学模型、提取方法、旋转技术和统计检验，对于有效运用这一技术至关重要。本章节中，我们详细探讨了因子分析的理论基础和相关数学原理，为后续章节中实际应用因子分析提供了坚实的理论支持。接下来的章节将聚焦于因子分析的软件实现，展示如何通过不同的统计软件进行因子分析，将理论应用于实践。
3. 因子分析的软件实现
3.1 SPSS中进行因子分析的步骤与技巧
数据准备与初步处理
在使用SPSS进行因子分析之前，数据的准备和初步处理是非常关键的一步。首先需要对数据进行检查，确保数据的准确性和完整性。接下来，对数据进行清洗，包括识别并处理缺失值、异常值和数据标准化等步骤。SPSS中可以通过Data -> Select Cases进行数据筛选，使用Transform -> Compute Variable进行数据转换。
运行因子分析并解释结果
在SPSS中，因子分析的执行可以通过Analyze -> Dimension Reduction -> Factor...路径实现。在打开的对话框中，用户需要将研究中关注的变量选入`Var