【深度解读】：反向传播算法，神经网络学习背后的秘密

# 1. 神经网络基础知识

在本章中，我们将揭开神经网络的神秘面纱，了解其核心组件和基本工作原理。首先，我们将探讨神经网络的基本结构和类型，例如前馈神经网络和递归神经网络，这些构成了深度学习的基础。之后，我们将详细介绍神经元的工作机制，以及它们是如何通过加权输入和激活函数的非线性转换来产生输出的。我们还将对激活函数进行深入分析，了解它们在引入非线性以及控制神经网络输出方面的重要性。这些基础知识为理解后续章节中的反向传播算法和其优化技术打下坚实的基础。

## 1.1 神经网络的组成
神经网络由多个神经元组成，神经元之间相互连接。每个连接都带有权重，表示神经元间的信号强度。输入层接收外界数据，隐藏层负责处理信息，最后输出层给出结果。

## 1.2 前馈神经网络和递归神经网络
前馈神经网络的信息流动是单向的，从输入层到隐藏层再到输出层。而递归神经网络允许层与层之间的反馈连接，常用于处理序列数据，如语音和文本。

## 1.3 激活函数的作用
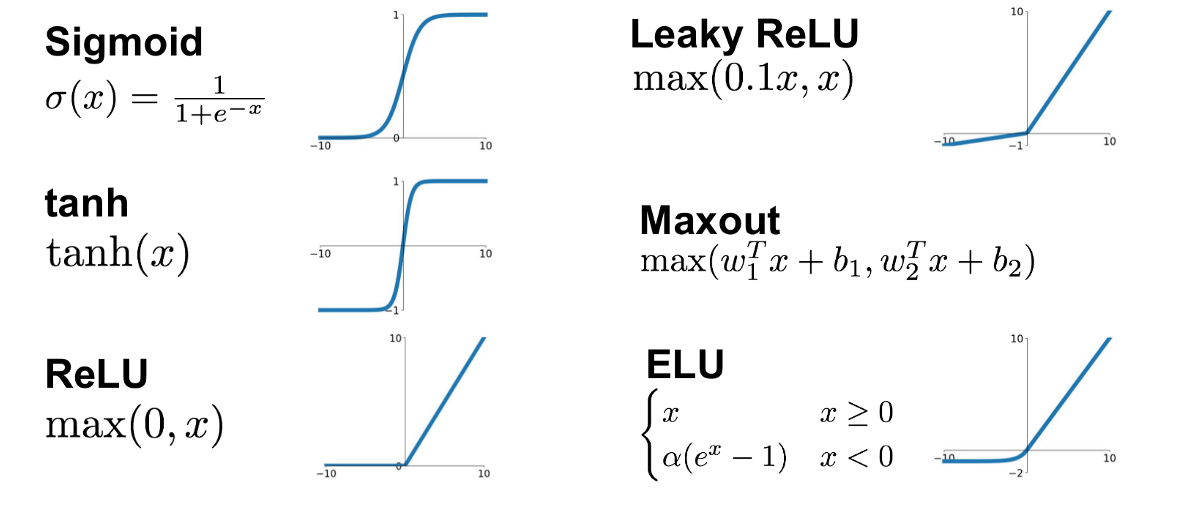
激活函数引入了非线性因素，使神经网络能够学习和执行复杂的任务。常见的激活函数包括Sigmoid、ReLU和Tanh等，每个都有其适用场景和优势。

# 2. 反向传播算法理论基础

### 2.1 神经网络的前向传播机制

#### 数据的流动和处理

在神经网络中，数据的流动遵循前向传播的机制。数据从输入层开始，逐层传递至输出层，每一层的神经元处理来自前一层的加权输入，并通过激活函数产生输出。这一过程可以视为连续的非线性变换。

考虑一个简单的全连接层，它的输入可以表示为矩阵 \(X\)，每一列代表一个样本，每一行代表一个特征。权重矩阵 \(W\) 存储了层与层之间连接的权重，而偏置向量 \(b\) 用于调整输出。前向传播的数学表达式可以写为：

\[
Z = XW + b
\]
\[
A = g(Z)
\]

其中，\(g\) 为激活函数，\(Z\) 为线性变换的结果，而 \(A\) 为激活后的输出。这个过程会重复执行，直到最后一个隐藏层，最终产生预测结果。

#### 激活函数的选择与作用

激活函数是神经网络中引入非线性的关键因素，它允许神经网络学习并执行复杂的任务。常见的激活函数包括 Sigmoid、ReLU、tanh 等。

以 ReLU 为例，它的数学表达式为：

\[
f(x) = max(0, x)
\]

在前向传播中，ReLU 函数通过抑制小于 0 的值来实现非线性。其作用包括：

- 提高模型非线性拟合能力。
- 缓解梯度消失问题，因为其导数为常数 \(1\)（对于正值）。
- 计算效率高，实现简单。

### 2.2 反向传播算法的原理

#### 损失函数与误差分析

反向传播算法的核心是基于梯度下降法的优化过程。首先需要定义一个损失函数 \(L\)，用于衡量模型预测与真实值之间的差异。对于分类问题，常用的损失函数是交叉熵损失：

\[
L(y, \hat{y}) = - \sum_{i} y_i \log(\hat{y}_i)
\]

在训练过程中，损失函数需要被最小化，这通常通过计算损失函数相对于权重的梯度来实现。梯度指向损失函数增长最快的方向，反方向即为损失函数减小最快的方向。

#### 链式法则在反向传播中的应用

为了计算损失函数相对于每个权重的梯度，反向传播使用链式法则计算所有节点的梯度。链式法则是微积分中一个用来求复合函数导数的方法。

假定一个从输入 \(X\) 到输出 \(O\) 的复合函数 \(O = f(g(h(X)))\)，则其导数可按链式法则分解为：

\[
\frac{\partial O}{\partial X} = \frac{\partial O}{\partial f} \cdot \frac{\partial f}{\partial g} \cdot \frac{\partial g}{\partial h} \cdot \frac{\partial h}{\partial X}
\]

在神经网络中，对于每个权重 \(W_{ij}\)，我们需要计算损失函数 \(L\) 相对于 \(W_{ij}\) 的偏导数：

\[
\frac{\partial L}{\partial W_{ij}} = \frac{\partial L}{\partial A_k} \cdot \frac{\partial A_k}{\partial Z_k} \cdot \frac{\partial Z_k}{\partial W_{ij}}
\]

其中 \(A_k\) 是第 \(k\) 层的激活值，\(Z_k\) 是该层的线性变换结果。

### 2.3 权重更新与梯度下降

#### 梯度下降的基本概念

梯度下降是一种用来优化损失函数的算法。其基本思想是将损失函数 \(L\) 看作一个地形图，模型参数（如权重 \(W\) 和偏置 \(b\)）作为在这个地形上的位置。梯度下降的目标是找到最低点，即最小化损失。

梯度下降的更新规则如下：

\[
W := W - \eta \frac{\partial L}{\partial W}
\]

\[
b := b - \eta \frac{\partial L}{\partial b}
\]

其中，\(\eta\) 是学习率，控制了参数更新的步伐大小。

#### 学习率的选择与调整策略

学习率是梯度下降中一个非常关键的超参数。如果学习率过大，模型可能会在最小值附近震荡甚至发散；如果学习率过小，训练过程可能会非常缓慢，并且容易陷入局部最小值。

为了优化学习率的选择，可以采用如下策略：

- 学习率衰减：在训练过程中逐步减小学习率。
- 自适应学习率算法：例如 Adam、RMSprop 等，能够自动调整学习率。
- 使用学习率调度策略：根据损失函数的变化调整学习率。

这些策略有助于模型更快速地收敛至一个好的解，并提高训练的稳定性。

以上章节内容包含了反向传播算法的基础理论和核心概念。在接下来的内容中，我们将深入探讨如何将这些理论知识转化为实际的代码实现，并通过具体的编程实践来加深理解。

# 3. 反向传播算法的实践实现

## 3.1 编程环境和工具的搭建

### 3.1.1 选择合适的编程语言和框架

在实现反向传播算法之前，我们需要选择合适的编程语言和框架。当前，Python 作为数据科学和机器学习的首选语言，因其简洁的语法和丰富的库支持，成为了实现反向传播算法的热门选择。在Python中，我们有诸如TensorFlow、Keras和PyTorch等流行框架，它们提供了高度抽象的API来构建和训练神经网络，极大地简化了算法的实现过程。

TensorFlow 由Google开发，是一个开源的机器学习库，它提供了强大的计算图功能，非常适合实现复杂的模型。而Keras作为TensorFlow的高级API，专注于快速实验，能够更快地实现初步原型。

PyTorch由Facebook开发，它强调动态计算图，使得模型的设计和调试更加直观。由于其灵活性，PyTorch在研究社区中受到了广泛欢迎。

选择合适的框架不仅取决于个人喜好，还取决于项目的具体需求。对于需要高性能部署的项目，TensorFlow可能更受青睐；而在研究和原型开发阶段，PyTorch的易用性可能更受欢迎。

### 3.1.2 环境配置和依赖管理

搭建编程环境的第一步通常是安装Python解释器。然后，根据选择的框架，安装相应的库和依赖项。推荐使用`virtualenv`或`conda`这样的工具来创建隔离的环境，这样可以避免不同项目之间的依赖冲突。

使用`virtualenv`创建一个新的Python环境的步骤如下：

# 安装virtualenv
pip install virtualenv

# 创建一个新的虚拟环境
virtualenv myenv

# 激活虚拟环境
# Windows
myenv\Scripts\activate
# macOS/Linux
source myenv/bin/activate

# 安装依赖
p