【池化层解析】：图像识别降维与特征不变性的核心机制

# 1. 图像识别中的降维概念

在图像识别和机器学习领域中，降维是一个至关重要的步骤，它能够减少输入数据的维度，从而降低计算复杂性，同时还能增强模型对数据特征的提取能力。降维主要包含两个目的：一是为了简化数据结构，使数据易于处理；二是为了剔除冗余信息，增强模型的泛化能力。图像识别中的降维可以通过多种方法实现，例如主成分分析(PCA)、线性判别分析(LDA)等。然而，这些传统的降维方法往往忽视了图像数据的空间关联性，因此，在深度学习图像识别任务中，通常会采用池化层来实现降维，从而获得更为抽象的图像特征表示。

# 2. 池化层理论基础

### 2.1 池化层的数学原理

#### 2.1.1 信号处理与采样理论

池化层，作为一种图像识别技术中的关键组件，其工作原理深受信号处理与采样理论的影响。在数字信号处理中，采样理论告诉我们，如果一个信号的频率范围被限制在一个适当的值以内（通常称为奈奎斯特频率），那么理论上可以无损地从其样本中重构原始信号。池化操作可以类比为图像空间的一种降采样手段，通过减少数据的样本数来降低维度，同时保留重要的特征信息。在深度学习中，这种操作通常是以池化窗口（Pooling Window）的形式出现，通过设定适当的窗口大小和步长（Stride），可以在减少数据量的同时，最大限度地保留图像的主要特征。

#### 2.1.2 降维与信息压缩的关系

降维是数据处理领域中的一项基本技术，旨在减少数据的特征数量，同时尽可能保留数据中的有用信息。池化层操作是图像和信号处理中降维的一种实现方式。通过池化操作，高维数据被转换为低维数据，原始数据中的冗余被去除，数据的特征维度被压缩，从而使得后续的处理更加高效。在信息压缩的上下文中，池化层实现了局部区域特征的抽象和概括，它通过确定性或概率性的方法，为特征映射提供了一种结构化的压缩方式，使网络能够抓住图像的主要特征，丢弃不必要的变化。

### 2.2 池化层在神经网络中的作用

#### 2.2.1 特征提取的重要性

池化层是卷积神经网络（CNN）中用于特征提取的重要层次。它将图像划分为若干区域，并为每个区域计算出一个代表性的值，如最大值或平均值。这一操作使得网络能够对输入图像进行更加抽象的表示，从而提升网络对图像中的主要特征的感知能力。重要的是，池化操作使得网络具有了一定程度的平移不变性，即图像的轻微位置变动不会显著影响池化后特征的表示。这对于识别同一对象在不同位置的情况至关重要，使模型更加强大和鲁棒。

#### 2.2.2 池化层与全连接层的协同效应

池化层在CNN中与全连接层形成了有力的协同效应。在经过若干卷积层和池化层的处理后，图像数据被逐步转化为了高抽象级别的特征图，而这些特征图随后会输入到一个或多个全连接层，以进行最终的分类或回归任务。池化层减少了特征图的空间维度，这不仅减少了全连接层的参数数量，从而减轻了过拟合的风险，也加快了模型的训练和推理速度。此外，池化层还通过其不变性特性，有助于全连接层更好地捕捉全局特征，这是对局部特征进行有效整合的关键步骤。

### 2.3 池化层的主要类型

#### 2.3.1 最大池化和平均池化

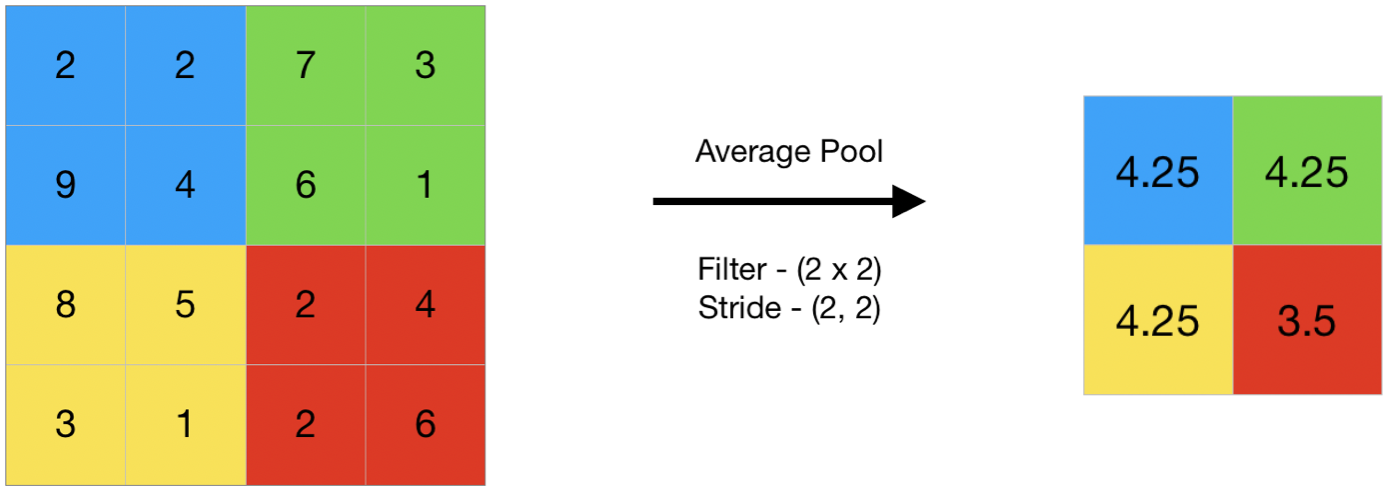
在众多池化策略中，最大池化（Max Pooling）和平均池化（Average Pooling）是两种最常用的池化类型。最大池化通过取池化窗口内的最大值作为输出，它强调了图像中最强的信号，有助于保留图像中显著的特征。平均池化则通过计算池化窗口内的平均值作为输出，它能够更好地保留图像的背景信息，减少数据的丢失。这两种池化方式在实际应用中各有优势，最大池化通常能够更好地保留特征的显著性，而平均池化在一些需要保留平滑特征的任务中效果更佳。

#### 2.3.2 其他池化策略简介

除了最大池化和平均池化之外，研究者还提出了其他多种池化策略。其中包括但不限于：随机池化（Stochastic Pooling），它通过随机选择池化窗口中的一个值作为输出，引入了额外的随机性，可以增强模型的泛化能力；分层池化（Hierarchical Pooling），它通过构建分层结构来学习数据的多级表示；还有空间金字塔池化（Spatial Pyramid Pooling），它在不同尺度上应用池化操作，用于捕捉不同大小的特征模式。这些不同的池化策略能够应对不同的网络架构和任务需求，展示了池化层在深度学习中的灵活性和多样性。

# 3. 特征不变性的理论与实践

## 特征不变性的定义
### 仿射变换与不变性
在图像识别和计算机视觉领域，特征不变性是指在图像经历了某种变换（如旋转、缩放、平移）后，关键特征仍能被识别和匹配的能力。仿射变换是一种二维坐标变换，它可以表示为一个矩阵乘以向量，包括旋转、缩放、平移和剪切等操作。

特征不变性的核心在于，它允许系统在面对目标位置、方向和形状的变化时，仍能够保持对同一目标的稳定识别。这种不变性能够显著提高系统的鲁棒性和泛化能力，是机器学习和深度学习中提升模型性能的关键技术之一。

### 不变性的数学模型
数学上，仿射变换可以通过线性变换矩阵和偏移向量来表示，形式化地描述了输入图像在进行一系列变换后，如何保持某些特征的不变性。例如，一个平移的仿射变换可以表示为：

\[
\begin{bmatrix}
x' \\
y'
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & t_x \\
0 & 1 & t_y
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
1
\end{bmatrix}
\]

其中，\((x, y)\) 是原始坐标，\((x', y')\) 是变换后的坐标，\(t_x\) 和 \(t_y\) 分别表示在 x 和 y 方向上的平移量。对于不同的仿射变换，变换矩阵会包含旋转、缩放等其他参数。

## 实现特征不变性的技术
### 数据增强方法
数据增强是通过一系列操作来人为扩充训练数据集的技术，是实现特征不变性的常用方法之一。常见的数据增强方法包括：

- **旋转**：对图像进行随机旋转操作，增强模型对旋转的鲁棒性。
- **缩放**：随机改变图像的大小，训练模型能够处理不同尺寸的目标。
- **剪切**：随机剪切图像的一部分，然后将剩余部分拼接，模拟目标在图像中的不同位置。

from imgaug import augmenters as iaa

# 定义一个图像增强顺序
seq = iaa.Sequential([
    iaa.Fliplr(0.5), # 随机水平翻转
    iaa.Affine(
        scale={"x": (0.8, 1.2), "y": (0.8, 1.2)},
        translate_percent={"x": (-0.2, 0.2), "y": (-0.2, 0.2)},
        rotate=(-45, 45)
    )