【nlminb参数选择全攻略】：选对算法，事半功倍

# 1. nlminb算法概述

nlminb算法是统计软件和编程语言中常用的非线性最小化工具，特别适合于处理复杂的非线性优化问题。它以数值优化的方式，通过迭代逼近最小值点，广泛应用于科学研究和工程领域。本章节我们将对nlminb算法进行一个初步了解，并简要介绍其应用场景和使用环境。这将为我们深入探讨其背后的数学原理和工作流程打下坚实的基础。

在接下来的章节中，我们将详细探索nlminb算法的原理、参数调优、实际应用挑战以及技术展望，引导读者深入理解并运用这一强大的算法工具。

# 2. 理解nlminb算法原理

在深入探讨nlminb算法的实战应用之前，我们需要先对其算法原理有一个全面且深刻的理解。nlminb算法是一种用于解决非线性最小化问题的数值优化算法，其在统计计算、机器学习、工程设计等多个领域有着广泛的应用。本章将会从数学基础、工作流程以及与其他优化方法的比较三个维度对nlminb算法原理进行阐释。

## 2.1 nlminb算法的数学基础

### 2.1.1 目标函数和约束条件

nlminb算法的核心目的是最小化一个给定的目标函数，这个目标函数是关于变量的非线性函数。在数学上，我们通常表示为寻找一组变量 \( \vec{x} = (x_1, x_2, ..., x_n) \)，使得目标函数 \( f(\vec{x}) \) 达到最小值。这里的 \( f \) 是非线性的，并且可能存在多个局部最小值。

除了目标函数外，实际问题中常常会有各种约束条件，如等式约束和不等式约束。等式约束通常表示为 \( g_i(\vec{x}) = 0 \)，不等式约束表示为 \( h_j(\vec{x}) \leq 0 \)，其中 \( i, j \) 表示约束条件的编号。

### 2.1.2 优化问题的数学模型

将上述问题形式化，我们得到如下数学模型：

\[
\begin{align*}
\text{minimize} & \quad f(\vec{x}) \\
\text{subject to} & \quad g_i(\vec{x}) = 0, \quad i = 1, 2, ..., m \\
& \quad h_j(\vec{x}) \leq 0, \quad j = 1, 2, ..., p
\end{align*}
\]

在实际问题中，\( m \) 和 \( p \) 分别代表等式和不等式约束的数量，而 \( \vec{x} \) 是我们需要求解的变量集合。

## 2.2 nlminb算法的工作流程

### 2.2.1 初始化和参数估计

nlminb算法开始时首先需要对变量进行初始化。初始化的方式可以是随机的，也可以是根据问题特性进行精心设计的。对于参数估计，算法需要设置初始值，比如梯度下降的步长、收敛容忍度等。

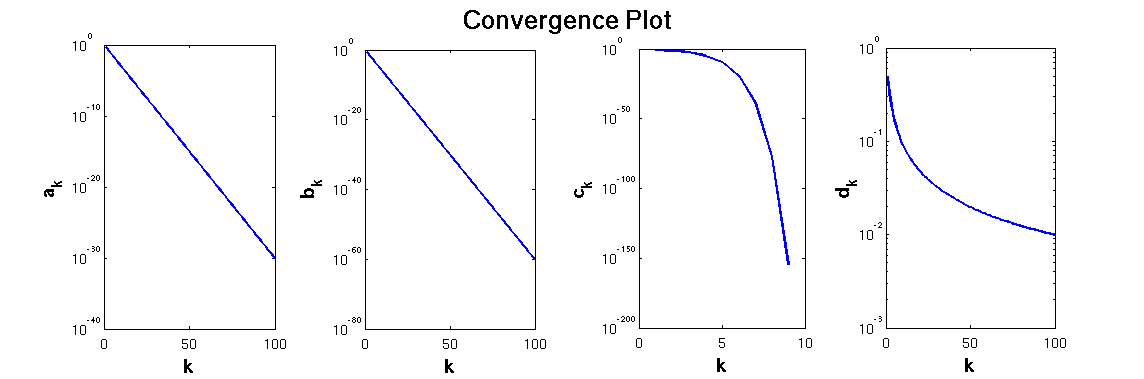
### 2.2.2 迭代过程与收敛性分析

算法会不断地通过迭代过程对变量进行更新以求解问题。在每一步迭代中，算法根据目标函数的梯度信息来决定更新的方向，并通过线搜索技术来确定合适的步长。迭代过程一直进行，直到满足终止条件，例如连续几次迭代中目标函数的改善小于某个阈值，或者达到预设的迭代次数上限。

### 2.2.3 结果输出和解释

当算法终止时，它会输出找到的最优解及其目标函数的最小值。这个解需要被仔细检查，以确保它是可行的（满足所有的约束条件）。对于一些有多个局部最小值的问题，得到的解可能是局部最优而非全局最优，此时算法的输出还需要结合具体问题的上下文来解释。

## 2.3 nlminb算法与其他优化方法的比较

### 2.3.1 与梯度下降法的对比

梯度下降法是一种简单的优化算法，通过迭代地沿目标函数的梯度负方向更新变量来求最小值。与梯度下降法相比，nlminb算法在处理带约束的优化问题上更为强大。另外，nlminb采用了更为复杂的迭代过程和更高级的线搜索技术来提高收敛速度。

### 2.3.2 与遗传算法的对比

遗传算法是一种模拟自然选择过程的全局优化算法，通过模拟生物进化中的遗传和自然淘汰机制来寻找最优解。nlminb算法与遗传算法的主要区别在于，nlminb更适用于求解连续变量的优化问题，并且在数学模型和收敛性方面提供了更多的保证。

### 2.3.3 与模拟退火算法的对比

模拟退火算法是一种随机优化算法，它借鉴了物理中固体物质冷却时的退火过程。与模拟退火相比，nlminb算法能更快速地收敛于局部或全局最优解，尤其是在解空间平滑且具有良好的梯度信息时。然而，nlminb在处理大规模问题时可能需要更高效的数值计算。

在下一章节中，我们将深入了解nlminb算法在参数调优上的具体实践，包括参数选择的重要性、调优技巧以及案例分析，让读者能够更好地掌握这一强大工具的实际应用。

# 3. nlminb算法的参数调优实践

## 3.1 参数选择的重要性
### 3.1.1 参数对算法性能的影响
在nlminb算法中，选择合适的参数对于确保算法性能至关重要。参数调整可以显著影响算法的收敛速度、稳定性和求解质量。例如，收敛性准则参数控制着算法何时停止迭代，而初始步长参数影响算法的探索能力。如果初始步长太大，算法可能会跳过最优解；如果太小，则可能导致算法收敛缓慢，甚至无法在合理时间内找到解。因此，理解各种参数的角色以及它们如何影响算法的性能是至关重要的。

### 3.1.2 参数调优的基本原则
在进行参数调优时，应该遵循一些基本原则。首先，理解问题的性质是关键，这有助于设定合理的参数起始值。其次，进行逐步调整，每次修改一个或少数几个参数，这样可以更容易地追踪哪些参数调整对性能产生了积极或消极的影响。第三，监控性能指标，如目标函数值的改善、迭代次数等，以便于评估当前参数设置的效果。最后，重复上述过程，直到达到满意的性能水平。

## 3.2 实践中的参数选择技巧
### 3.2.1 初始值的设定方法
初始值的设定通常取决于问题的特定背景。对于一些问题，可以使用经验法则来确定一个好的起点。在其他情况下，可以运行算法多次，每次使用不同的随机初始值，然后选择导致最佳结果的初始值。此外，也可以从问题的已知解或部分解出发，这样通常能够更快地收敛到全局最优解。

### 3.2.2 精细搜索和全局搜索的平衡
在nlminb算法中，搜索过程可以被分类为精细搜索和全局搜索。精细搜索专注于在当前解的邻域内寻找更好的解，而全局搜索则着眼于探索更广泛的解空间。这两种搜索方法在实践中需要平衡。过度的精细搜索可能导致算法陷入局部最优，而过度的全局搜索可能增加找到全局最优解的几率，但会增加计算成本。因此，合理选择这两个策略的参数比例是调优的关键。

### 3.2.3 步长和容忍