选择排序：揭秘其不高效背后的原理

# 1. 选择排序算法概述

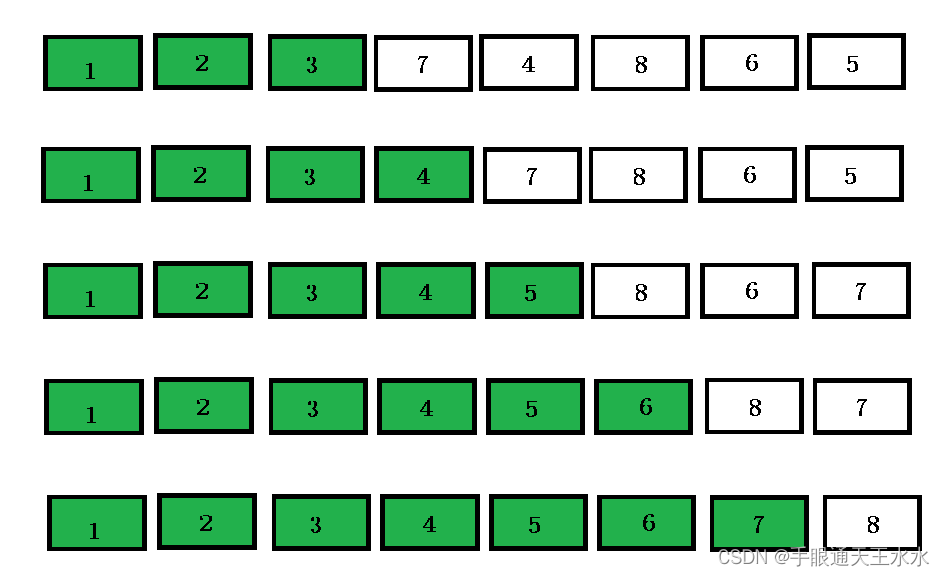
选择排序是一种简单直观的排序算法，它的工作原理是每次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。选择排序算法是不稳定的排序方法，它的比较次数和移动次数是独立于待排序数据的初始状态，对于n个数据的序列，需要进行`n*(n-1)/2`次比较和`n`次交换。

在选择排序的过程中，会出现一个中间步骤，即通过一系列的比较操作，找到一个未排序序列中的最小（或最大）元素，然后将其放到已排序序列的末尾。这一过程会重复执行，直到所有元素均被排序。

尽管选择排序的效率不是最优的，它的时间复杂度为O(n^2)，但它具有算法简单和容易实现的优点。在小规模数据的排序任务中，选择排序可以作为一种简单有效的选择。不过，在大规模数据处理时，我们往往需要更高效的排序算法，比如快速排序、归并排序等。接下来，我们将深入探讨选择排序的原理和实现细节。

# 2. 选择排序的基本原理

选择排序是一种简单直观的排序算法。其工作原理是：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

## 2.1 排序算法的分类与比较

### 2.1.1 排序算法的分类

排序算法可以分为内部排序和外部排序。内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中尚需对外存进行访问的排序。

内部排序算法包括：

- 插入排序：包括直接插入排序、二分插入排序、Shell排序等。
- 选择排序：包括简单选择排序、堆排序等。
- 交换排序：包括冒泡排序、快速排序等。
- 归并排序：包括二路归并排序、多路归并排序等。
- 基数排序。

### 2.1.2 常见排序算法性能比较

从时间复杂度、空间复杂度、稳定性和适应性等多个方面对常见排序算法进行比较。

**时间复杂度：**

- 平均时间复杂度：快速排序、归并排序、堆排序是O(nlogn)级别的，选择排序、冒泡排序是O(n^2)级别的。
- 最坏时间复杂度：插入排序、冒泡排序、选择排序在最坏情况下达到O(n^2)。
- 最好时间复杂度：堆排序在最好情况下也是O(nlogn)。

**空间复杂度：**

- 原地排序算法，空间复杂度为O(1)，如冒泡排序、选择排序、插入排序。
- 非原地排序算法，空间复杂度大于O(1)，如归并排序、快速排序。

**稳定性：**

- 稳定的排序算法，如冒泡排序、插入排序、归并排序。
- 不稳定的排序算法，如快速排序、选择排序、堆排序。

**适应性：**

- 适应性好的排序算法，如插入排序、冒泡排序、选择排序。
- 适应性差的排序算法，如快速排序、归并排序。

## 2.2 选择排序的核心思想

### 2.2.1 选择排序的定义

选择排序（Selection Sort）是一种简单直观的排序算法，它的工作原理如下：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

### 2.2.2 算法步骤详解

选择排序算法步骤如下：

1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
2. 从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾。
3. 重复步骤1、2，直到所有元素均排序完毕。

## 2.3 时间复杂度与空间复杂度分析

### 2.3.1 时间复杂度的计算

选择排序算法的时间复杂度分析通常基于比较次数和交换次数：

- **最坏情况**：当输入数组是反向顺序时，比较次数达到最大。
- **最好情况**：当输入数组已经是正序时，比较次数最少。
- **平均情况**：对于随机数据，平均比较次数为 `(n-1) * (n-2) / 2`。

由于选择排序每轮选择中都要进行一次遍历，因此算法的时间复杂度为 `O(n^2)`。

### 2.3.2 空间复杂度的评估

选择排序是一种原地排序算法，除了少数变量用于临时存储之外，不需要额外的存储空间，因此空间复杂度为 `O(1)`。

下面是一个选择排序算法的实现示例，以及对应的详细逻辑分析：

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        # 假定当前位置是最小值位置
        min_index = i
        for j in range(i+1, n):
            # 如果发现更小的值，则更新最小值位置
            if arr[j] < arr[min_index]:
                min_index = j
        # 将找到的最小值与当前位置元素交换
        arr[i], arr[min_index] = arr[min_index], arr[i]
    return arr

# 测试代码
array = [64, 25, 12, 22, 11]
sorted_array = selection_sort(array)
print("Sorted array:", sorted_array)

**逻辑分析：**

1. 初始化数组长度为 `n`。
2. 从数组的第一个元素开始，遍历整个数组。
3. 在每个位置假设当前元素是最小的，记录其索引为 `min_index`。
4. 遍历当前元素后面的所有元素，如果发现有比它小的元素，更新 `min_index`。
5. 如果 `min_index` 不等于当前遍历的起始位置 `i`，则交换这两个位置的元素。
6. 继续从下一个位置开始重复上述过程，直到整个数组排序完成。

由于选择排序只涉及对元素的交换操作，且这些操作是就地执行的，因此该算法的空间复杂度为 `O(1)`，时间复杂度为 `O(n^2)`。

在下一章节中，我们将深入探讨选择排序的实现细节，包括代码实现、优化技巧、以及常见问题的解决方法。

# 3. ```
# 第三章：选择排序的实现细节

选择排序算法的实现细节是其高效性能的体现。本章我们将详细探讨算法的代码实现、实现过程中可能遇到的问题以及其变体形式。

## 3.1 算法的代码实现

选择排序的基本代码实现相对简单，但想要让算法在特定的场景下表现得更优，代码上的优化和技巧是不可或缺的。

### 3.1.1 选择排序的基本代码框架

基本的选择排序算法实现可以用以下的伪代码表示：

function selectionSort(array):
    for i from 0 to array.length - 2:
        min_index = i
        for j from i + 1 to array.length - 1:
            if array[j] < array[min_index]:
                min_index = j
        swap array[i] with array[min_index]
    return array

通过该伪代码，我们可以观察到算法的基本结构是两层循环：外层