计数排序原理与应用：探索非比较排序的极致优势

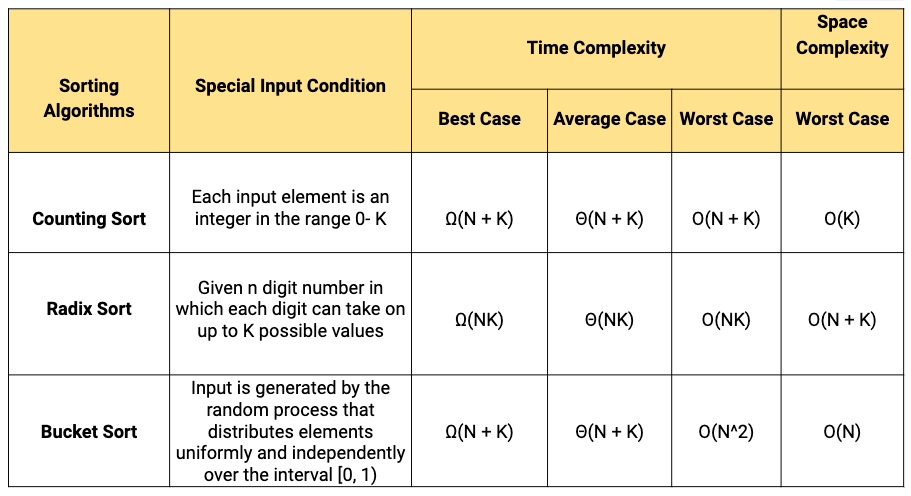
# 1. 计数排序的基本原理

计数排序（Counting Sort）是一种非比较型的排序算法，适用于一定范围内的整数排序。在计数排序中，我们创建一个额外的数组C，其大小等于待排序数组A中的最大值K加一。数组C的索引用于表示待排序数组中每个元素的出现次数。通过填充数组C并进行累加，我们可以确定每个元素在排序数组中的正确位置。

## 算法步骤

1. 找出数组中的最大值和最小值，确定计数数组C的范围。
2. 初始化计数数组C，使其所有值为0。
3. 遍历待排序数组A，统计每个元素的出现次数并填充到计数数组C中。
4. 根据计数数组C，确定每个元素在排序后的数组中的正确位置。
5. 通过反向填充计数数组C，得到最终的排序结果。

计数排序的这种处理方式决定了它在面对大规模数据时的效率。与基于比较的排序算法不同，计数排序的时间复杂度为O(n+k)，其中n是待排序数组的元素数量，k是数据范围的大小。因此，当k不是特别大时，计数排序的效率非常高。

def counting_sort(arr, min_value, max_value):
    # 初始化计数数组
    count = [0] * (max_value - min_value + 1)
    output = [0] * len(arr)
    # 计算每个元素的出现次数
    for num in arr:
        count[num - min_value] += 1
    # 累加计数数组，确定元素的正确位置
    for i in range(1, len(count)):
        count[i] += count[i - 1]
    # 反向填充输出数组
    for num in reversed(arr):
        output[count[num - min_value] - 1] = num
        count[num - min_value] -= 1
    # 复制排序后的结果到原数组
    for i in range(len(arr)):
        arr[i] = output[i]
    return arr

上例中，`counting_sort`函数展示了如何通过计数排序算法对整数数组进行排序。注意，该算法假设输入数组中的元素都在`min_value`和`max_value`之间。

# 2. 计数排序算法的理论分析

## 2.1 计数排序的时间复杂度和空间复杂度

### 2.1.1 理解线性时间复杂度的优势

计数排序算法的时间复杂度为O(n+k)，其中n表示输入数据的数量，k表示数据的范围。在最理想的情况下，当k较小且接近n时，计数排序的时间复杂度几乎接近于O(n)，这使得它在特定条件下远比具有O(nlogn)时间复杂度的比较排序算法更高效。这种线性时间复杂度的优势尤其体现在数据范围有限、数量巨大的场景中。

### 2.1.2 分析计数排序的空间使用情况

计数排序的空间复杂度为O(k)。它需要一个额外的计数数组来存储每个整数出现的次数，这个计数数组的大小直接与数据的范围k相关。因此，对于数据范围非常大的情况，计数排序可能会消耗大量内存。然而，当k较小的时候，这种空间开销是可以接受的，这也是计数排序在实际应用中的一个重要考量点。

## 2.2 计数排序的稳定性分析

### 2.2.1 排序算法稳定性的定义

稳定性是排序算法的一个重要特性。如果一个排序算法能够保证相等的元素在排序后的相对位置不改变，那么这个算法就是稳定的。稳定排序算法在处理具有相同键值的记录时尤其有用，例如在数据库中按照多个字段排序。

### 2.2.2 计数排序的稳定性证明与例子

计数排序是稳定的排序算法。其稳定性主要来自于计数数组的构造方式，以及在填充输出数组时的处理方法。在计数排序算法中，对于每个待排序的元素，我们根据其值先查找计数数组，然后再将它放到输出数组的正确位置上。即使两个元素的计数相同，我们也能保证它们按照原始输入顺序进行排序。例如，如果两个元素都是5，且第一个5在原始数据中出现在第二个5之前，那么在排序后的数组中，第一个5仍然会出现在第二个5前面。

## 2.3 计数排序与其他排序算法的比较

### 2.3.1 与比较排序算法的对比

比较排序算法，如快速排序、归并排序等，都有O(nlogn)的时间复杂度下限。计数排序在O(n+k)的时间复杂度下能够更快地处理非负整数序列，特别是当数据范围k相对于n不是特别大时。然而，计数排序并不适用于包含大量不同值的大型数据集，这时候比较排序算法的O(nlogn)时间复杂度更加适合。

### 2.3.2 非比较排序算法间的优劣分析

除了计数排序外，非比较排序算法还包括基数排序和桶排序。这些算法在处理特定类型的数据集时可能比计数排序表现得更好。例如，基数排序适用于处理具有多关键字的记录，而桶排序适用于数据分布均匀的场景。计数排序的优劣很大程度上取决于输入数据的特性，如数据范围和数据集大小。在选择合适的排序算法时，需要综合考虑这些因素。

graph TD;
    A[开始] --> B[输入数据]
    B --> C{数据范围与数据量}
    C -->|数据范围小| D[使用计数排序]
    C -->|数据范围大| E[使用比较排序]
    C -->|数据分布均匀| F[使用桶排序]
    C -->|多关键字记录| G[使用基数排序]
    D --> H[排序完成]
    E --> H
    F --> H
    G --> H

通过上述分析，我们可以看出计数排序的时间和空间复杂度及其稳定性特点，这有助于我们更好地理解计数排序在多种排序算法中的定位和应用范围。在实际开发中，选择合适的排序算法往往需要根据具体的数据特性和需求来决定。

# 3. 计数排序的实践应用

## 3.1 计数排序在数据预处理中的应用

### 3.1.1 数据去重和频率统计

计数排序是用于整数排序的一种非比较型算法，其核心思想是利用数组下标来确定元素的正确位置。这种排序方法适用于一定范围内的整数排序，在数据预处理中，它可以用来快速去重和频率统计。

为了实现数据去重和频率统计，可以采用计数排序的变种——基数排序。基数排序可以将数据分布到多个桶中，每个桶中的数据代表了一定范围内的整数，然后再通过从低位到高位进行排序，最终达到去重和排序的目的。具体操作步骤如下：

1. 创建一个足够大的数组来存放数据的频率，初始化为0。
2. 遍历原始数据，对每个元素，增加对应数组下标（即数据值）的计数。
3. 再次遍历数组，此时遍历的是数组，输出计数不为0的元素，即为去重后的数据。

在实际应用中，这种方法可以有效地对大量数据进行预处理，特别是在处理日志数据、网络流量分析等场景中有着出色的表现。

### 3.1.2 大数据量的快速排序预处理

当数据量非常大时，传统的排序算法如快速排序、归并排序等，其性能会受到递归调用和数据移动次数的限制。计数排序可以应用于这些场景，特别是在预处理阶段，为后续的排序提供支持。

应用计数排序进行大数据量的预处理，可以减少实际排序算法的运行时间。操作步骤如下：

1. 确定数据的范围，并根据这个范围初始化计数数组。
2. 遍历待排序的数据，统计每个元素出现的次数。
3. 根据计数数组，生成有序的元素序列，实现快速排序预处理。

由于计数排序的时间复杂度为O(n+k)（其中n是数据的个数，k是数据的范围），对于大数据量且k不是很大的情况，计数