冒泡排序：不仅仅是入门，实用场景及优化全攻略

# 1. 冒泡排序算法基础

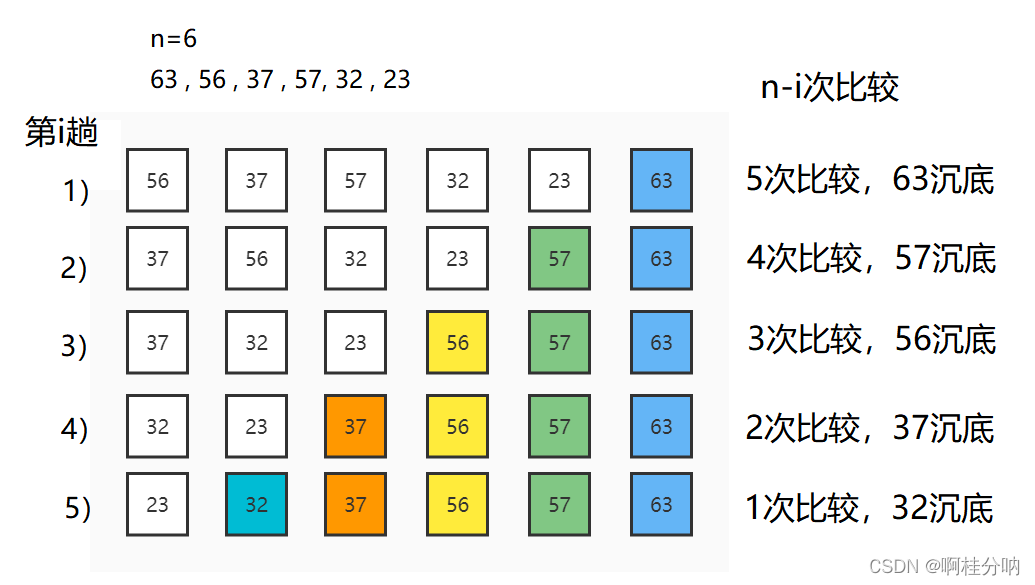
冒泡排序是一种简单直观的排序算法，因其在排序过程中通过相邻元素的比较与交换，使得较大的元素逐渐“冒泡”到数列的顶端而得名。该算法的基础思想是重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。

## 1.1 算法起源和名称由来

冒泡排序的起源可以追溯到1956年，由伊萨克·本尼迪克特·康威提出。之所以叫冒泡排序，是因为在排序过程中，较小的元素逐渐“上升”到数组的前端，而较大的元素则逐渐“下沉”到数组的后端，就像水中的气泡一样。

## 1.2 算法步骤和基本原理

冒泡排序通过一系列的“冒泡”操作，每次遍历都比较相邻的元素，如果它们的顺序错误，则交换这两个元素。这一过程会重复进行，直到没有任何一对数字需要交换，这意味着数列已经排序完成。尽管这个算法容易理解，但在处理大量数据时，其效率相对较低。

// 冒泡排序的伪代码示例

procedure bubbleSort( A : list of sortable items )
    n = length(A)
    repeat
        swapped = false
        for i = 1 to n-1 inclusive do
            if A[i-1] > A[i] then
                swap(A[i-1], A[i])
                swapped = true
            end if
        end for
        n = n - 1
    until not swapped
end procedure

上述伪代码展示了冒泡排序算法的基本步骤，其中`swapped`变量用于标记数组是否进行过交换操作，如果在某一轮遍历中没有发生任何交换，说明数列已经有序，算法可以提前结束。

# 2. 冒泡排序的理论与实践

### 2.1 算法理论分析

#### 2.1.1 排序的基本概念和原理

排序算法在计算机科学中扮演着核心的角色，是将一系列数据按照一定的顺序重新排列的过程。排序的基本目的是使数据序列变得有序，从而便于搜索、分析、压缩等后续处理。冒泡排序作为一种简单的排序算法，其基本思想是通过重复遍历待排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。

冒泡排序的基本原理是利用了比较和交换的方式，通过重复地遍历和比较，将数值较大的元素像水中的气泡一样“浮”到数列的顶端。直观上理解，可以想象成一个高度不断减少的气泡柱，气泡会逐渐上升到顶端。

#### 2.1.2 冒泡排序的时间复杂度与空间复杂度

在分析算法性能时，时间复杂度和空间复杂度是两个非常重要的指标。冒泡排序的时间复杂度主要取决于两个因素：数据的初始排列状态和冒泡过程中最坏情况的比较次数。

在最坏的情况下，也就是每次遍历都需要进行最大次数的比较和交换，时间复杂度为O(n^2)，其中n是数列的长度。这是因为冒泡排序需要两层嵌套循环来完成排序任务。空间复杂度相对较低，因为冒泡排序是一种原地排序算法，不需要额外存储空间，空间复杂度为O(1)。

### 2.2 算法实现步骤

#### 2.2.1 基本冒泡排序过程

基本冒泡排序过程涉及到两个主要步骤：

1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个。
2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

重复以上的步骤，每次迭代都将未排序序列的最大数“冒泡”到数列的顶端，直到整个数列变得有序。

#### 2.2.2 冒泡排序的代码实现

下面是一个基本的冒泡排序算法的代码实现示例，使用Python语言：

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

# 测试冒泡排序
arr = [64, 34, 25, 12, 22, 11, 90]
sorted_arr = bubble_sort(arr)
print("Sorted array is:", sorted_arr)

### 2.3 算法的正确性验证

#### 2.3.1 逻辑错误与调试方法

算法实现完成后，确保其正确性是至关重要的。对于冒泡排序，验证其正确性可以通过多种方法进行，包括但不限于：

- 单元测试：编写多个测试用例来覆盖所有可能的情况，如空数组、只包含一个元素的数组、已经有序的数组、完全逆序的数组等。
- 日志记录：在排序过程中添加日志语句，跟踪排序步骤，以便检查每一步是否正确执行。
- 调试器：使用调试工具逐行执行代码，观察变量的变化，确保逻辑正确性。

#### 2.3.2 排序结果的测试与验证

测试冒泡排序的正确性除了逻辑验证之外，还需要验证最终的排序结果。以下是几个测试案例：

# 测试案例
assert bubble_sort([1, 2, 3, 4, 5]) == [1, 2, 3, 4, 5], "测试案例1失败"
assert bubble_sort([5, 4, 3, 2, 1]) == [1, 2, 3, 4, 5], "测试案例2失败"
assert bubble_sort([]) == [], "测试案例3失败"
assert bubble_sort([2]) == [2], "测试案例4失败"
assert bubble_sort([1, 3, 2, 5, 4]) == [1, 2, 3, 4, 5], "测试案例5失败"

通过上述测试案例，我们能够验证冒泡排序算法的正确性。如果所有的断言测试都通过，我们可以较为确信算法实现是正确的。

# 3. 冒泡排序的优化策略

冒泡排序，尽管在效率上不总是最佳选择，但它的简单性和教学价值使得研究其优化策略具有深远的意义。我们已经了解到冒泡排序的基本工作原理，现在是时候探讨如何使它更高效了。

## 3.1 优化算法性能

### 3.1.1 算法优化的基本原则

对于任何算法来说，最核心的优化原则之一是减少不必要的计算。在冒泡排序中，这通常意味着减少比较和交换的次数。基本冒泡排序会遍历数组多次，即使数组已经部分或完全排序。因此，优化的第一个思路是设置一个标志位，检查在一次完整的遍历中是否发生了交换，如果没有发生交换，说