【R语言t.test：实战应用】：9个案例教你如何快速入门并精通

# 1. R语言中的t.test基础

## 1.1 t.test入门
在数据科学与统计分析的世界里，t.test是不可或缺的工具之一。它是一种统计假设检验，用于比较两个或多个组的均值是否存在显著差异。R语言作为一门专为统计计算设计的编程语言，为用户提供了强大的t.test函数来执行这一检验。初学者往往会从R语言提供的基础函数开始，逐步深入理解其背后的统计原理和应用技巧。

## 1.2 R语言与t.test的兼容性
R语言的灵活性和开源性使其成为进行t.test等统计分析的首选。由于R语言拥有丰富的包和函数库，这使得它在进行数据分析时能够快速响应研究者的不同需求。其中，t.test函数的简便性和功能性，使其成为数据分析初学者和专业统计师的共同选择。在这一章中，我们将着重介绍如何在R语言环境中使用t.test，以及它的基本功能和参数解释。

# 2. t.test的理论基础与R语言实现

### 2.1 t.test的理论背景

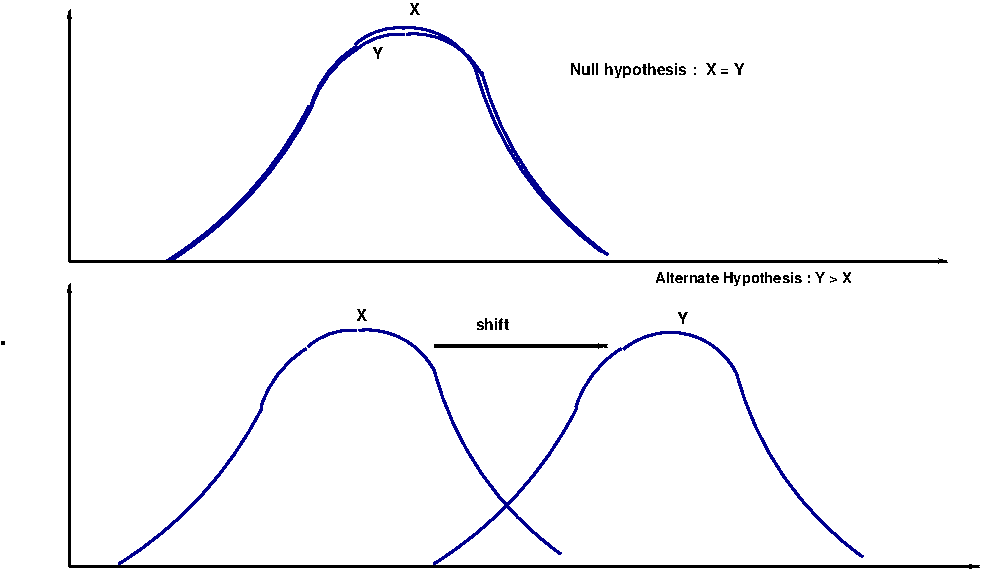
#### 2.1.1 假设检验与t检验

在统计学中，假设检验是一种用于评估关于总体参数的统计假设的决策过程。它是数据分析中的核心工具，广泛应用于科学研究和工业界。t检验是假设检验的一种，主要用于评估两个样本均值是否存在显著性差异，或样本均值是否与已知总体均值存在显著性差异。t检验假设样本数据来自正态分布，并且总体标准差未知。

**参数检验的限制**：

- **数据量小**：当样本量小于30时，由于中心极限定理的限制，样本均值可能不符合正态分布。
- **总体标准差未知**：在实际应用中，总体的标准差往往是未知的，这限制了z检验的使用。

**t检验的优点**：

- **适用范围广**：适用于小样本数据，不要求总体方差已知。
- **灵活性强**：可以进行单样本、双样本独立和配对样本t检验。

#### 2.1.2 t分布的特点与应用

t分布是由William Sealy Gosset以笔名“Student”发表的，因此t检验常被称为“Student's t-test”。t分布是一种以样本均值的分布为基础的概率分布，其形状由自由度决定，当自由度增加时，t分布的形状趋于正态分布。

**t分布的主要特点**：

- **单峰**：与正态分布相似，t分布也是单峰的。
- **对称**：关于均值对称。
- **尾部**：比正态分布有更厚的尾部，即极端值出现的概率更高。

在数据分析中，t分布主要应用于小样本数据的均值差异检验。当样本量较小时，t分布提供了比正态分布更为准确的推断依据。随着样本量的增加，t分布会接近正态分布，这也是为什么在大样本量的情况下，t检验和z检验结果非常接近的原因。

### 2.2 t.test函数的参数解析

#### 2.2.1 参数选择与意义

在R语言中，t检验可以通过`t.test()`函数实现。该函数提供了多种参数供用户选择，以适应不同的数据分析场景。

**基本参数**：

- `x`：一个数值向量，或者是第一个样本的数据。
- `y`：一个数值向量，表示第二个样本的数据。如果只提供`x`，则执行单样本t检验。
- `alternative`：检验的备择假设类型，可以是`"two.sided"`（双尾），`"less"`（左侧），或`"greater"`（右侧）。
- `mu`：在单样本t检验中，`mu`用于指定检验的总体均值。
- `paired`：逻辑值，指定是否进行配对样本t检验。

# 示例代码：单样本t检验
single_sample <- t.test(x = sample_data, mu = 50, alternative = "two.sided")

**参数意义分析**：

- `x`和`y`参数为t检验提供了实际数据来源。
- `alternative`参数决定了检验的类型，影响最终的统计决策。
- `mu`参数允许用户自定义检验的总体均值，为单样本t检验提供了更多灵活性。
- `paired`参数允许用户执行配对样本t检验，当`paired = TRUE`时，R会自动计算配对差值，并进行配对样本t检验。

#### 2.2.2 不同类型的t.test：独立样本与配对样本

在R语言中，`t.test()`函数可以灵活地处理不同类型的t检验。

**独立样本t检验**：

- 用于比较两个独立样本的均值是否存在显著性差异。
- 需要设置`alternative`参数为`"two.sided"`、`"less"`或`"greater"`。
- 示例代码已展示。

**配对样本t检验**：

- 用于比较两个相关样本的均值差异，例如重复测量数据。
- 设置`paired = TRUE`，R会处理配对样本的差异值。
- 示例代码：

# 示例代码：配对样本t检验
paired_sample <- t.test(x = sample_data1, y = sample_data2, paired = TRUE)

### 2.3 R语言中的t.test案例剖析

#### 2.3.1 单样本t检验案例

在单样本t检验中，我们通常检验一个样本的均值是否与已知的总体均值存在显著性差异。假设我们有一组学生的考试成绩数据，我们想检验平均成绩是否显著低于60分。

# 数据准备
set.seed(123)
student_scores <- rnorm(30, mean = 55, sd = 10)

# 进行单样本t检验
test_result <- t.test(student_scores, mu = 60, alternative = "less")

# 输出t检验结果
print(test_result)

**逻辑分析**：

- 我们首先使用`rnorm()`函数生成了30个服从正态分布的学生分数样本。
- 接着，我们使用`t.test()`函数执行了单样本t检验，检验学生的平均成绩是否显著小于60分。
- 输出的结果包括t值、自由度、p值等统计信息，我们可以据此作出统计决策。

#### 2.3.2 双样本t检验案例

在双样本t检验中，我们比较两个不同组别数据的均值差异。假设我们进行了一个实验，一组受试者使用某药物，另一组使用安慰剂，我们想要检验药物效果是否显著。

# 数据准备
drug_group <- c(22, 25, 21, 23, 22, 26, 27, 24, 28, 22)
control_group <- c(20, 19, 23, 21, 20, 18, 20, 19, 21, 20)

# 进行双样本t检验
two_sample_test <- t.test(drug_group, control_group, var.equal = TRUE)

# 输出t检验结果
print(two_sample_test)

**逻辑分析**：

- 我们创建了两个样本向量，分别代表药物组和对照组。
- 在`t.test()`函数中，我们指定了`var.equal = TRUE`，因为我们假设两个样本具有相同的方差。
- 输出的结果将给出两组均值是否存在统计学上显著差异的证据。

通过这些案例，我们可以看到t检验在实际数据分析中的应用和效果。接下来的章节将深入探讨t检验在数据分析中的实战应用和高级技巧。

# 3. t.test在数据分析中的实战应用

## 3.1 数据探索与假设检验

### 3.1.1 数据的初步探索方法

在进行任何正式的统计分析之前，数据探索是必不可少的一个步骤。数据探索可以帮助我们理解数据集的特征，如数据的分布、中心趋势、离散程度等。在R语言中，我们可以使用多种方法来执行数据探索。

首先，使用`summary()`函数可以得到数据集的一些基本描述性统计量，例如均值、中位数、四分位数等。其次，`hist()`函数用于绘制直方图，帮助我们观察变量的分布情况。另外，`boxplot()`函数可以绘制箱线图，用于发现异常值和比较不同组数据的分布情况。最后，`pairs()`函数可以生成一个矩阵，展示多个变量之间的关系。

这些方法可以让我们在进行假设检验前，对数据有一个全面的了解。例如，通过直方图我们可能发现数据不符合正态分布的假设，这将指导我们后续使用非参数检验方法。

# 加载数据集
data("mtcars")
# 数据描述性统计
summary(mtcars)
# 绘制直方图
hist(mtcars$mpg, breaks = 10, main = "Histogram of MPG", xlab = "Miles per Gallon")
# 绘制箱线图
boxplot(mtcars$mpg ~ mtcars$am, xlab = "Transmission", ylab = "Miles per Gallon", main = "Boxplot of MPG by Transmission")
# 多变量关系图
pairs(mtcars)

### 3.1.2 如何构建假设检验

假设检验是统计推断中的一个重要步骤，用于确定结果是否具有统计学意义。在t.test中，构建假设检验主要涉及两个假设