R语言：t.test高级技巧，让你的数据分析更上一层楼

# 1. t.test函数的原理和基本用法

在统计学中，t.test是一个非常重要的假设检验工具，它主要用于比较两组数据的均值是否存在显著性差异。这一方法由威廉·西利·戈塞特（William Sealy Gosset）首次提出，他化名为“学生”（Student），因而该方法也被称为学生t检验。

## 1.1 t.test的基本原理

t.test的基础是t分布，当样本量较小时，t分布可以看作是标准正态分布的一种近似。该检验的假设前提包括样本独立且同分布，样本数据来源于正态分布或近似正态分布，且方差未知。t.test通过计算t值和查找相应的t分布表，来确定两组数据均值差异的显著性。

## 1.2 t.test的基本用法

在R语言中，`t.test()`函数是实现t检验的工具。一个简单的单样本t检验可以用以下代码表示：

t.test(x, mu = 0)

这里`x`是你要测试的数据向量，`mu`是你要检验的假设均值。这将返回一个包含t值、自由度、p值等统计信息的对象，帮助判断两组数据均值之间是否存在显著差异。

通过上述内容，我们可以了解到t.test函数的原理以及如何在R中执行基本的t检验。接下来的章节将进一步探讨t.test的高级参数和应用，以加深对t检验技术的理解和应用能力。

# 2. t.test的参数详解和高级应用

t.test函数在统计学中是一个非常重要的工具，它主要用于两个样本均值的假设检验。为了深入理解并有效运用t.test，我们需要详细探讨其参数及其高级应用方法。

### 2.1 t.test的参数详解

t.test函数中的参数允许用户设定不同的条件来进行各种统计检验，如均值检验、置信区间设定以及备择假设的选择等。

#### 2.1.1 mean：假设均值的参数

`mean`参数允许用户设定一个期望的均值，该参数通常用于单样本t检验中。通过设置`mean`，我们可以对一个样本的均值进行假设检验，以判断它是否显著地偏离了我们所设定的期望均值。

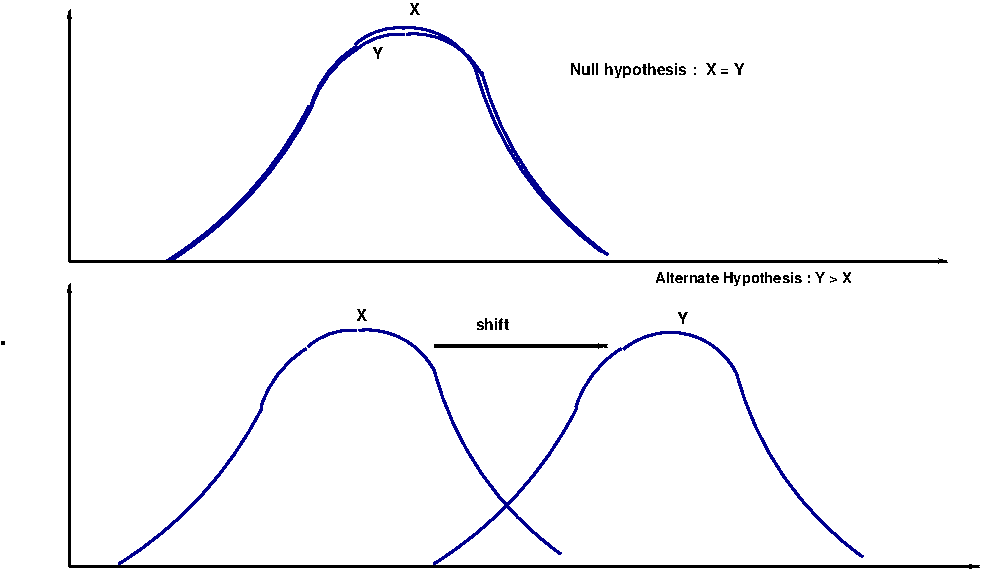
#### 2.1.2 alternative：备择假设类型

在进行t检验时，我们需要确定检验的类型，即备择假设`alternative`的设定。备择假设分为三种类型：

- `"two.sided"`：双尾检验，检验两样本均值是否存在显著差异。
- `"less"`：左尾检验，检验第一样本均值是否小于第二样本均值。
- `"greater"`：右尾检验，检验第一样本均值是否大于第二样本均值。

选择合适的备择假设是根据具体的研究目的和背景来进行的。

#### 2.1.3 conf.level：置信区间的设定

`conf.level`参数用于设定所估计的置信区间的置信水平，通常的取值有0.90、0.95和0.99。置信水平越高，我们对均值估计的信心越足，但相应的置信区间也会越宽。

### 2.2 t.test的高级应用

t.test的高级应用包括配对样本t检验、单样本t检验、两独立样本t检验等，这些检验类型能够满足不同场景下的统计需求。

#### 2.2.1 配对样本t检验

配对样本t检验适用于同一组样本在两个不同条件下的均值差异检验。在进行配对样本t检验时，通常需要在t.test函数中设置`paired=TRUE`。配对样本检验能够消除个体差异的干扰，更准确地反映处理因素的效果。

#### 2.2.2 单样本t检验

单样本t检验用于检验一个样本的均值是否显著异于某个预设的理论值。在实际操作中，我们通过设置`mu`参数来指定这个理论均值，随后t.test函数会返回这个样本均值的统计检验结果。

#### 2.2.3 两独立样本t检验

当需要比较两个独立样本的均值是否存在显著差异时，会使用两独立样本t检验。在调用t.test函数时，需要保证两个样本是独立的，并且它们来自正态分布，方差相等的总体。

### 代码块与逻辑分析

为了深入理解t.test函数的高级应用，这里给出一个两独立样本t检验的R语言示例代码，并进行详细分析：

# 假设有两组样本数据x和y
x <- c(2.9, 3.0, 2.5, 2.6, 3.2)
y <- c(3.8, 2.7, 4.0, 2.4)

# 进行两独立样本t检验
t.test(x, y, var.equal=TRUE)

在上述代码中，首先定义了两个向量`x`和`y`，分别代表两组独立样本数据。接着使用`t.test`函数对这两组数据进行独立样本t检验，其中`var.equal=TRUE`表示假定两组样本的方差相等。该函数会返回一个包含t统计量、自由度、p值和置信区间等信息的列表。

### 表格与数据分析

为了更直观地展示t.test的结果，我们可以使用R语言中的数据框（data.frame）来存储t.test的结果，并通过表格形式进行展示：

# 执行t.test并获取结果
test_result <- t.test(x, y, var.equal=TRUE)
# 将结果转换为数据框
result_table <- data.frame(
  Estimate = c(test_result$estimate),
  Conf_int = paste("[", round(test_result$conf.int, 2), "]", sep=""),
  t_stat = round(test_result$statistic, 2),
  p_value = test_result$p.value
)
result_table

上述代码首先执行了t.test，并将结果保存在`test_result`中。然后，通过`data.frame`创建了一个新的数据框`result_table`，其中包含了均值估计、置信区间、t统计量和p值等信息。通过这种方式，我们可以很方便地以表格形式输出和分析t.test的结果。

# 3. t.test在数据处理中的实践应用

在数据科学领域，t.test是一个非常重要的统计学工具，它能够帮助研究者检验两组数据的均值是否存在显著差异。在本章节中，我们将探讨t.test在数据处理中的实际应用场景，从数据预处理到统计分析项目的实践应用，再到结果的解读和应用。我们会用具体的代码示例来演示如何运用t.test进行数据分析，并通过实际案例来加深理解。

## 3.1 数据预处理

### 3.1.1 数据清洗

数据清洗是数据分析的第一步，也是至关重要的一步。在实际操作中，数据往往包含错误、缺失值或者不一致的情况，这些都需要在进行t.test之前先行处理。在R语言中，我们可以使用`na.omit()`函数来移除含有N