C++渲染引擎架构设计：构建可扩展系统的必修课

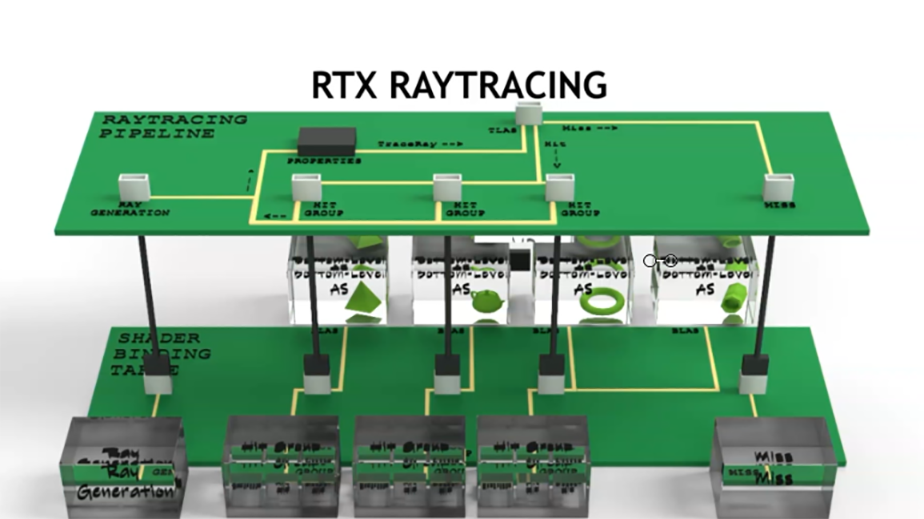
# 1. C++渲染引擎架构设计概述

在第一章中，我们将概述C++渲染引擎架构设计的基本原则和重要性。C++渲染引擎作为图形应用程序的核心，负责将3D模型、纹理、光照等元素转换为2D图像。为了实现高效和可扩展的渲染效果，本章将从宏观角度介绍渲染引擎的设计原则。

## 1.1 C++渲染引擎架构设计的重要性

C++渲染引擎是高性能图形应用的关键，其设计需要兼顾性能、可维护性和可扩展性。一个好的渲染引擎架构可以简化复杂的渲染流程，提高渲染效率，并为未来的技术更新和功能扩展提供便利。

## 1.2 架构设计的核心要素

一个优秀的渲染引擎架构包含多个关键要素，比如渲染流程的模块化、资源管理的高效性、以及支持多种渲染技术的可扩展性。在本章中，我们将探讨如何构建一个合理的架构框架，以及如何选择合适的图形API和渲染技术。

## 1.3 C++在渲染引擎中的应用

作为高效、接近系统底层的编程语言，C++在渲染引擎开发中扮演了核心角色。我们将在本章讨论C++的特性，如内存管理、面向对象编程等，以及它们如何在渲染引擎设计中发挥作用。

通过对渲染引擎架构设计的初步了解，为后续章节中深入探讨图形渲染管线、核心算法、可扩展系统设计策略、以及跨平台开发打下坚实的基础。

# 2. 渲染引擎理论基础

### 2.1 图形渲染管线详解

渲染管线（Graphics Pipeline）是图形学中的一个核心概念，它定义了3D模型从几何到最终像素显示于屏幕上的整个处理流程。管线中每个阶段的操作都对最终图像的渲染效果有着直接或间接的影响。

#### 2.1.1 渲染管线各阶段功能

图形渲染管线可以分为多个阶段，每个阶段都承担着特定的任务：

- **应用阶段（Application Stage）**：在此阶段，程序员通过API（如OpenGL, DirectX等）发送命令和数据给GPU。主要任务包括场景的设置、视图变换、剔除等。
- **几何处理阶段（Geometry Processing Stage）**：该阶段包括顶点着色器（Vertex Shader）、曲面细分着色器（Tessellation Shader）、几何着色器（Geometry Shader）和裁剪（Clipping）、屏幕映射（Screen Mapping）等。它负责将三维世界坐标转换为屏幕上的二维坐标，并且进行各种几何变换。
- **光栅化阶段（Rasterization Stage）**：将几何处理后的图形转化为屏幕上的一组像素。在此过程中，会进行深度测试（Depth Testing）、模板测试（Stencil Testing）等操作。
- **像素处理阶段（Pixel Processing Stage）**：包括片段着色器（Fragment Shader）和混合（Blending）。此阶段决定像素最终的颜色值。

graph LR
A[应用阶段] --> B[几何处理阶段]
B --> C[裁剪和屏幕映射]
C --> D[光栅化阶段]
D --> E[片段着色器]
E --> F[混合]
F --> G[最终像素颜色输出]

#### 2.1.2 图元处理与栅格化过程

在光栅化过程中，几何图形（通常是三角形）被处理为一系列的图元（如像素）。光栅化阶段的核心任务就是将这些图元映射到屏幕坐标系中，这个过程涉及到图元覆盖的屏幕像素的确定，以及对这些像素的属性（颜色、纹理坐标等）进行计算。

在这个过程中，GPU执行如下关键操作：

- **扫描转换（Scan Conversion）**：将三角形的边缘转换为像素坐标，并标记哪些像素在三角形内部。
- **插值（Interpolation）**：在三角形内部的像素上插值顶点的属性值，如颜色、纹理坐标、法线等。
- **Z-Buffer测试（Z-Buffer Testing）**：解决遮挡问题，确保最近的图元能够覆盖远的图元。

### 2.2 渲染技术的分类与应用

渲染技术的选择将直接影响到渲染引擎的性能和效果。根据不同的场景和需求，选择合适的渲染技术是非常关键的。

#### 2.2.1 光栅化渲染与光线追踪

- **光栅化渲染（Rasterization Rendering）**：它是实时图形渲染中最常见和最高效的技术。其主要思想是将3D场景中的几何体转换成2D图像时，忽略复杂的光学现象，仅计算几何体的边缘和表面。

光栅化渲染通常适用于实时渲染，比如视频游戏和交互式应用。它通过一系列优化手段（如Mipmapping、LOD技术、遮挡剔除等）提高渲染效率。

- **光线追踪（Ray Tracing）**：该技术模拟光线传播和物体交互的真实物理过程。光线追踪能够创建高度逼真的渲染效果，如全局光照、柔和阴影和反射。

由于其计算成本较高，传统上光线追踪主要用于离线渲染场景（如电影制作）。但随着技术的发展，实时光线追踪正变得越来越流行。

#### 2.2.2 实时渲染与离线渲染

- **实时渲染（Real-time Rendering）**：它以足够高的帧率（通常为每秒30帧以上）在屏幕上渲染图像，以达到动画效果。实时渲染对性能的要求极高，经常采用各种优化技巧来保证流畅度。

在实时渲染领域，渲染引擎需要对各种视觉效果进行实时计算，这包括但不限于纹理映射、光照计算、阴影、后处理效果等。

- **离线渲染（Offline Rendering）**：又称为预计算渲染或非实时渲染。这种渲染方式通常用于生成高质量的图像或动画，如电影、广告和建筑可视化。离线渲染利用物理精确的渲染算法，可产生高度逼真的视觉效果。

离线渲染通常不考虑渲染时间，因此可以使用非常复杂和计算密集型的算法来模拟光与物质的相互作用。

### 2.3 渲染引擎的关键组件

渲染引擎的实现涉及到多个核心组件。选择合适的图形API和高效利用着色器技术是构建渲染引擎的关键。

#### 2.3.1 图形API选择与使用

图形API（Application Programming Interface）是应用程序与硬件图形处理单元（GPU）之间通信的接口。选择合适的图形API至关重要，因为它会直接影响到渲染引擎的性能和跨平台能力。

- **OpenGL**：作为一种跨平台的图形API，OpenGL在桌面和移动平台上都有很好的支持。但近年来，由于驱动问题和新特性的缓慢更新，其地位逐渐被Vulkan等新API所挑战。

- **DirectX**：作为Windows平台的主要图形API，DirectX提供了对硬件更深层次的控制和优化。特别是DirectX 11和DirectX 12，前者适用于不太依赖于硬件底层的场合，而后者提供了更细粒度的资源管理以及多线程支持，适用于性能敏感型应用。

- **Vulkan**：Vulkan是近年来兴起的跨平台API，旨在提供更高效的性能和对GPU更细致的控制。它的设计目标是让开发者能够更好地利用现代硬件的并行计算能力。

选择合适的图形API后，开发者需要针对API编写特定的渲染代码，同时考虑到各个API版本的兼容性问题。

#### 2.3.2 着色器编程与高级渲染技术

着色器是运行在GPU上处理渲染数据的小程序。根据功能不同，着色器主要分为顶点着色器、片段着色器等。近年来，随着图形API的演进，还出现了计算着色器等新的类型。

- **顶点着色器（Vertex Shader）**：负责处理顶点数据，如变换、光照和法线等。顶点着色器是渲染管线中处理几何数据的第一个阶段。

- **片段着色器（Fragment Shader）**：在光栅化阶段之后执行，处理每个像素的颜色输出。它决定了最终像素的最终颜色值。

  // 简单的片段着色器示例代码
  #version 330 core
  out vec4 FragColor;
  void main() {
    FragColor = vec4(1.0f, 1.0f, 1.0f, 1.0f); // 输出白色
  }

- **高级渲染技术**：现代图形API和GPU支持诸多高级渲染技术，如实时光线追踪、全局光照（Global Illumination）、屏幕空间环境光遮蔽（SSAO）、高动态范围渲染（HDR）等。开发者可以根据需要在渲染引擎中集成和利用这些技术来增强渲染效果。

例如，在OpenGL中使用HDR技术，就需要设置浮点帧缓冲（Floating Point Framebuffer）和相关的渲染逻辑，才能实现高动态范围的显示效果。这通常涉及到复杂的数学运算和对硬件功能的深入理解。

以上为渲染引擎理论基础的详细概述。理解这些基础概念对于设计和实现一个高性能、高质量的渲染引擎至关重要。随着技术的不断演进，这些基础理论仍旧是推动图形学领域发展的核心。

# 3. C++渲染引擎核心算法

## 3.1 空间数据结构与管理

### 3.1.1 空间划分技术

空间划分技术对于渲染引擎来说至关重要，因为它直接影响到场景管理、剔除和渲染效率。空间划分技术主要分为两大类：基于图的数据结构和基于栅格的数据结构。基于图的数据结构，例如八叉树（Octree）、二叉空间分割树（BSP）等，提供了灵活的方式来表示和查询空间数据。这些结构通过递归分割空间，使得可以在对物体进行分类和查询时提供更快的检索速度。

基于栅格的数据结构如四叉树（Quadtree）和格栅（Grid）等，将空间划分为固定大小的单元格。这种结构特别适用于规则空间的管理，例如在室外大场景的渲染中，能够有效管理和查询远处的环境元素。栅格化方法的优势在于它能提供一个简单、直观的方式来处理空间数据，但是相比图结构，它在动态场景中可能会有性能上的开销。

空间数据结构的实现需要注意数据结构的选择与优化，以适应不同场景的需求。对于动态变化的环境，选择一个能够高效更新的数据结构至关重要。在C++中，可以使用指针或智能指针来管理动态创建的空间数据结构，以确保内存的正确管理。

### 3.1.2 实时剔除算法

实时剔除算法用来提高渲染效率，减少不必要的渲染计算。剔除算法如视锥剔除（Frustum Culling）、遮挡剔除（Occlusion Culling）等，是渲染引擎中不可或缺的部分。通过剔除视锥外的物体或不可见的物体，可以显著减少送往GPU处理的几何体数量，从而提升渲染性能。

视锥剔除的实现涉及到将物体包围盒与视锥体的六个平面进行相交测试。C++代码示例如下：

struct Plane {
    Vec3 normal;
    float distance;
};

bool IsBoxInFrustum( const Vec3& min, const Vec3& max, const Plane* frustumPlanes, int frustumPlaneCount ) {
    for( int i = 0; i < frustumPlaneCount; ++i ) {
        const Plane& plane = frustumPlanes[i];
        int out = 0;

        Vec3 p;
        p.x = plane.normal.x > 0.0f ? min.x : max.x;
        p.y = plane.normal.y > 0.0f ? min.y : max.y;
        p.z = plane.normal.z > 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        p.x = plane.normal.x > 0.0f ? min.x : max.x;
        p.y = plane.normal.y > 0.0f ? min.y : max.y;
        p.z = plane.normal.z < 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        p.x = plane.normal.x < 0.0f ? min.x : max.x;
        p.y = plane.normal.y > 0.0f ? min.y : max.y;
        p.z = plane.normal.z > 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        p.x = plane.normal.x < 0.0f ? min.x : max.x;
        p.y = plane.normal.y > 0.0f ? min.y : max.y;
        p.z = plane.normal.z < 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        if( out == 0 ) return true; // The box is fully within the frustum

        p.x = plane.normal.x > 0.0f ? min.x : max.x;
        p.y = plane.normal.y < 0.0f ? min.y : max.y;
        p.z = plane.normal.z > 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        p.x = plane.normal.x > 0.0f ? min.x : max.x;
        p.y = plane.normal.y < 0.0f ? min.y : max.y;
        p.z = plane.normal.z < 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        p.x = plane.normal.x < 0.0f ? min.x : max.x;
        p.y = plane.normal.y < 0.0f ? min.y : max.y;
        p.z = plane.normal.z > 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        p.x = plane.normal.x < 0.0f ? min.x : max.x;
        p.y = plane.normal.y < 0.0f ? min.y : max.y;
        p.z = plane.normal.z < 0.0f ? min.z : max.z;
        if( plane.normal.dot(p) + plane.distance < 0.0f ) out++;

        if( out == 8 ) return false; // The box is fully outside the frustum
    }

    return tru