MATLAB求不定积分：路径积分，揭开路径积分的神秘面纱

# 1. 路径积分的概念和理论基础**

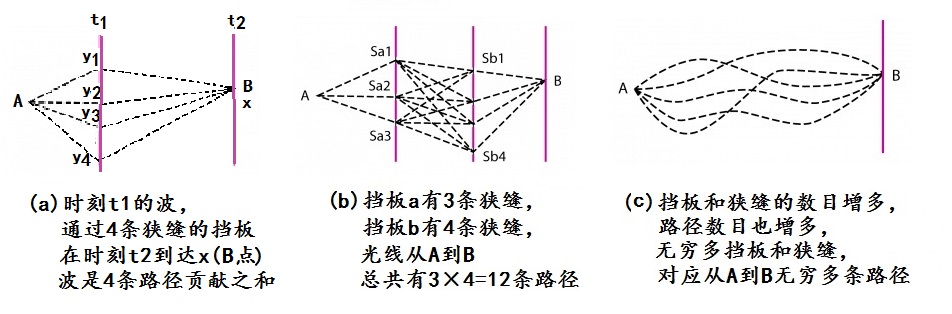
路径积分是一种数学技术，用于计算量子力学中粒子的行为。它基于这样一个概念：粒子在从一个点到另一个点移动时，会沿着所有可能的路径移动，而每个路径的概率由其作用量决定。

作用量是一个与路径相关的函数，它描述了粒子沿该路径移动所需的能量。作用量越小，粒子沿该路径移动的概率就越大。路径积分通过对所有可能路径的作用量进行求和，来计算粒子从一个点移动到另一个点的概率幅度。

概率幅度是一个复数，它包含了粒子的波函数的相位和幅度信息。通过对概率幅度的平方取模，可以得到粒子在特定位置和时间的概率密度。

# 2. 路径积分的计算方法

路径积分的计算方法主要分为数值积分方法和解析积分方法。

### 2.1 数值积分方法

数值积分方法通过将积分区间离散化，将积分近似为有限个函数值的和。常用的数值积分方法有：

#### 2.1.1 梯形法

梯形法将积分区间等分为 n 个子区间，每个子区间的面积近似为梯形的面积，积分结果为：

∫[a, b] f(x) dx ≈ (b - a) / 2 * (f(a) + f(b))

**代码块：**

% 使用梯形法计算积分
a = 0;
b = 1;
n = 100;  % 子区间个数
h = (b - a) / n;
x = linspace(a, b, n+1);
y = f(x);  % 被积函数
integral = (h / 2) * (y(1) + 2 * sum(y(2:end-1)) + y(end));

**逻辑分析：**

* `linspace(a, b, n+1)` 生成从 `a` 到 `b` 的 `n+1` 个等距点，用于计算函数值。
* `y = f(x)` 计算每个点的函数值。
* `integral` 变量存储积分结果，计算公式为梯形法公式。

#### 2.1.2 辛普森法

辛普森法比梯形法更精确，它将积分区间等分为 n 个偶数个子区间，每个子区间的面积近似为抛物线的面积，积分结果为：

∫[a, b] f(x) dx ≈ (b - a) / 6 * (f(a) + 4f((a+b)/2) + f(b))

**代码块：**

% 使用辛普森法计算积分
a = 0;
b = 1;
n = 100;  % 子区间个数
h = (b - a) / n;
x = linspace(a, b, n+1);
y = f(x);  % 被积函数
integral = (h / 6) * (y(1) + 4 * sum(y(2:2:end-2)) + 2 * sum(y(3:2:end-1)) + y(end));

**逻辑分析：**

* 与梯形法类似，生成等距点并计算函数值。
* `integral` 变量存储积分结果，计算公式为辛普森法公式。

#### 2.1.3 龙贝格积分

龙贝格积分是一种自适应积分方法，它将积分区间递归地细分为子区间，直到满足预定的精度要求，积分结果为：

∫[a, b] f(x) dx ≈ ∫[a, c] f(x) dx + ∫[c, b] f(x) dx

**代码块：**

% 使用龙贝格积分计算积分
a = 0;
b = 1;
tol = 1e-6;  % 容差
max_depth = 10;  % 最大递归深度
integral = romberg(f, a, b, tol, max_depth);

**逻辑分析：**

* `romberg` 函数实现龙贝格积分算法。
* `tol` 参数指定容差，当积分结果的绝对误差小于 `tol` 时，算法停止。
* `max_depth` 参数指定最大递归深度，防止算法陷入无限递归。

### 2.2 解析积分方法

解析积分方法利用积分公式和微积分技术直接求解积分。常用的解析积分方法有：

#### 2.2.1 复变积分

复变积分将实积分转化为复平面的积分，利用复分析中的定理和公式进行求解。

**代码块：**

% 使用复变积分计算积分
f = @(z) 1 / (z^2 + 1);
a = 0;
b = 1;
integral = integral(@(t) f(a + (b-a)*t), 0, 1);