Java排序算法的扩展探索：计数排序、基数排序的非比较排序方法

# 1. 排序算法基础

排序算法是计算机科学中的基础算法之一，它涉及到将一组数据按照一定的顺序进行排列。本章节将为读者提供排序算法的概览，从而为后续章节中更高级的排序算法，例如计数排序和基数排序的学习打下坚实的基础。

## 1.1 排序算法的重要性

排序算法在日常开发中极为常见，无论是数据库索引的创建、搜索引擎结果的排序还是数据可视化中数据的组织，都需要使用排序算法。正确的排序方法能够显著提升数据处理的效率和准确性。

## 1.2 基本排序算法简介

排序算法根据其操作方式可以分为两大类：比较排序和非比较排序。比较排序通过比较元素间的大小来决定元素的排列顺序，而非比较排序则利用数据中的其他信息来进行排序。常见的比较排序算法包括冒泡排序、选择排序、插入排序、归并排序、快速排序等；而非比较排序则包括计数排序、基数排序和桶排序等。在下一章节，我们将详细介绍计数排序的原理和实践。

## 1.3 排序算法的性能比较

不同的排序算法在时间复杂度、空间复杂度和稳定性方面各有优劣。例如，快速排序具有较好的平均时间复杂度O(n log n)，但最坏情况下的时间复杂度会退化到O(n^2)。而计数排序则可以在特定情况下达到线性时间复杂度O(n+k)，但其对输入数据的范围有限制。理解这些基础概念对于选择合适的排序算法至关重要。

# 2. 计数排序的理论与实践

### 2.1 计数排序的基本原理

#### 2.1.1 排序算法的分类
在介绍计数排序之前，我们先来了解一下排序算法的分类。排序算法可以分为两类：比较型排序和非比较型排序。比较型排序算法的典型代表有快速排序、归并排序等，它们利用比较操作将元素进行顺序排列。而非比较型排序算法，如计数排序、基数排序和桶排序，它们不直接比较两个元素的大小，而是利用数据的特性来进行排序。

计数排序是一种非比较型的排序算法，它适用于一定范围内的整数排序。与比较排序算法不同的是，计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。

#### 2.1.2 计数排序的工作机制
计数排序的工作机制可以概括为以下几个步骤：
1. 找出待排序的数组中的最大值和最小值。
2. 计算待排序数组的最大值与最小值之差，设为范围K。
3. 创建一个计数数组C，大小为K+1，初始时所有值为0。
4. 遍历待排序数组，统计每个值的出现次数并记录到计数数组C中。
5. 根据计数数组C计算每个元素在最终排序数组中的位置。
6. 根据计算出的位置，将原数组中的元素放到最终的位置上。

这种算法特别适用于当输入的元素是小范围整数时，它能够利用计数数组对原数组的元素进行重排，从而达到排序的目的。

### 2.2 计数排序的实现细节

#### 2.2.1 算法的流程图

graph TD
A[开始] --> B[找到数组中的最大最小值]
B --> C[计算最大最小值之差]
C --> D[创建计数数组]
D --> E[遍历原数组，计数]
E --> F[计算元素位置]
F --> G[按照位置重排原数组]
G --> H[结束]

#### 2.2.2 时间和空间复杂度分析
计数排序的时间复杂度为O(n+k)，其中n为待排序数组的长度，k为待排序数组中最大数和最小数的差值。空间复杂度为O(k)，这是因为需要额外的计数数组来记录元素出现的次数。由于计数排序不是比较排序，它不受O(nlogn)下界的影响，因此对于小范围整数排序来说，计数排序的效率是非常高的。

### 2.3 计数排序的实际应用场景

#### 2.3.1 数据分布特性分析
计数排序最理想的应用场景是输入数据范围有限且分布均匀。例如，在处理一个班级学生考试成绩的排序问题时，如果学生的分数范围在0到100之间，那么可以使用计数排序。因为学生的分数范围是固定的，且容易计算出最大值和最小值之差，创建计数数组的大小会很小，排序效率很高。

#### 2.3.2 代码示例与性能测试
以下是使用Python实现的计数排序的代码示例：

def counting_sort(arr):
    if not arr:
        return []

    # 找到最大值和最小值
    max_val = max(arr)
    min_val = min(arr)
    range_val = max_val - min_val + 1
    # 创建计数数组并初始化为0
    counter_arr = [0] * range_val
    # 计算每个元素出现的次数
    for num in arr:
        counter_arr[num - min_val] += 1
    # 根据计数数组重排原数组
    index = 0
    for num in range(len(counter_arr)):
        while counter_arr[num] > 0:
            arr[index] = num + min_val
            index += 1
            counter_arr[num] -= 1
    return arr

# 性能测试
import random
import time

test_array = [random.randint(0, 100) for _ in range(1000)]
start = time.time()
counting_sort(test_array)
end = time.time()
print(f"Counting Sort took {end - start} seconds.")

在这个代码示例中，我们首先定义了一个`counting_sort`函数来执行计数排序。接着，我们用随机生成的包含1000个0到100之间整数的数组进行测试，并计算排序所用的时间。

计数排序在处理像上述这种范围不大、分布均匀的整数数组时，通常会有非常好的性能表现。然而，如果数据分布不均匀，或者数据范围非常大，计数排序的效率就会下降。在实际应用中，应当根据数据的具体特点选择合适的排序方法。

# 3. 基数排序的理论与实践

## 3.1 基数排序的基本原理
### 3.1.1 排序算法的分类
排序算法可以按照不同的标准进行分类，其中一种主要的分类是比较型排序和非比较型排序。比较型排序（例如快速排序、归并排序）主要通过元素之间的比较来进行排序，而非比较型排序（例如计数排序、基数排序）则不直接进行元素之间的比较。在所有排序算法中，非比较型排序算法通常在特定条件下具有更优的性能表现，特别是在处理大数据集和整数数据时。基数排序就是一种典型的非比较型排序算法。

### 3.1.2 基数排序的工作机制
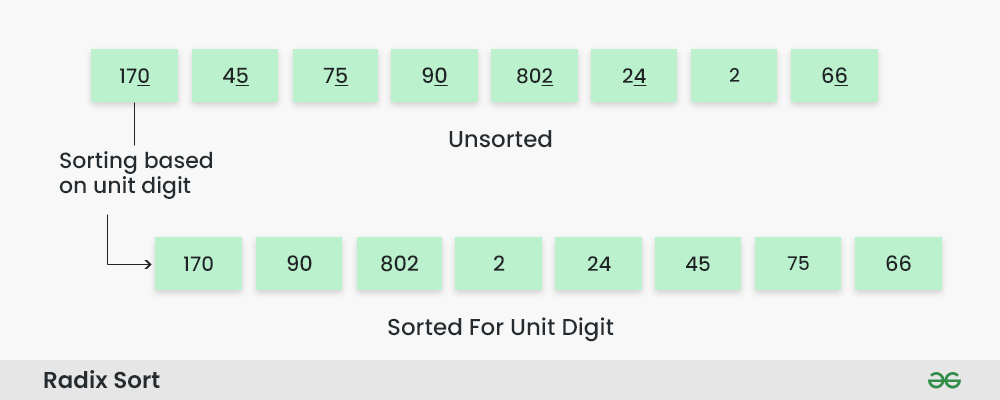
基数排序是一种按照“位权”（即位置的权重）来分配、收集数据，以达到排序目的的算法。它将整数按位数切割成不同的数字，然后按每个位数分别比较。在比较每一位时，根据该位数的值将数据分配到相应的桶（bucket）中。对每一位执行完排序后，再根据下一个更低的位进行同样的处理，以此类推，直到最低位处理完毕。

基数排序通常使用"最右优先"（Least S