Java排序算法内部揭秘：分析不同算法的工作原理

# 1. Java排序算法概述

在计算机科学和编程领域中，排序算法扮演着至关重要的角色。排序不仅是数据处理和分析的基石，而且在优化算法性能和资源使用方面具有深远意义。Java作为一种广泛使用的编程语言，提供了多种排序工具和方法。在深入分析具体排序算法之前，本章将概述排序算法的基本概念，包括其分类、应用场景以及在Java中的实现基础。我们将从基本的排序需求出发，逐步探索Java排序算法的多样性和复杂性，为理解后续章节中的具体算法奠定坚实的基础。

# 2. 基本排序算法解析

## 2.1 简单排序算法

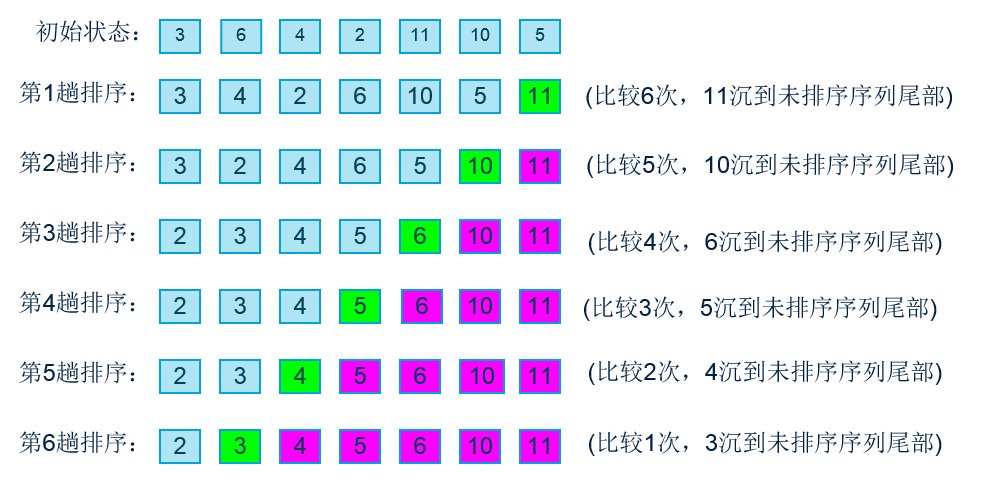
### 2.1.1 冒泡排序：从头到尾的交换过程

冒泡排序是一种简单的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

这个算法的名字由来是因为越小（或越大）的元素会经由交换慢慢“浮”到数列的顶端。

以下是冒泡排序的Java实现示例：

public class BubbleSort {
    public void bubbleSort(int arr[]) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    // 交换 arr[j+1] 和 arr[j]
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }
}

冒泡排序算法的性能分析：

- 最佳情况：T(n) = O(n)，当输入的数据已经是正序时（假设从小到大排序）。
- 最差情况：T(n) = O(n^2)，当输入的数据是反序时。
- 平均情况：T(n) = O(n^2)，因为每一轮的比较都需要进行交换操作，所以时间复杂度较高。

### 2.1.2 选择排序：寻找最小（大）元素的过程

选择排序算法是一种原址比较排序算法。选择排序大致的思路是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

选择排序是不稳定的排序方法，它不像冒泡排序那样可以较为容易地进行优化。在Java中实现选择排序算法的代码如下：

public class SelectionSort {
    public void selectionSort(int arr[]) {
        int n = arr.length;

        for (int i = 0; i < n - 1; i++) {
            // 找到最小元素的索引
            int min_idx = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[min_idx]) {
                    min_idx = j;
                }
            }

            // 将找到的最小元素与i位置所在元素交换
            int temp = arr[min_idx];
            arr[min_idx] = arr[i];
            arr[i] = temp;
        }
    }
}

选择排序算法的性能分析：

- 最佳情况、最差情况和平均情况下的时间复杂度均为O(n^2)。

### 2.1.3 插入排序：插入元素的有序化

插入排序的工作方式像很多人在打扑克牌时整理牌一样。在扑克牌中，如果牌是随机的，那么我们会按照一定的顺序（大小或者花色）将其排序。我们从牌堆里拿出一张牌，并将其插入到已经排好序的一堆牌中的适当位置。

插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

以下是插入排序的Java实现示例：

public class InsertionSort {
    public void insertionSort(int arr[]) {
        int n = arr.length;
        for (int i = 1; i < n; ++i) {
            int key = arr[i];
            int j = i - 1;

            // 将arr[i]移动到其在前面已排序序列的正确位置
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j = j - 1;
            }
            arr[j + 1] = key;
        }
    }
}

插入排序算法的性能分析：

- 最佳情况：T(n) = O(n)，当输入数据已经是正序时。
- 最差情况：T(n) = O(n^2)，当输入数据是反序时。
- 平均情况：T(n) = O(n^2)。

## 2.2 分而治之的排序算法

### 2.2.1 归并排序：分解-合并的过程

归并排序是一种分而治之的算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

具体来说，归并排序算法包含两个基本操作：

1. 分割：递归地把当前序列平均分割成两半。
2. 合并：合并两个排序好的子序列。

Java中归并排序的一个简单实现如下：

public class MergeSort {
    void merge(int arr[], int l, int m, int r) {
        int i, j, k;
        int n1 = m - l + 1;
        int n2 = r - m;

        // 创建临时数组
        int L[] = new int[n1];
        int R[] = new int[n2];

        // 拷贝数据到临时数组
        for (i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];

        // 合并临时数组回 arr[l..r]
        i = 0; // 初始化第一个子数组的索引
        j = 0; // 初始化第二个子数组的索引
        k = l; // 初始归并子数组的索引
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        // 拷贝 L[] 的剩余元素
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }

        // 拷贝 R[] 的剩余元素
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    void sort(int arr[], int l, int r) {
        if (l < r) {
            // 找到中间索引
            int m = l + (r - l) / 2;

            // 分别递归排序两半
            sort(arr, l, m);
            sort(arr, m + 1, r);

            // 合并排序好的两半
            merge(arr, l, m, r);
        }
    }
}

归并排序算法的性能分析：

- 最佳、最差和平均情况下的时间复杂度均为O(nlogn)，因为它每次都是将序列分割成两半来处理。

### 2.2.2 快速排序：分区-递归的过程

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要 O(nlogn) 次比较。在最坏状况下则需要 O(n^2) 次比较，但这种状况并不常见。

快速排序使用分治法（Divide and Conquer）策略来把一个序列分为较小和较大的两个子序列，然后递归地排序两个子序列。

快速排序的一个简单实现如下：

public class QuickSort {
    int partition(int arr[], int low, int high) {
        int pivot = arr[high];
        int i = (low - 1);

        for (int j = low; j < high; j++) {
            if (arr[j] < pivot) {
                i++;

                // 交换 arr[i] 和 arr[j]
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }

        // 交换 arr[i+1] 和 arr[high] (或 pivot)
        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;

        return i + 1;
    }

    void quickSort(int arr[], int low, int high) {
        if (low < high) {
            // pi 是分区索引，arr[pi] 现在在正确的位置
            int pi = partition(arr, low, high);

            // 分别递归地排序子序列
            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }
}

快速排序算法的性能分析：

- 最佳情况：T(n) = O(nlogn)，当输入数据已有序时。
- 最差情况：T(n) = O(n^2)，当输入数据全部相同，或者每次选择的基准都是最小或最大值时。
- 平均情况：T(n) = O(nlogn)。

### 2.2.3 堆排序：构建堆与排序的结合

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

在堆数据结构中，堆中的最大元素总是位于根节点，堆排序就是利用这个特性实现的。

堆排序的Java实现示例如下：

public class HeapSort {
    public void sort(int arr[]) {
        int n = arr.length;

        // 构建最大堆
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }

        // 一个个从堆顶取出元素
        for (int i = n - 1; i >= 0; i--) {
            // 移动当前根到数组的末尾
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            // 调用 max heapify 在减小的堆上
            heapify(arr, i, 0);
        }
    }

    // 以 i 为根的子树进行调整
    void heapify(int arr[], int n, int i) {
        int largest = i;
        int l = 2 * i