Java排序算法面试必备：解答面试官的5大常见问题

# 1. Java排序算法基础

排序是计算机科学中的基础概念，对于任何需要对数据进行组织的程序来说都是必不可少的。在Java中，排序算法是学习数据结构和算法的起点，其重要性不言而喻。本章将概述Java中排序算法的基本原理和分类，为深入理解后续更复杂的排序算法奠定坚实的基础。

## 1.1 排序算法的重要性

排序算法能够将一组无序的数据转换为有序的状态，是编程中常见的任务之一。在Java中，排序不仅限于简单的数组或列表元素，还包括对象集合的排序，甚至可以用于文件或数据库查询结果的排序。掌握排序算法，能够提高程序的运行效率，优化用户体验。

## 1.2 排序算法的基本概念

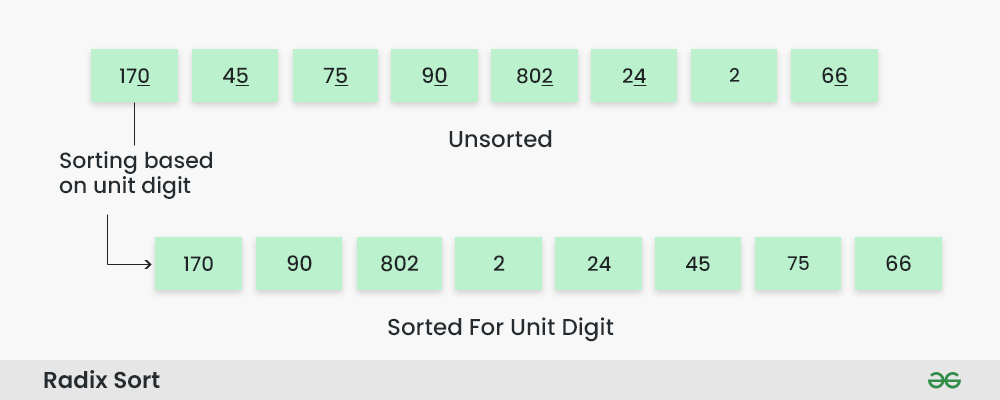
在进一步了解排序算法之前，有必要先了解一些基本概念。排序算法主要可以分为两种：比较排序和非比较排序。比较排序是指通过比较元素之间的大小关系来决定它们的顺序，而非比较排序则不依赖于元素间的比较，例如计数排序和基数排序。此外，排序算法的性能通常通过时间复杂度和空间复杂度来衡量，这些概念将在后续章节中详细解释。

## 1.3 排序算法的分类

Java排序算法可以按照不同的维度进行分类。根据算法操作的稳定性，排序算法可以分为稳定排序和非稳定排序；根据算法的适用场景和性能特点，又可以分为内部排序和外部排序。本章会为读者展示如何基于Java特性来选择和实现各种基础排序算法，为后续高级排序技巧的学习打下坚实的基础。

通过以上内容，读者应该能够对Java排序算法有初步的认识，并期待在后续章节中学习到更深入的排序算法知识。

# 2. 经典排序算法详解

## 2.1 冒泡排序算法

### 2.1.1 冒泡排序的基本原理

冒泡排序是一种简单的排序算法。它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

该算法的平均时间复杂度和最坏情况下的时间复杂度均为 O(n^2)，其中 n 是数组的长度。由于其算法复杂度较高，冒泡排序一般只适用于小规模数据集的排序。

### 2.1.2 实现冒泡排序的代码

以下是使用 Java 实现冒泡排序的一个基本示例：

public void bubbleSort(int[] arr) {
    if (arr == null || arr.length == 0)
        return;
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                // 交换 arr[j] 和 arr[j+1]
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

### 2.2 快速排序算法

#### 2.2.1 快速排序的工作机制

快速排序（Quick Sort）使用了分治法（Divide and Conquer）的策略。它首先选择一个元素作为基准（Pivot），通常选择数组中间的元素。然后，将数组中小于基准的元素放在基准前面，大于基准的元素放在基准后面。这个过程称为分区（Partitioning）。递归地（recursive）在基准的左右两边执行同样的操作，直到所有的元素都排序好。

快速排序的平均时间复杂度为 O(n log n)，在最好的情况下可以达到 O(n log n)，最坏情况会退化到 O(n^2)，但这种情况较为罕见。快速排序由于其优秀的平均性能，在实际应用中被广泛使用。

#### 2.2.2 快速排序的代码实现

以下是一个快速排序算法的 Java 实现示例：

public void quickSort(int[] arr, int low, int high) {
    if (arr == null || arr.length == 0)
        return;
    if (low >= high)
        return;
    // 选择中间值作为基准
    int middle = low + (high - low) / 2;
    int pivot = arr[middle];
    // 分区操作
    int i = low, j = high;
    while (i <= j) {
        while (arr[i] < pivot) {
            i++;
        }
        while (arr[j] > pivot) {
            j--;
        }
        if (i <= j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++;
            j--;
        }
    }
    // 递归调用
    if (low < j)
        quickSort(arr, low, j);
    if (high > i)
        quickSort(arr, i, high);
}

### 2.3 归并排序算法

#### 2.3.1 归并排序的理论基础

归并排序是一种分治算法，其思想是将数组分成两部分，分别进行排序，然后将排序好的两部分合并在一起，合并时也按顺序合并，最后得到完全有序的数组。由于归并排序的合并操作需要与数组等长的额外空间，因此它的空间复杂度为 O(n)。

归并排序算法的时间复杂度稳定在 O(n log n)，因此它也是一种效率较高的排序算法。特别适合对大数据量进行排序。

#### 2.3.2 归并排序的步骤详解

1. **分解**：不断地将数组分成两半进行分割，直到每个子数组只有一个元素或为空。
2. **合并**：将两个有序的子数组合并成一个有序的数组。
3. **重复**：递归地重复步骤1和2直到整个数组排序完成。

以下是归并排序的 Java 实现：

public void mergeSort(int[] arr, int[] temp, int leftStart, int rightEnd) {
    if (leftStart >= rightEnd)
        return;
    int middle = (leftStart + rightEnd) / 2;
    mergeSort(arr, temp, leftStart, middle);
    mergeSort(arr, temp, middle + 1, rightEnd);
    mergeHalves(arr, temp, leftStart, rightEnd);
}

private void mergeHalves(int[] arr, int[] temp, int leftStart, int rightEnd) {
    int leftEnd = (rightEnd + leftStart) / 2;
    int rightStart = leftEnd + 1;
    int size = rightEnd - leftStart + 1;
    int left = leftStart;
    int right = rightStart;
    int index = leftStart;
    while (left <= leftEnd && right <= rightEnd) {
        if (arr[left] <= arr[right]) {
            temp[index] = arr[left];
            left++;
        } else {
            temp[index] = arr[right];
            right++;
        }
        index++;
    }
    System.arraycopy(arr, left, temp, index, leftEnd - left + 1);
    System.arraycopy(arr, right, temp, index, rightEnd - right + 1);
    System.arraycopy(temp, leftStart, arr, leftStart, size);
}

### 2.4 堆排序算法

#### 2.4.1 堆排序的堆结构介绍

堆排序（Heap Sort）是利用堆这种数据结构所设计的一种排序算法。堆是一种近似完全二叉树的结构，并同时满足堆积的性质，即子节点的键值或索引总是小于（或者大于）它的父节点。

在堆结构中，有以下两种重要的堆类型：

- 最大堆（Max Heap）：任何一个父节点的值，都大于或等于它的孩子节点。
- 最小堆（Min Heap）：任何一个父节点的值，都小于或等于它的孩子节点。

堆排序算法就是利用这个性质来进行排序的。

#### 2.4.2 堆排序的实现方法

堆排序算法主要分为两个步骤：

1. **建堆**：将输入的无序数组调整为最大堆。
2. **排序**：依次将最大堆的根节点（数组的第一个元素）与堆的最后一个元素交换，然后将剩下的元素重新调整为最大堆，重复这个过程直到数组有序。

以下是堆排