图算法中的递归探索：深度解析递归在最短路径与拓扑排序中的应用

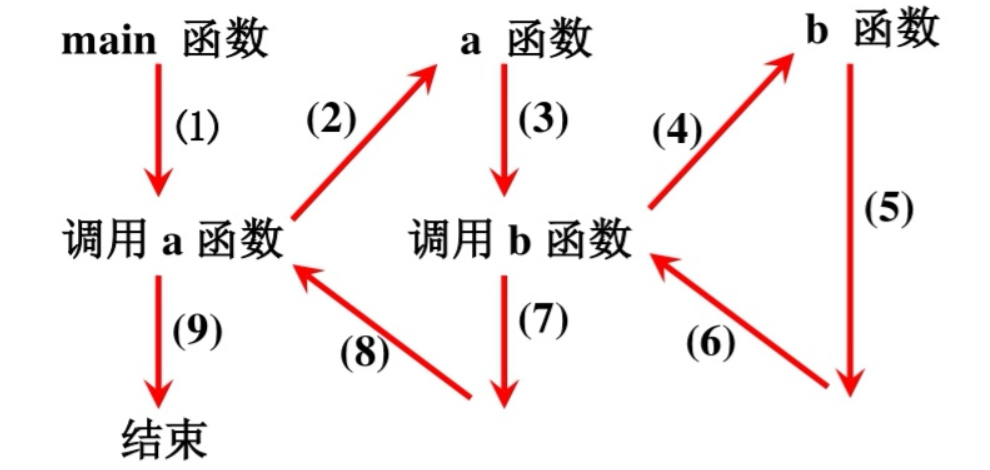
# 1. 图算法与递归的基本概念

在探索图算法的世界之前，我们必须首先建立对图论和递归的初步理解。图是一种抽象的数据结构，它由一系列节点（也称为顶点）和这些节点之间的连接（称为边）组成。图算法广泛应用于计算机科学和数据分析领域，如社交网络分析、物流运输、搜索引擎优化等。递归是一种编程技巧，其中函数直接或间接地调用自身来解决问题。在图算法中，递归通常用于遍历和搜索图结构，以及求解复杂问题。本章我们将讨论图算法和递归的基本概念，为进一步深入研究打下坚实的基础。

## 1.1 图的表示方法
图可以用多种方式表示，常见的有邻接矩阵和邻接表。邻接矩阵是一个二维数组，每个元素表示两个顶点之间的连接状态。邻接表则是一组链表，每个链表包含与特定顶点相连的所有顶点。例如，在Python中，可以使用字典来实现邻接表：

graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

## 1.2 递归的基本原理
递归函数通过反复调用自身来解决问题，直到达到一个简单的基本情形。递归函数需要两个主要部分：基本情况（递归终止条件）和递归步骤（函数调用自身的步骤）。例如，计算阶乘的递归函数：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

通过本章的内容，读者将对图算法和递归有一个基础的了解，为深入研究图算法中的递归应用奠定基础。

# 2. 递归在图的最短路径问题中的应用

在第二章中，我们将深入探讨递归算法在图的最短路径问题中的应用。我们将从最短路径问题的基本概念讲起，接着分析递归算法如何实现最短路径的查找，最后通过实际应用场景来理解递归在解决实际问题中的作用和效率。

## 2.1 最短路径问题概述

### 2.1.1 最短路径问题定义
最短路径问题是图论中的一个经典问题，它要求在图中找到从一个顶点到另一个顶点的最短路径，这个路径上的总权重是最小的。在实际应用中，最短路径问题广泛应用于网络路由、地图导航、社交网络分析等领域。

### 2.1.2 常见最短路径算法简介
为了更好地理解递归在最短路径问题中的应用，首先简要介绍几种常见的最短路径算法：
- Dijkstra算法：适用于带有非负权重的图，通过贪心策略找到最短路径。
- A*算法：加入了启发式搜索，适用于带有启发信息的图。
- Floyd-Warshall算法：可以同时计算图中所有顶点对的最短路径。
- Bellman-Ford算法：能够处理带有负权重的图，但不能有负权重环。

## 2.2 递归算法实现最短路径

### 2.2.1 Dijkstra算法的递归版本
Dijkstra算法通常使用贪心策略和优先队列实现，但是它也可以用递归方式实现。下面将展示递归版本的Dijkstra算法如何在代码层面上解决问题。

import heapq

def dijkstra_recursive(graph, start, visited=None, distances=None):
    if visited is None:
        visited = set()
    if distances is None:
        distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0

    # 使用优先队列来优化递归查找过程
    priority_queue = [(0, start)]
    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)

        if current_vertex in visited:
            continue

        visited.add(current_vertex)

        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances

在上述代码中，我们使用了递归函数`dijkstra_recursive`来计算从`start`顶点到图中所有其他顶点的最短路径。我们使用一个最小堆来保持优先队列，以确保每次都能访问到当前距离最小的顶点。递归的核心在于不断尝试从未访问的顶点中找到最近的顶点，并更新到其他顶点的距离。

### 2.2.2 Bellman-Ford算法与递归
尽管Bellman-Ford算法的主要实现不基于递归，我们可以通过引入递归来处理特定情况，例如在不含有负权重环的图中找到最短路径。递归版本的Bellman-Ford算法可以用来探索递归在动态规划问题中的应用。

## 2.3 最短路径问题的递归实践

### 2.3.1 实际应用场景举例
在实际应用场景中，递归算法可以解决一些复杂的最短路径问题。例如，在网络路由中，递归可以用来更新路由表，而递归的深度可以帮助处理网络的层次结构。

### 2.3.2 代码实现与效率分析
在具体的代码实现中，递归算法通常伴随着较高的空间复杂度，因为它需要保存每一层递归调用的状态。效率分析包括时间复杂度和空间复杂度，以及它们如何受到问题规模的影响。

例如，如果使用递归实现Dijkstra算法，其时间复杂度仍为O((V+E)logV)，但空间复杂度将增加，因为每个递归调用都会创建新的状态。这种额外的空间开销可能会成为效率问题，特别