递归思维训练营：7大经典问题解锁递归解题策略

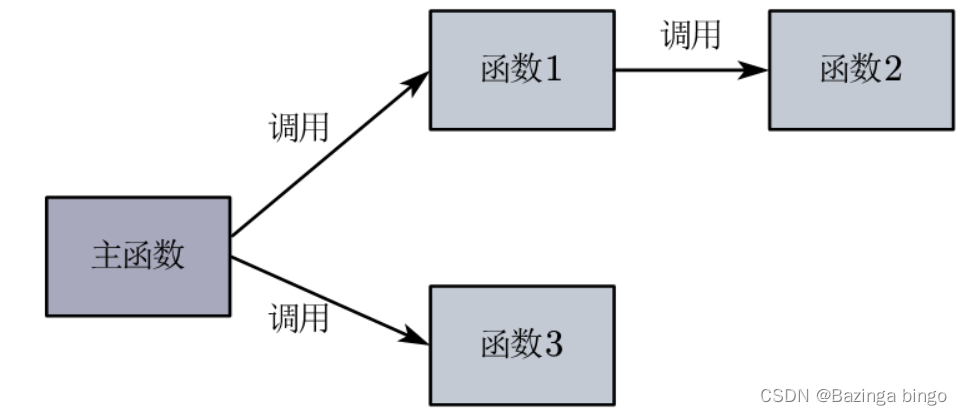
# 1. 递归思维的数学原理与哲学

## 1.1 递归的定义与本质

递归是计算机科学和数学中的一种常见概念，指的是一个过程或函数直接或间接地调用自身以解决问题。在数学领域，递归关系可以追溯到古希腊时期，而其哲学意义则源自对无限和自我相似性的思考。从本质上讲，递归提供了一种描述问题和解决问题的方式，尤其是在处理分形结构和自然迭代过程中。

## 1.2 递归与数学归纳法

递归与数学归纳法有着密切的联系。通过建立一个数学命题关于自然数的递归关系，并且证明最小情况（基础案例）成立，然后假设对于某个自然数k的情况成立，接着推导出k+1的情况也成立，从而证明整个命题。这种方法不仅在数学证明中广泛使用，同样适用于计算机程序设计中的递归算法。

## 1.3 递归思维的哲学内涵

递归思维不仅仅是一种解决问题的技术手段，它还体现了复杂系统中自相似和自组织的原则。在哲学上，递归可以被看作是理解世界的一种模式，强调了局部与整体的关系，以及在各种层面上相似性的出现。递归思维启示我们，通过分析局部结构和规则，可以解释和预测整体行为。

# 2. 递归算法的基本结构与应用

## 2.1 递归算法的构成要素

递归算法是程序设计中一种重要的逻辑思维方法，它的核心在于函数自我调用。理解递归算法的构成要素对于掌握递归思想至关重要。

### 2.1.1 基本案例（Base Case）

在递归算法中，基本案例是递归结束的条件。它是一组特定的输入，使得问题可以不经过进一步的递归调用而直接解决。

def factorial(n):
    if n == 0:  # 基本案例
        return 1
    else:
        return n * factorial(n - 1)

在上述的阶乘函数中，`n == 0` 是基本案例。当函数递归调用自己时，如果输入的 `n` 为 0，那么它不再进行递归调用，而是直接返回结果 1。

### 2.1.2 递归步骤（Recursive Step）

递归步骤是递归函数中定义如何将问题分解为更小问题的部分。这通常通过函数调用自身实现，每次调用都使问题规模缩小。

def sum_of_elements(arr, n):
    if n <= 0:  # 基本案例
        return 0
    else:
        return arr[n-1] + sum_of_elements(arr, n-1)  # 递归步骤

在上面的求和函数中，递归步骤是 `arr[n-1] + sum_of_elements(arr, n-1)`，其中 `arr[n-1]` 是当前数组元素，`sum_of_elements(arr, n-1)` 是对数组的前 `n-1` 个元素进行求和的递归调用。

## 2.2 递归与迭代的比较

递归和迭代是解决问题的两种常见方法，它们在不同的场景下具有各自的优势和局限性。

### 2.2.1 递归的优势与局限

递归的优势主要体现在代码的简洁性和直观性。特别是对于树形或分形结构的问题，递归能够直观地反映问题的结构。

然而，递归也有其局限性。例如，在某些编程语言中，递归过深可能导致栈溢出错误。此外，递归的性能通常不如迭代，因为它需要额外的函数调用开销。

### 2.2.2 迭代的优势与局限

迭代的优势在于效率较高，尤其是在处理大规模数据时，可以避免递归调用的栈空间开销。

然而，迭代的局限在于有时代码的可读性和简洁性不如递归。特别是对于复杂的问题，迭代版本的代码可能难以理解。

## 2.3 递归算法的性能分析

递归算法的性能分析对于预测和优化程序的执行非常重要。

### 2.3.1 时间复杂度分析

递归算法的时间复杂度分析通常基于递归树的概念，分析递归过程中子问题的数量和每个子问题的计算量。

### 2.3.2 空间复杂度分析

空间复杂度分析关注的是递归算法在运行过程中需要消耗多少内存空间，主要分析的是函数调用栈的大小。

表格形式展示时间复杂度和空间复杂度的例子：

| 算法 | 时间复杂度 | 空间复杂度 |
|------|------------|------------|
| 斐波那契递归 | O(2^n) | O(n) |
| 斐波那契迭代 | O(n) | O(1) |
| 快速排序 | O(n log n) | O(log n) |

代码块展示递归算法的空间复杂度分析：

def recursive_sum(arr, n):
    if n <= 0:
        return 0
    else:
        return arr[n-1] + recursive_sum(arr, n-1)

# 计算递归调用栈深度
stack_depth = 0
def check_stack_depth(n):
    global stack_depth
    stack_depth += 1
    if n > 0:
        check_stack_depth(n - 1)
    stack_depth -= 1

check_stack_depth(len(arr))
print(f"Space complexity is O({stack_depth})")

递归算法的性能分析不仅仅是计算复杂度，还包括对递归调用栈的理解和测试，因为递归深度过大可能会导致栈溢出。

# 3. ```
# 第三章：7大经典问题的递归解析

递归作为一种编程技巧，能够将复杂问题简化为更小的子问题。它在解决经典问题方面有着独特的优势。接下来，我们将探讨七个利用递归方法可以有效解决的经典问题，不仅会分析递归实现的过程，也会探讨性能优化方法以及递归与其他方法的对比。

## 3.1 斐波那契数列问题

斐波那契数列是一个典型的递归问题，广泛应用于算法学习和实际编程中。它由以下递归关系定义：F(0)=0, F(1)=1, 对于 n>1, F(n)=F(n-1)+F(n-2)。

### 3.1.1 数列定义与递归实现

递归实现斐波那契数列问题非常直观，代码如下：

def fibonacci(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

#### 参数说明与执行逻辑

- `n`：期望计算的斐波那契数列中的位置。
- `if n <= 0`：处理负数或零的特殊情况。
- `elif n == 1`：处理基本情况，即数列中的第一个数。
- `else`：递归调用自身来计算前两个斐波那契数，并返回它们的和。

#### 性能分析

虽然这段代码直观且易于理解，但是它的时间复杂度为 O(2^n)，因为树形递归结构造成了大量的重复计算。为了提高性能，通常会使用动态规划技术来避免重复计算，从而达到 O(n) 的时间复杂度。

### 3.1.2 优化递归性能的方法

在斐波那契数列问题中，我们可以使用“记忆化”来优化递归过程中的性能问题。记忆化是将已经计算过的结果存储起来，以避免重复计算。

def fibonacci_memo(n, memo={}):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    if n not in memo:
        memo[n