【Boosting算法演变全解析】：从AdaBoost到XGBoost的深度探索

# 1. Boosting算法的概念和起源

## 1.1 Boosting的定义
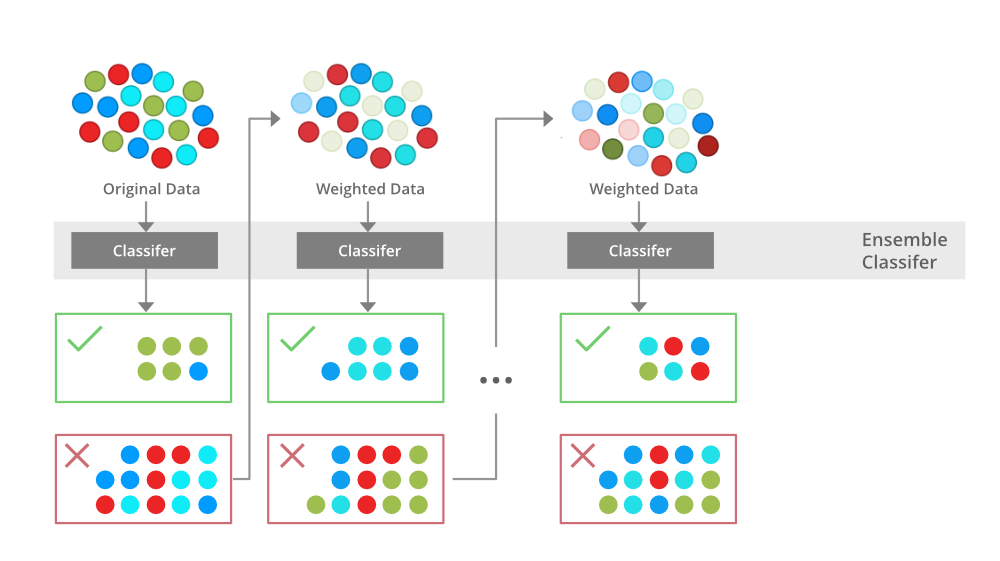
Boosting是一类可将弱学习器提升为强学习器的算法。在机器学习领域中，它通过组合多个模型来改善整体的性能。这一过程相当于投票，每个模型对最终结果都有一定的贡献。

## 1.2 历史与演变
Boosting最初由Robert Schapire于1990年提出，后来Freund和Schapire对其进行了改进，提出了Adaptive Boosting（AdaBoost），极大推动了 Boosting 算法的发展。后续的研究工作衍生出更多高效的Boosting变体，如Gradient Boosting和XGBoost。

## 1.3 应用前景
Boosting算法由于其出色的泛化能力和适应性，在数据挖掘、计算机视觉、自然语言处理等众多领域都有广泛的应用前景。通过组合多个模型，Boosting能够处理更为复杂的数据模式，提供更加精确的预测。

Boosting算法家族通过不断的发展与优化，现已成为机器学习领域中不可或缺的工具之一。接下来的章节将详细讨论该算法家族中的重要成员，包括它们的原理、实现方法以及实际应用场景。

# 2. AdaBoost算法原理与实现

### 2.1 AdaBoost的核心概念

#### 2.1.1 弱学习器和强学习器

在AdaBoost中，"弱学习器"指的是一个分类器，它仅比随机猜测好一点，其性能微弱，比如单层决策树或感知器。"强学习器"则相反，它具有较高准确性，如深度决策树、SVM、神经网络等。AdaBoost的目标就是通过组合这些弱学习器，构建出一个强学习器。

实现弱学习器的一个简单示例可以是随机选择一个特征，然后根据该特征的值是否超过一个阈值来进行分类决策。

import numpy as np

def weak_learner(data, labels):
    # 选择随机特征进行分割
    random_feature = np.random.randint(0, data.shape[1])
    unique, counts = np.unique(data[:, random_feature], return_counts=True)
    threshold = unique[np.argmin(counts)]  # 最少的点的阈值
    # 分割决策
    predictions = (data[:, random_feature] > threshold).astype(int)
    return predictions

#### 2.1.2 权重更新机制

权重更新是AdaBoost的核心部分。每个样本被赋予一个权重，初始时所有权重相等。每次错误分类的样本权重会增加，而正确分类的样本权重会减少。这样，弱学习器接下来就会更加关注那些之前被错误分类的样本。

def update_weights(errors, weights, total):
    beta = np.sum(errors * weights) / np.sum(errors)
    new_weights = np.multiply(weights, np.exp(-errors * labels * np.log(1 - beta) / np.log(1 - 0.5)))
    new_weights = new_weights / np.sum(new_weights) * total
    return new_weights, beta

### 2.2 AdaBoost的数学模型

#### 2.2.1 损失函数的定义

在AdaBoost中，损失函数是指数损失，它是模型预测错误的惩罚函数。指数损失随着预测值与真实值偏离程度的增加而指数级增长。

def exponential_loss(labels, predictions):
    return np.mean(np.exp(-labels * predictions))

#### 2.2.2 模型组合策略

模型的组合策略是指如何将多个弱学习器的预测结果汇总成一个最终的预测结果。在AdaBoost中，通过赋予每个弱学习器一个权重，并将这些加权预测结果相加来得到最终的强学习器输出。

def combine_predictions(predictions_list, weights):
    return np.array([np.sign(np.sum(w * p)) for p, w in zip(predictions_list, weights)])

### 2.3 AdaBoost的应用实践

#### 2.3.1 算法的实际编码实现

为了实现一个完整的AdaBoost算法，我们需要编写代码来迭代地训练弱学习器，并更新样本权重。

def adaboost_train(data, labels, num_classifier):
    # 初始化样本权重
    weights = np.full(len(labels), 1 / len(labels))
    predictions_list = []
    weights_list = []
    for _ in range(num_classifier):
        predictions = weak_learner(data, labels)
        errors = np.abs(predictions - labels) / 2  # 0或0.5
        weights, beta = update_weights(errors, weights, len(labels))
        predictions_list.append(predictions)
        weights_list.append(weights)
    return predictions_list, weights_list

# 示例数据
X = np.array([[0, 0], [1, 1], [1, 0], [0, 1]])
Y = np.array([-1, 1, 1, -1])

# 训练
predictions_list, weights_list = adaboost_train(X, Y, 10)

#### 2.3.2 调参与性能优化

AdaBoost算法的调参主要涉及迭代次数、每个弱学习器的类型和参数。一般来说，可以通过交叉验证来确定迭代次数以防止过拟合，同时也可以通过调整弱学习器的参数来优化性能。

from sklearn.model_selection import train_test_split

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2)

# 用训练集进行训练
predictions_list, weights_list = adaboost_train(X_train, y_train, num_classifier=100)

# 使用测试集进行性能评估
final_predictions = combine_predictions(predictions_list, weights_list)

在性能评估阶段，可以使用分类准确度、混淆矩阵、接收者操作特征曲线下面积（AUC）等指标来衡量模型的预测性能。

通过上述章节，我们不仅深入地理解了AdaBoost算法的原理，还实际操作了如何通过编程来实现这一算法，并探讨了在实践中如何对它进行调优。这为AdaBoost算法的实际应用打下了坚实的基础。

# 3. Gradient Boosting算法深入分析

#### 3.1 Gradient Boosting的理论基础

##### 3.1.1 数学推导与优化过程

Gradient Boosting 是一种基于 Boosting 思想的机器学习算法，它通过迭代地添加弱学习器（通常是决策树），并逐步减小残差（残差是实际值与模型预测值之间的差值），最终构建出一个强大的集成模型。 Gradient Boosting 算法的关键在于利用损失函数的负梯度信息来指导每一步的弱学习器的构造。

在数学上，可以将 Gradient Boosting 的优化过程视为求解以下目标函数的最小化问题：

\[ L(y, F(x)) = \sum_{i=1}^{n} l(y_i, F(x_i)) + \Omega(F) \]

其中，\( L \) 是损失函数，\( y \) 是真实值，\( F(x) \) 是模型预测值，\( l \) 是损失函数的表达式，\( \Omega(F) \) 是模型复杂度的正则项（如树模型的叶节点数），\( n \) 是样本数量。

为了最小化上述目标函数，我们采用梯度下降法的思想，即在每一步找到目标函数对模型 \( F \) 的负梯度（即残差），然后对这个负梯度进行拟合，构建新的弱学习器。

##### 3.1.2 损失函数的梯度下降

对于不同的问题（比如分类问题或回归问题），损失函数 \( l \) 的形式会有所不同。在实际应用中，对于回归问题，常用的损失函数包括平方损失和绝对损失；对于分类问题，则常用对数损失。

在构建模型的过程中，每一步都会根据当前模型的预测和真实值计算损失函数的梯度。梯度实际上就是损失函数对预测值 \( F(x) \) 的导数。为了简化问题，我们假设 \( F_0(x) \) 是初始模型（通常为常数），那么对于第 \( m \) 步，我们会更新模型 \( F_m(x) \) 如下：

\[ F_{m}(x) = F_{m-1}(x) - \gamma_m h_m(x) \]

其中，\( \gamma_m \) 是学习率（或步长），\( h_m(x) \) 是第 \( m \) 步的弱学习器，而 \( F_m(x) \) 是经过 \( m \) 步后的模型。

#### 3.2 Gradient Boosting的实现机制

##### 3.2.1 树模型的构建过程

构建树模型时，我们通常采用 CART（分类与回归树）算法，这是一种二叉树结构，每一个叶节点对应一个预测值。在构建树的过程中，我们需要选择最佳分裂点来最大化分割后子节点与父节点的差异。

选择最佳分裂点时，通常使用贪心算法，从所有可能的分割点中选择最佳的分割。对于回归问题，我们通常使用最小化均方误差（MSE）的方法来选择最佳分裂点；对于分类问题，则使用基尼不纯度或交叉熵等方法。

##### 3.2.2 预测与更新策略

在每次迭代结束时，我们会得到一个弱学习器，然