【并行计算加速】：Boosting算法在大数据处理中的应用

# 1. 并行计算的基础概念

## 1.1 并行计算的定义
并行计算是指同时使用多个计算资源解决计算问题的过程。这种计算方式可以显著提高程序的运行效率，特别是在处理大规模数据集时更为明显。通过分配不同的任务到多个处理单元，可以减少总的计算时间，是解决高性能计算问题的核心技术之一。

## 1.2 并行计算的优势
在并行计算中，优势主要体现在两个方面：一是时间效率，多处理器可以并行执行多个任务，减少整体计算时间；二是资源利用，能够充分利用集群或多核处理器的计算能力，提升数据处理的吞吐量。

## 1.3 并行计算的挑战
尽管并行计算有诸多优势，但其实施也面临挑战。首要问题是编程复杂性，开发者需要设计可以并行执行的算法和程序。另外，数据传输和同步开销也可能成为性能瓶颈。因此，如何有效地设计并行算法和管理计算资源成为关键。

# 2. Boosting算法原理及其在大数据中的作用

## 2.1 Boosting算法概述

### 2.1.1 Boosting算法的发展历程

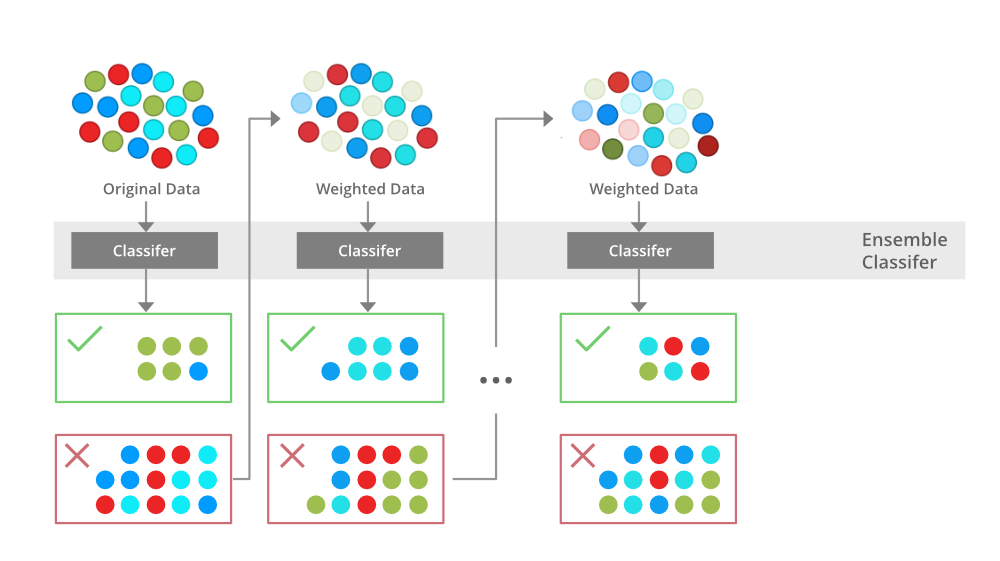
Boosting算法是一系列提升算法的统称，它的核心思想是通过建立多个分类器的组合来提高单个分类器的性能，是机器学习领域的一种重要技术。最早期的Boosting算法，比如Arc-x4，是建立在弱分类器概念上的，这些弱分类器可以是简单的决策树，甚至单层的神经网络。随着理论的成熟和技术的进步，Boosting算法逐渐演变成了更为强大的集成学习方法。1995年，由Yoav Freund和Robert Schapire提出的AdaBoost算法标志着Boosting算法研究的一个里程碑。AdaBoost通过赋予之前分类错误的样本更高的权重来提高后续分类器对这些样本的关注度，通过迭代构建多个分类器，最终通过加权投票的方式组合成一个强分类器。

到了21世纪初，随着梯度提升算法（Gradient Boosting）的提出，Boosting算法进入了一个新的发展时期。这一算法利用损失函数的梯度信息来迭代地改进预测结果，被广泛应用于回归和分类问题。紧接着，由Tianqi Chen等人开发的XGBoost进一步提升了梯度提升算法的计算效率和模型性能，同时实现了模型的正则化，使得模型更加泛化。XGBoost不仅在机器学习竞赛中广受欢迎，也在商业应用中得到广泛应用。

### 2.1.2 Boosting算法的理论基础

Boosting算法的理论基础主要建立在偏差-方差权衡以及弱学习器和强学习器的概念上。偏差-方差权衡指的是一个模型如果过于简单（偏差高）则会欠拟合，反之如果过于复杂（方差大）则会过拟合。Boosting算法试图通过组合多个弱学习器来构建一个强学习器，从而降低整体模型的偏差和方差。

从统计学习的角度看，Boosting算法可以被视作一种最小化经验风险的算法，这里的“经验风险”通常指训练集上的损失函数。每个弱学习器都是基于当前训练集的分布以及之前弱学习器的表现而产生的，进而提升模型的泛化能力。数学上，通过累积错误分类样本权重的方式来确保后续的弱学习器能够更准确地对这些样本进行分类。

此外，Boosting算法在一定程度上可以被看作是半监督学习的特例。这是因为Boosting算法虽然主要依赖有标签的数据集进行训练，但其对数据的重加权方式暗示了对未标记数据的学习。这种对数据重要性不同角度的理解为后续研究者提供了更多优化和创新的空间。

## 2.2 Boosting算法的种类和比较

### 2.2.1 AdaBoost算法原理与实现

AdaBoost（Adaptive Boosting）是Boosting算法中较为经典的一种，它通过调整训练集中各个样本的权重来提高分类器的性能。在AdaBoost算法中，每一轮迭代会根据前一轮分类器的性能来更新样本权重，分类错误的样本会获得更大的权重，以便于下一轮的分类器给予更多关注。通过迭代累加所有分类器的预测结果，最终得到一个强分类器。

从原理上讲，AdaBoost算法的关键在于如何调整权重和如何计算弱分类器的输出。假定数据集有N个样本，第i个样本的权重表示为D(i)，初始时每个样本的权重是相等的。在每一轮t中，构建一个弱分类器h_t，通过分类错误率ε_t来确定下一轮迭代中每个样本的权重D_t+1(i)。权重的更新公式为：

D_t+1(i) = D_t(i) * exp(-α_t * y_i * h_t(x_i))

其中，y_i是样本的真实标签，h_t(x_i)是第t个弱分类器的预测标签，α_t是该弱分类器的权重，其计算公式为：

α_t = 0.5 * ln((1 - ε_t) / ε_t)

当弱分类器建立完成后，最终的强分类器H(x)是所有弱分类器的加权和：

H(x) = sign(Σ(α_t * h_t(x)))

在实现方面，AdaBoost算法通常需要选择合适的弱学习器，如决策树桩（decision stumps），即只能进行单个划分的决策树。此外，需要实现权重更新机制和预测模型的组合策略。

### 2.2.2 Gradient Boosting与XGBoost的演进

随着Boosting算法的发展，梯度提升（Gradient Boosting）算法的提出将Boosting推向了新的高度。梯度提升算法将提升算法与梯度下降法结合起来，每一步都试图最小化损失函数的梯度。这一算法利用损失函数的梯度信息来迭代地改进预测结果，适用于各种不同的损失函数，包括回归问题的均方误差（MSE）损失和分类问题的交叉熵损失等。

梯度提升的关键步骤在于寻找每一步的最优残差预测值。这个预测值是通过最小化当前损失函数关于预测值的梯度得到的。在每次迭代过程中，通过增加一个新的弱学习器来拟合当前损失函数的负梯度。具体来说，如果当前预测值为F_t(x)，那么新的弱学习器h_t(x)应该满足：

h_t(x) = argmin Σl(F_t(x) + h_t(x))

其中，l是损失函数。在实际应用中，常见的损失函数包括平方损失、绝对损失和对数损失等。

XGBoost是梯度提升算法的一种优化实现。它在以下几个方面对传统梯度提升算法进行了创新：

1. 正则化项：XGBoost在目标函数中加入了正则项，用来控制模型的复杂度，防止过拟合。
2. 稀疏感知：在处理缺失值和稀疏数据时，XGBoost能自动学习到处理的策略。
3. 并行化：XGBoost实现了树的分裂算法的近似，从而可以在构建树时使用多线程进行特征选择。
4. 缺失值处理：XGBoost可以自动选择最佳分割点，对含有缺失值的特征进行分割。
5. 可扩展性：XGBoost支持自定义的损失函数，使其可以应用于多种不同的问题。

为了实现这些优化，XGBoost引入了近似算法和并行计算机制，以及对于梯度提升算法在大数据环境下运行效率的改进。接下来，我们详细探讨XGBoost算法的核心机制以及它在大数据背景下的实现。

import xgboost as xgb
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载数据集
data = load_breast_cancer()
X, y = data.data, data