遗传算法核心机制大公开：选择、交叉与变异的最佳实践

# 1. 遗传算法的基本概念与原理

遗传算法是一种模拟自然选择和遗传机制的搜索启发式算法，属于演化计算的一部分。它通过模拟自然遗传学中的“适者生存，不适者淘汰”的原则，对解空间进行高效搜索，以求达到问题的最优解或近似解。

## 遗传算法的历史与发展
遗传算法的概念最早由John Holland教授在上世纪60年代提出，并在70年代得到发展。它受到生物进化理论的启发，通过选择（Selection）、交叉（Crossover）和变异（Mutation）三种基本操作，实现个体的遗传和优化。经过多年的演变，遗传算法已在工程优化、机器学习、人工智能等多个领域得到应用。

## 遗传算法的基本原理
遗传算法在求解问题时，首先将可能的解决方案编码为染色体（通常为二进制串），形成一个初始种群。种群中的每个个体都对应一个适应度（Fitness）值，表示其解决问题的能力。通过迭代选择适应度高的个体参与下一代的生成，经过交叉和变异操作产生新的种群，最终收敛至最优解或满意的解。

# 2. 选择机制的探索与优化

## 2.1 遗传算法中的选择过程
遗传算法（GA）中的选择过程是模拟生物进化中自然选择的过程，它根据个体适应度的高低来决定其遗传到下一代的概率。该过程的核心目标是保留优秀的个体，同时允许那些可能携带有益基因变异的个体有机会传递到后代，以此来保证种群的多样性。

### 2.1.1 选择方法的理论基础
选择机制的基本原理可以概括为以下几点：

1. **选择压力**：这是一种衡量选择机制强度的指标。较高的选择压力意味着适应度高的个体更有可能被选中，较低的选择压力则允许更多的适应度较低的个体有遗传的机会。
2. **适应度保留**：通过某种策略保留一定数量的优秀个体，以避免因随机选择导致优秀基因的丧失。
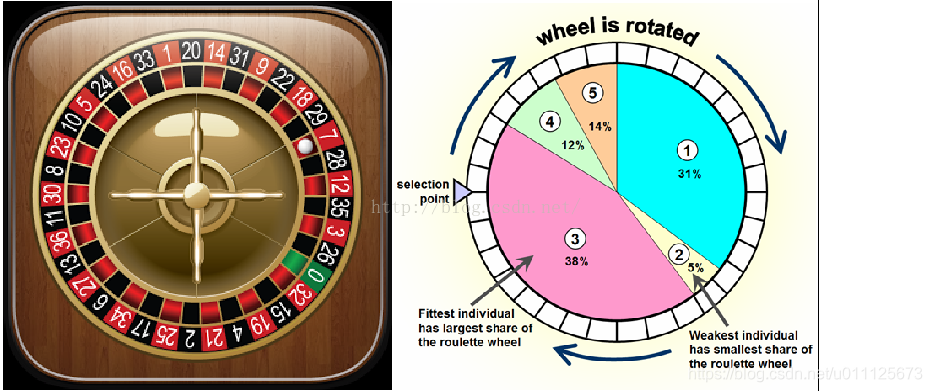
3. **轮盘赌选择（Roulette Wheel Selection）**：在这个策略中，每个个体被选中的概率与其适应度成正比。这可以通过分配一个累积概率来实现，其中每个个体的累积概率是前一个个体的累积概率加上它自己的适应度比例。
4. **锦标赛选择（Tournament Selection）**：在这个方法中，随机选择一组个体，然后从这组个体中选出适应度最高的个体作为父代。

### 2.1.2 选择策略的实践案例
在实际应用中，选择策略的选择往往取决于具体问题的要求。比如在需要快速收敛到最优解的情况下，可能会倾向于使用轮盘赌选择。而在需要保持种群多样性的场合，锦标赛选择可能更加适合。

一个具体的案例是，假设我们正在尝试优化一个旅行商问题（TSP），我们的目标是在保证路径长度最短的前提下访问所有的城市。使用轮盘赌选择时，距离短、适应度高的路径（即总旅行距离短的路径）被选中的概率更高，这有助于算法快速逼近最优解。但是，如果路径短到一定程度，那么种群中几乎所有的路径都将非常相似，从而减少了探索新路径的可能性。在这种情况下，锦标赛选择可以通过允许一些非最优路径被选中来维持多样性。

## 2.2 适应度函数的重要性
适应度函数是衡量个体适应环境能力的标准，它是遗传算法中最重要的部分之一。

### 2.2.1 构建适应度函数的基本原则
构建适应度函数时，需要遵循以下基本原则：

1. **简单性**：适应度函数应该尽可能简单明了，易于计算。
2. **公平性**：不同个体的适应度需要能够反映它们之间在适应环境上的真实差异。
3. **可比性**：需要确保所有个体的适应度可以在同一尺度上进行比较。
4. **相关性**：适应度函数的设计需要紧密地与问题的具体要求相关联。

### 2.2.2 适应度函数的优化技巧
在实践中，适应度函数的优化通常涉及以下几个方面：

1. **归一化**：对于不同量级的特征值进行归一化处理，使适应度函数的计算更加稳定和公平。
2. **惩罚项的添加**：对于不符合问题约束的个体，通过添加惩罚项来降低其适应度，以此来引导种群朝向合法解进化。
3. **动态调整**：适应度函数可以动态调整，以适应算法在不同阶段对多样性和收敛性的需求变化。

例如，在一个调度问题中，适应度函数可能需要综合考虑完成工作的总时间以及可能的延迟，如果目标是最小化总完成时间，并且没有延迟，那么适应度函数可以设计为完成时间的倒数，同时加上一个大的惩罚项来惩罚任何的延迟。

## 2.3 选择机制的性能评估
性能评估是遗传算法设计过程中不可或缺的一步，它可以帮助我们了解所选择的选择机制在特定问题上的表现如何。

### 2.3.1 评估标准与方法
评估选择机制性能的标准通常包括：

1. **收敛速度**：算法达到最优解的速度。
2. **稳定性**：算法在多次运行后得到的解的稳定性。
3. **解的质量**：算法获得的解与真实最优解的接近程度。

评估方法则可以是：

1. **统计分析**：对多次运行算法所得到的解进行统计分析，包括平均值、中位数、标准差等指标。
2. **曲线拟合**：绘制收敛曲线，直观展示算法的收敛过程。

### 2.3.2 选择机制的改进方向
选择机制的改进方向通常依赖于性能评估的结果，潜在的改进方向包括：

1. **自适应选择压力**：根据种群当前的多样性和算法所处的阶段动态调整选择压力。
2. **混合选择方法**：结合多种选择方法的优点，以期达到更好的效果。
3. **集成学习方法**：使用机器学习技术预测个体的未来表现，以此来指导选择过程。

例如，在某些问题中，可以使用机器学习模型来预测哪些个体最有可能产生优秀的后代，并据此调整选择概率，这就是集成学习方法在遗传算法中的应用。

通过这些性能评估方法和改进方向，我们可以对遗传算法中的选择机制进行针对性的优化，以达到更佳的优化效果。

# 3. 交叉策略的设计与实现

## 3.1 交叉过程的理论分析

### 3.1.1 交叉操作的种类与原理

交叉操作是遗传算法中模拟生物遗传中染色体交叉的重要过程。它位于选择过程之后，是算法产生新个体的主要方式。在遗传算法中，交叉操作通常包括单点交叉、多点交叉以及均匀交叉等方法。每种交叉方式都有其特定的适用场景和理论基础。

单点交叉是最常见的一种交叉方式。在这个过程中，一个随机点被选中作为交叉点，然后两个父代染色体从这个点切割开来，交换各自的部分，形成两个新的子代。这种方法简单高效，但可能产生局部最优解。

多点交叉则是单点交叉的扩展，它不仅在两个点上进行切割和交换，而是多个点上进行。这增加了染色体信息交换的多样性，可以更好地模拟自然界中遗传信息的复杂交换过程。

均匀交叉则是另一种形式，它不像前两者那样依赖于特定的点。在这种交叉方式中，每个基因位上的基因来自父代中的哪一