矩阵秩与线性变换：揭示矩阵对向量空间的影响

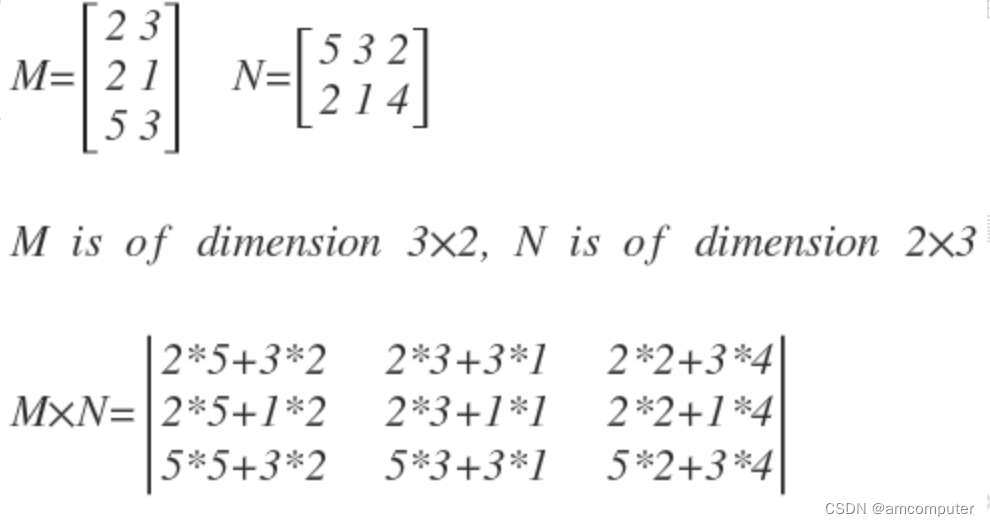
# 1. 矩阵秩的理论基础**

矩阵秩是衡量矩阵线性相关性的重要指标，它反映了矩阵中线性无关行的数量。

**定义：**矩阵 A 的秩，记作 rank(A)，是 A 中线性无关行的最大数量。

**性质：**

* 矩阵的秩等于其行阶梯形的秩。
* 矩阵的秩小于或等于其行数和列数。
* 矩阵的秩不变当且仅当对其进行初等行变换（行交换、行倍加、行倍乘）时。

# 2.1 线性变换的定义和性质

### 2.1.1 线性变换的几何意义

线性变换是一种特殊的函数，它将一个向量空间中的向量映射到另一个向量空间中的向量，并满足以下性质：

- **线性性：**对于任意向量 **x** 和 **y** 以及标量 **a** 和 **b**，有

  T(ax + by) = aT(x) + bT(y)

- **保持向量加法：**对于任意向量 **x** 和 **y**，有

  T(x + y) = T(x) + T(y)

- **保持标量乘法：**对于任意向量 **x** 和标量 **a**，有

  T(ax) = aT(x)

几何上，线性变换可以理解为一个向量空间到另一个向量空间的平移、旋转、缩放或它们的组合。例如，一个二维平面的旋转变换可以将平面上的所有点绕着一个固定点旋转一定角度。

### 2.1.2 线性变换的代数表示

线性变换可以用矩阵来表示。设 **A** 是一个 **m × n** 矩阵，**x** 是一个 **n × 1** 列向量，则线性变换 **T(x)** 可以表示为：

T(x) = Ax

其中，**Ax** 是一个 **m × 1** 列向量，代表变换后的向量。

矩阵 **A** 称为线性变换的表示矩阵。它包含了变换的所有信息，包括变换的类型、方向和幅度。

# 3. 矩阵秩的实际应用**

### 3.1 线性方程组的求解

#### 3.1.1 矩阵秩与线性方程组的解

对于一个线性方程组：

Ax = b

其中 A 是 m×n 矩阵，x 是 n×1 列向量，b 是 m×1 列向量。

矩阵秩与线性方程组的解之间存在以下关系：

- 当矩阵 A 的秩为 n 时，方程组有唯一解。
- 当矩阵 A 的秩小于 n 时，方程组可能有无穷多个解或无解。

#### 3.1.2 矩阵秩与线性方程组的相容性

矩阵秩还可以用来判断线性方程组是否相容。

- 当矩阵 A 的秩等于 m 时，方程组相容。
- 当矩阵 A 的秩小于 m 时，方程组不相容。

### 3.2 子空间的维度与基

#### 3.2.1 子空间的定义和性质

子空间是向量空间的一个子集，它满足以下性质：

- 子空间包含零向量。
- 子空间对于向量加法封闭。
- 子空间对于数乘封闭。

#### 3.2.2 子空间的维度与矩阵秩

一个子空间的维度等于其基的个数。而矩阵秩可以用来求解子空间的基。

对于一个 m×n 矩阵 A，其秩为 r，则 A 的行空间和列空间都是 r 维子空间。

### 3.3 矩阵的正交分解

#### 3.3.1 正交分解的理论基础

正交分解将一个矩阵分解为三个矩阵的乘积：

A = QR

其中：

- A 是 m×n 矩阵
- Q 是 m×m 正交矩阵
- R 是 m×n 上三角矩阵

#### 3.3.2 正交分解的实际应用

正交分解在实际应用中非常广泛，例如：

- 求解最小二乘问题
- 求解线性方程组
- 图像处理
- 数据分析

# 4. 矩阵秩的进阶应用

矩阵秩在计算机科学和工程的各个领域都有着广泛的应用。本章将介绍矩阵秩在图像处理、数据分析和机器学习中的进阶应用。

### 4.1 图像处理中的矩阵秩

#### 4.1.1 图像压缩和去噪

图像压缩是一种减少图像文件大小的技术，而又不显著降低图像质量。矩阵秩在图像压缩中发挥着重要作用。

* **奇异值分解（SVD）：** SVD可以将图像分解为一组奇异值和对应的奇异向量。通过截断较小的奇异值，可以有效地压缩图像，同时保持其主要特征。

import numpy as np
from scipy.linalg import svd

# 读取图像
image = cv2.imread('image.jpg')

# 将图像转换为灰度
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 进行奇异值分解
U, s, Vh = svd(gray_image)

# 截断奇异值
truncated_s = s[:100]

# 重构图像
reconstructed_image = np.dot(U, np.dot(np.diag(truncated_s), V