避免统计陷阱:方差分析(ANOVA)常见错误与规避技巧(专业解读)
发布时间: 2024-11-24 10:37:03 阅读量: 32 订阅数: 21 


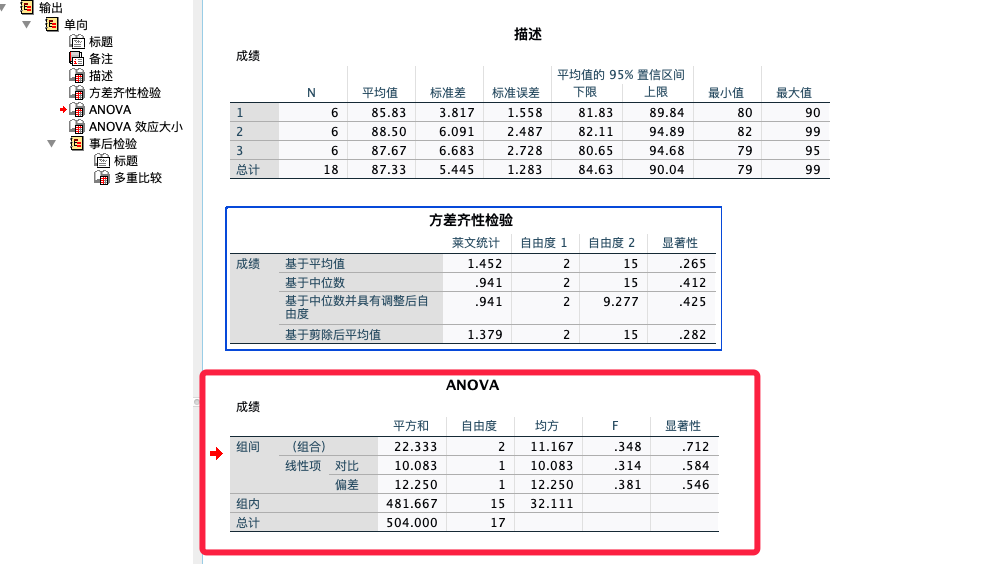
数据分析:R语言详解方差分析ANOVA的计算步骤
# 1. 方差分析(ANOVA)基础
## 方差分析(ANOVA)的定义与目的
方差分析,简称ANOVA,是一种统计方法,主要用于测试三个或三个以上样本均值是否存在显著性差异。它是建立在统计推断理论的基础上,通过比较各组内的方差(组内变异)和各组间的方差(组间变异),来确定组间差异是否显著。使用方差分析,研究者能够在不直接比较所有组别间均值的同时,判断多个群体是否存在系统性的差异。
## 方差分析的重要性
方差分析在统计学和实验设计中扮演着重要的角色。它能够帮助我们:
- 理解数据的变异性和不同因素对结果变量的影响。
- 确定特定因素是否在统计上对观测结果产生了显著影响。
- 为多组数据比较提供一个数学模型,而不是进行多次双样本t检验,减少第一类错误(假阳性)的风险。
## 方差分析的前提假设
进行方差分析时,数据应满足以下假设:
- **正态性**:每个群体数据都应近似正态分布。
- **方差齐性**:所有群体的方差相等。
- **独立性**:样本观测值之间应该相互独立。
了解并满足这些假设是获得有效ANOVA结果的关键。在后续章节中,我们将深入探讨这些概念以及如何处理假设不成立的情况。
# 2. 方差分析的理论基础与实施步骤
## 2.1 方差分析的数学原理
### 2.1.1 假设检验与方差分解
在方差分析(ANOVA)的核心理念中,假设检验是用于判断不同组之间是否存在显著性差异的方法。我们假设各组均值相等,然后使用统计方法去检验这一假设是否成立。数据的总变异性可以分解为两部分:组间变异性(也称作系统变异或处理效应)和组内变异性(随机变异或误差)。
在具体操作中,会计算组间均方(Between-group mean square,MSB)和组内均方(Within-group mean square,MSW)。MSB是组间变异性的均值,而MSW是组内变异性的均值。然后,通过F统计量(F = MSB/MSW)来检验组间均值是否存在显著差异。如果F值较大,表明组间差异大于组内差异,从而拒绝原假设,认为组间存在显著差异。
### 2.1.2 F分布与F检验
F统计量服从F分布,这种分布是由两个卡方分布的比值构成的,它们分别代表组间变异和组内变异的均方。F分布是单尾分布,其形状取决于两个自由度:分子自由度(组间自由度)和分母自由度(组内自由度)。
F检验用于比较两个独立样本方差的比率是否显著不同于1,即检验两个总体方差是否相等。在方差分析中,我们关注的是F值是否显著大于1,从而确定不同组之间是否存在显著差异。
## 2.2 方差分析的类型及应用
### 2.2.1 单因素ANOVA
单因素ANOVA(One-way ANOVA)是最简单的方差分析形式,用于比较三个或以上样本组的均值是否存在显著差异。这种分析假设所有组内数据是独立且方差相等的,组间均值可能不同。
单因素ANOVA的典型应用场景包括比较不同处理条件、不同时间点或不同个体组之间的差异。例如,在农业试验中,可能需要比较不同施肥水平对作物产量的影响。
### 2.2.2 多因素ANOVA
多因素ANOVA(Two-way or Multi-way ANOVA)用于分析两个或多个因素对响应变量的效应。该方法不仅能够检验因素主效应,还能检验因素间的交互作用效应。
举个例子,如果研究人员想研究温度和湿度两个因素对植物生长速率的影响,多因素ANOVA可以帮助他们理解两个因素是否有交互作用,从而决定如何最佳地控制这两个环境因素。
### 2.2.3 重复测量ANOVA
重复测量ANOVA(Repeated Measures ANOVA)用于处理相关样本设计,即同一组受试者在不同时间点或不同条件下的数据。与传统的单因素ANOVA不同,重复测量ANOVA能够控制个体差异对结果的影响,提高统计效率。
一个重复测量ANOVA的典型应用是在心理学实验中,测量同一批受试者在不同心理任务或干预措施前后的反应时间变化。
## 2.3 方差分析的步骤详解
### 2.3.1 数据准备与模型建立
进行方差分析之前,数据收集和预处理是至关重要的。首先要确保数据的质量,包括数据的完整性、准确性以及是否符合方差分析的要求(如正态性、方差齐性等)。
数据准备完毕后,可以建立线性模型来描述响应变量与解释变量之间的关系。在单因素ANOVA中,模型可能为:
```R
Yij = μ + Ti + εij
```
其中,Yij表示第i个组的第j个观测值,μ是总体均值,Ti是第i个组的效应,而εij是误差项。
### 2.3.2 组间与组内变异的计算
在执行方差分析时,主要关注的是组间变异(Between-group variation)和组内变异(Within-group variation)。组间变异反
0
0





