防止随机森林过拟合：模型复杂度控制的黄金策略

# 1. 随机森林模型概述

在机器学习领域，随机森林作为一种集成学习方法，因其卓越的性能和良好的鲁棒性而广受赞誉。它由多个决策树构成，每棵树的构建都采用随机的方式选择特征子集。随机森林通过整合这些决策树的预测结果，能够显著提高预测准确性并降低过拟合的风险。本章将介绍随机森林的基本概念、历史发展以及其在不同应用场景中的优势。

随机森林由 Leo Breiman 和 Adele Cutler 在 2001 年提出。该模型的核心思想是通过构建多棵决策树并进行集成，以获得更好的泛化性能。它解决了单一决策树容易过拟合的问题，因为单一决策树会过度拟合训练数据，导致在未见过的数据上性能下降。而随机森林通过引入随机性，为每棵决策树引入一定的噪声和变化，从而增加了模型的多样性，并且提高了对新数据的适应能力。

在本章中，我们将深入探讨随机森林的算法原理、构建方法和应用场景。同时，也会对随机森林与其他机器学习算法进行对比，说明其为何能在众多算法中脱颖而出，并在分类、回归、特征选择等多个领域大放异彩。通过理解随机森林的基础知识，我们能够为后续章节中深入探讨过拟合问题、模型复杂度控制以及优化策略打下坚实的理论基础。

## 1.1 随机森林的算法原理

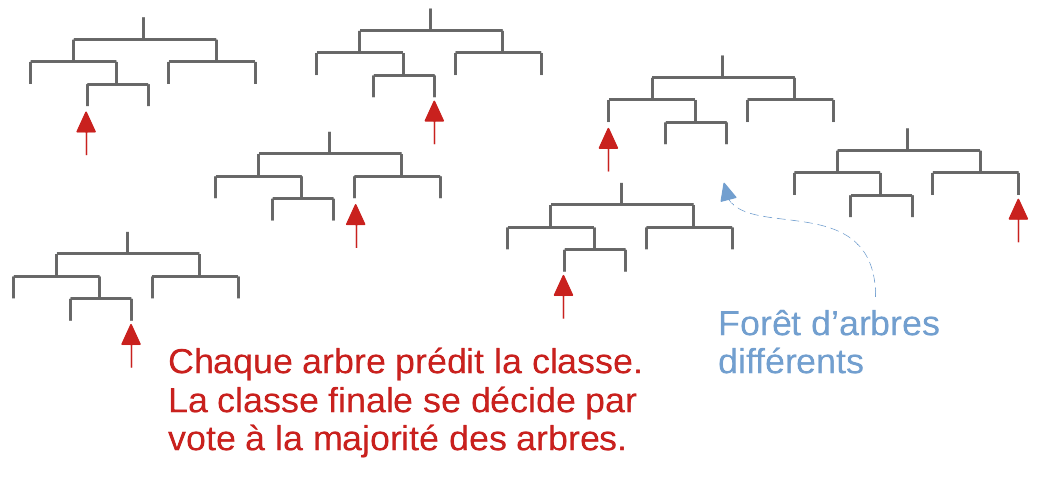
随机森林是一种集成学习算法，它构建多个决策树并将它们的预测结果综合起来以提高整体的准确性和防止过拟合。具体来说，随机森林在生成每棵决策树时，都采用特征的随机子集，这有助于增加树的多样性。在分类任务中，随机森林预测一个样本的类别的方法是通过投票决定，即大多数树所预测的类别被选为最终类别；在回归任务中，则是取所有树预测值的平均。

随机森林通过组合多个弱学习器来形成一个强学习器，其强大之处在于两个关键机制：

- **Bagging：** 这是bootstrap aggregating（自助聚合）的缩写。随机森林通过从原始数据集中有放回地抽样（bootstrap）来生成多个训练数据子集。然后在每个子集上训练独立的决策树，最终通过投票或平均的方式组合这些树的预测结果。Bagging有助于降低模型的方差，从而提高模型的稳定性。

- **特征随机选择：** 当构建决策树时，并不是每次都考虑所有可用的特征，而是仅从原始特征集的一个随机子集中选择特征来进行最佳分割的搜索。这种方法增强了模型的随机性和多样性，同时降低了单棵树之间相关性的风险。

## 1.2 随机森林的历史与发展

随机森林的起源可以追溯到决策树的发展。在20世纪90年代，由于决策树能够提供高度可解释的模型并且对数值和类别数据均有效，因此受到了研究者和实践者的青睐。然而，决策树容易过拟合并且对小的变化非常敏感，这限制了它们在复杂问题上的表现。为了解决这些问题，集成学习技术应运而生。

### 创始人与里程碑

- **Leo Breiman** 和 **Adele Cutler** 在 2001 年正式提出了随机森林算法。Breiman 在机器学习领域因其在决策树和随机森林算法方面的开创性工作而闻名，并在2004年获得了 ACM 小型机计算奖。

- **发展与改进：** 自提出以来，随机森林经历了不断的改进和扩展。研究者们不仅试图进一步减少过拟合，还努力提高模型的计算效率和预测准确率。此外，随机森林在处理大量特征和缺失数据的能力也得到了增强。

### 应用领域

由于随机森林的通用性和有效性，它被应用于包括但不限于：

- **生物信息学：** 在基因表达数据的分类与回归任务中，随机森林显示出了优秀的表现。
- **金融分析：** 用于信用评分、欺诈检测等，因其良好的预测能力和对不平衡数据集的处理能力。
- **环境科学：** 在气候建模和生态建模中，随机森林能够处理大量特征并提供高准确率的预测。

## 1.3 随机森林的应用优势

随机森林算法在解决现实世界问题时拥有以下优势：

- **准确性高：** 随机森林结合了多个决策树的预测，因此在很多情况下，其预测性能要优于单个决策树。
- **健壮性：** 对噪声和异常值具有较好的容忍性，适合处理现实中的复杂数据。
- **过拟合小：** 随机森林中的决策树通过引入随机性来增强模型的泛化能力，降低了过拟合的风险。
- **特征选择：** 随机森林还可以提供特征重要性的评估，有助于后续的特征工程和理解数据结构。
- **并行化：** 由于每棵树是独立构建的，随机森林的训练过程可以高度并行化，提高效率。

在接下来的章节中，我们将深入探讨随机森林模型如何控制其复杂度，并应对过拟合问题，以及如何通过实践中的技巧和策略优化随机森林模型。

# 2. 随机森林的模型复杂度控制理论

在构建机器学习模型时，复杂度控制是确保模型性能的关键步骤。一个模型如果过于简单，可能会导致欠拟合，即模型无法捕获数据中的模式和关系。相反，如果模型过于复杂，可能会导致过拟合，即模型捕捉到了训练数据中的噪声和异常，而无法泛化到新的数据上。随机森林作为一种集成学习方法，通过组合多个决策树来构建更加鲁棒的模型。然而，为了确保模型的泛化能力，对随机森林的复杂度进行控制是必要的。本章将探讨随机森林的模型复杂度控制理论，包括模型复杂度的基本概念、随机森林的内部工作机制，以及控制模型复杂度的策略。

## 3.1 模型复杂度的基本概念

### 3.1.1 过拟合与欠拟合的界定

在机器学习中，过拟合（Overfitting）与欠拟合（Underfitting）是描述模型与数据拟合程度的两个极端。

- **欠拟合**：当一个模型过于简单，它可能无法捕捉数据中的基本结构，导致在训练集和测试集上的性能都不理想。欠拟合的模型通常不能很好地表示数据的内在规律。

- **过拟合**：过拟合是指模型在训练集上学得太“好”，以至于它学习到了训练数据的噪声和偶然的特性，而这些特性在新数据上是不存在的。过拟合的模型在训练集上的表现可能很好，但是在测试集上性能显著下降。

### 3.1.2 模型复杂度与泛化能力的关系

模型复杂度与泛化能力之间存在一种权衡关系，这通常被表述为偏差-方差权衡（Bias-Variance Tradeoff）。模型的复杂度增加，往往导致方差增大，从而可能导致过拟合。而模型复杂度降低，偏差增大，可能会导致欠拟合。因此，控制模型的复杂度，找到合适的偏差与方差之间的平衡点是提升模型泛化能力的关键。

- **偏差（Bias）**：偏差描述了模型预测的准确性，即模型在训练集上的平均预测与真实值之间的偏差。高偏差意味着模型过于简单，无法捕捉数据的真实规律。
- **方差（Variance）**：方差度量了模型对于训练数据的小的变动的敏感程度。高方差意味着模型对于训练数据中的细节过于敏感，容易产生过拟合。

## 3.2 随机森林的内部工作机制

### 3.2.1 随机子空间方法

随机森林算法的核心思想是构建多个决策树，并通过投票机制来选择最合适的预测结果。每个决策树都独立地在原始数据集的一个随机子集上进行训练，这个子集通常是通过有放回的抽样（Bootstrap）来获得的，这种方法称为自助聚集（Bootstrap Aggregating，简称Bagging）。

- **自助聚集（Bagging）**：自助聚集是通过有放回的抽样，从原始数据集中抽取多个子集，并使用每个子集训练出一个独立的模型。最后，通过投票机制或平均预测值来集成所有模型的预测结果。

随机森林中，每棵决策树构建时引入了额外的随机性：

- **特征随机性**：在每次分裂节点时，不是考虑所有特征，而是从所有特征中随机选取一部分特征，然后再找到最佳分裂特征。这种方法称为随机子空间方法。

### 3.2.2 随机森林的构建过程

随机森林的构建过程可以分为以下几步：

1. **从原始数据集中有放回地抽取样本**：对于每个决策树，从原始数据集中抽取n个样本，n是原始数据集的大小。由于是有放回的抽样，因此在每棵树的训练数据集中会有重复的样本，同时也会有未被抽中的样本。

2. **构建单棵决策树**：使用这些抽样数据构建决策树。在每次分裂节点时，随机选择若干个特征，从这些特征中找到最佳分裂特征进行分裂。这种随机性能够增加模型的多样性，降低过拟合的风险。

3. **重复构建多棵决策树**：重复步骤1和2，构建出许多棵独立的决策树，组成随机森林。

4. **输出最终预测结果**：对于分类问题，通过多数投票法决定最终的类别；对于回归问题，预测结果为所有决策树预测值的平均。

## 3.3 控制模型复杂度的策略

### 3.3.1 预剪枝与后剪枝的区别

剪枝（Pruning）是减少决策树复杂度的重要手段。剪枝的过程可以发生在树的构建过程中（预剪枝）或者在树构建完成之后（后剪枝）。

- **预剪枝（Pre-pruning）**：在树的构建过程中，通过提前停止树的增长来控制模型的复杂度。预剪枝基于提前设定的停止准则，例如当树达到一定深度、节点中的样本数低于某个阈值时停止生长。

- **后剪枝（Post-pruning）**：在树完全生长后，根据一定的标准来剪除某些节点。这通常涉及到对树的评估，评估标准可能包括准确率提升、交叉验证分数等。

### 3.3.2 随机森林中的剪枝方法

在随机森林中，虽然单个决策树已经通过引入随机性减少了过拟合的风险，但整个森林模型仍然有可能过拟合。因此，我们可以在构建随机森林的过程中应用剪枝策略：

- **树的深度限制**：可以通过限制每棵树的最大深度来实现预剪枝，从而限制模型的复杂度。

- **节点样本数限制**：设定一个最小节点样本数，当节