传递函数绘制与分析：揭示控制系统动态特性的秘密

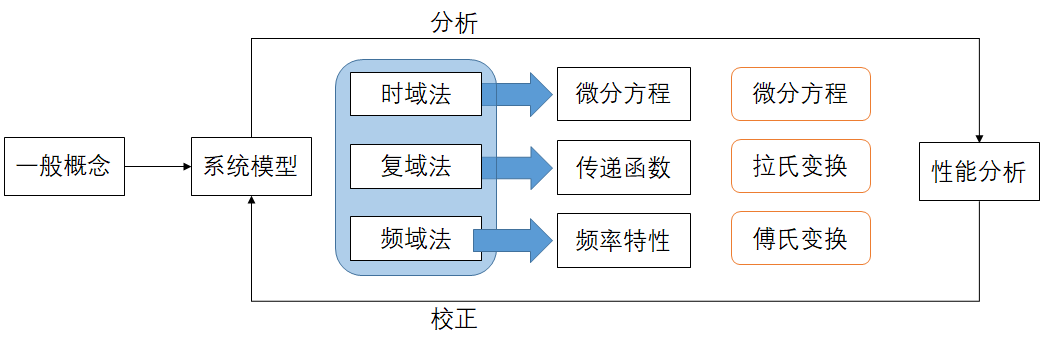
# 1. 传递函数基础

传递函数是表征线性时不变 (LTI) 系统在频域特性的数学工具。它描述了系统输出与输入之间的关系，有助于分析系统的稳定性、性能和设计。

传递函数通常表示为：

H(s) = Y(s) / X(s)

其中：

* H(s) 是传递函数
* Y(s) 是系统的输出信号的拉普拉斯变换
* X(s) 是系统的输入信号的拉普拉斯变换
* s 是拉普拉斯变换的复变量

# 2. 传递函数分析

传递函数分析是研究传递函数的特性和行为，以了解系统在不同输入信号下的响应。传递函数分析分为时域分析和频域分析两种方法。

### 2.1 时域分析

时域分析研究传递函数在时域中的响应，即系统对输入信号的直接响应。

#### 2.1.1 时域响应的获取方法

时域响应可以通过以下方法获取：

- **单位阶跃响应：**将输入信号设置为单位阶跃函数，即在时刻 t=0 之前为 0，在 t=0 时刻突变为 1。系统的时域响应即为单位阶跃响应。
- **单位冲激响应：**将输入信号设置为单位冲激函数，即在时刻 t=0 时刻为无穷大，其他时刻为 0。系统的时域响应即为单位冲激响应。

#### 2.1.2 时域响应的分析和解读

时域响应可以提供以下信息：

- **上升时间：**系统从 10% 上升到 90% 输出值所需的时间。
- **下降时间：**系统从 90% 下降到 10% 输出值所需的时间。
- **峰值时间：**系统输出达到峰值所需的时间。
- **峰值幅度：**系统输出的峰值幅度。
- **稳定时间：**系统输出稳定在最终值附近所需的时间。

### 2.2 频域分析

频域分析研究传递函数在频域中的响应，即系统对不同频率输入信号的响应。

#### 2.2.1 傅里叶变换和拉普拉斯变换

频域分析使用傅里叶变换或拉普拉斯变换将时域信号转换为频域信号。

- **傅里叶变换：**将时域信号转换为频率域信号，其中频率为实数。
- **拉普拉斯变换：**将时域信号转换为复频域信号，其中频率为复数。

#### 2.2.2 频率响应的获取和解读

频率响应可以通过以下方法获取：

- **幅频响应：**表示传递函数在不同频率下的幅度变化。
- **相频响应：**表示传递函数在不同频率下的相位变化。

频率响应可以提供以下信息：

- **截止频率：**传递函数幅度衰减到 3dB 时的频率。
- **共振频率：**传递函数幅度达到峰值的频率。
- **相位裕度：**传递函数相位在截止频率处的裕度。
- **增益裕度：**传递函数幅度在截止频率处的裕度。

# 3.1 绘制传递函数幅频响应

#### 3.1.1 Bode图的绘制方法

Bode图是一种半对数坐标图，横轴表示频率，纵轴表示幅值（增益）和相位。绘制Bode图时，需要将传递函数化简为标准形式：

G(s) = K * (s^n / (s^m + a_1s^(m-1) + ... + a_m))

其中，K为增益，n和m为整数，a_i为常数。

根据传递函数的标准形式，可以绘制Bode图的幅频响应：

- **低频段（ω << 1）：**当频率远小于极点时，传递函数的幅值约为K。
- **高频段（ω >> 1）：**当频率远大于零点时，传递函数的幅值约为K * (ω^n / ω^m) = K * ω^(n-m)。
- **拐点频率：**当频率等于极点或零点时，传递函数的幅值发生20dB/decade的下降或上升。

#### 3.1.2 Bode图的解读和应用

Bode图可以用来分析传递函数的幅频特性，包括：

- **增益：**Bode图的幅值曲线表示传递函数的增益，可以看出系统在不同频率下的放大或衰减程度。
- **带宽：**Bode图的幅值曲线与0dB线相交的频率称为带宽，表示系统能够有效传递信号的频率范围。
- **共振频率：**对于具有复数极点的传递函数，Bode图的幅值曲线会出现峰值，峰值对应的频率称为共振频率。
- **稳定性：**Bode图可以用来判断系统的稳定性。如果幅值曲线在0dB线以下有相交点，则系统不稳定。

# 4. 传递函数综合应用

### 4.1 控制系统稳定性分析

#### 4.1.1 奈奎斯特稳定判据

奈奎斯特稳定判据是一种图形化的方法，用于判断控制系统的稳定性。该判据基于闭环传递函数的奈奎斯特图，即闭环传递函数幅频响应和相频响应在复平面上绘制的曲线。

**奈奎斯特稳定判据的步骤：**

1. 绘制闭环传递函数的奈奎斯特图。
2. 确定开环传递函数的极点和零点。
3. 沿单位圆逆时针方向移动，计算奈奎斯特图与实轴的交点数量。
4. 如果奈奎斯特图与实轴的交点数量等于开环传递函数极点的数量，则系统稳定。
5. 如果奈奎斯特图与实轴的交点数量大于开环传递函数极点的数量，则系统不稳定。

**代码示例：**

import numpy as np
import ma