贝叶斯推断在教育领域的应用：学生评估与教学策略优化

# 1. 贝叶斯推断概述**

贝叶斯推断是一种统计方法，它将先验知识与观测数据相结合，以更新对未知参数或事件概率的信念。与传统的频率主义统计不同，贝叶斯推断考虑了不确定性，并允许在获得新信息时更新概率估计。

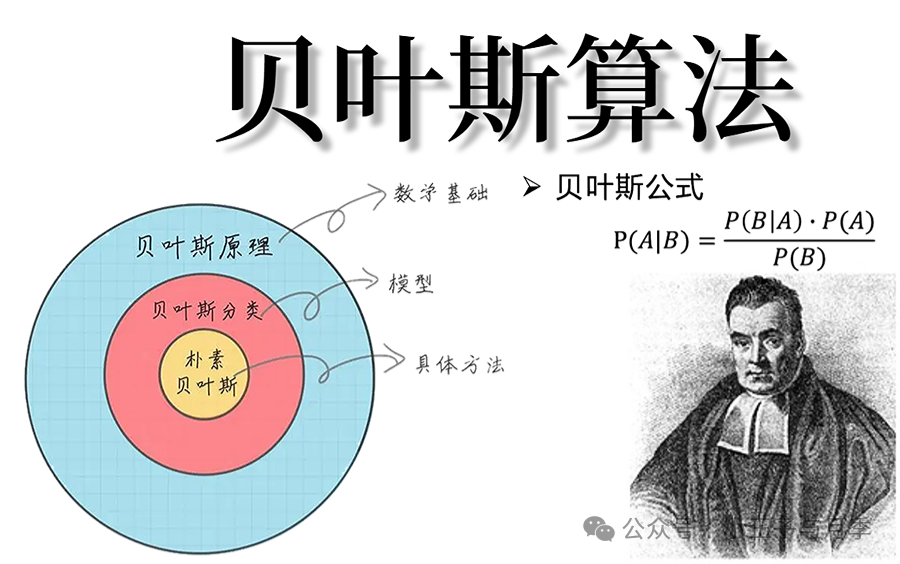
贝叶斯定理是贝叶斯推断的基础。它表示在已知条件 A 的情况下，事件 B 发生的概率为：

P(B | A) = (P(A | B) * P(B)) / P(A)

其中：

* P(B | A) 是在已知条件 A 的情况下事件 B 发生的概率。
* P(A | B) 是在事件 B 发生的情况下条件 A 为真的概率。
* P(B) 是事件 B 的先验概率。
* P(A) 是条件 A 的先验概率。

# 2. 贝叶斯推断在学生评估中的应用

### 2.1 基于贝叶斯网络的学生能力评估

**概述**

贝叶斯网络是一种概率图模型，用于表示变量之间的依赖关系。在学生评估中，贝叶斯网络可以用来构建学生能力模型，该模型可以捕获学生对不同知识领域的掌握程度。

**流程**

1. **定义变量：**确定要评估的学生能力领域，例如数学、阅读和科学。
2. **建立网络结构：**使用专家知识或数据分析来确定不同能力领域之间的依赖关系。
3. **指定先验概率：**根据先验知识或数据，为每个能力领域指定初始概率分布。
4. **收集证据：**收集学生在不同任务或评估中的表现数据。
5. **更新概率：**使用贝叶斯更新规则将证据与先验概率相结合，更新学生能力的概率分布。

**代码示例**

import pybayesnet

# 定义变量
variables = ["Math", "Reading", "Science"]

# 建立网络结构
network = pybayesnet.Network()
network.add_links(("Math", "Reading"), ("Math", "Science"), ("Reading", "Science"))

# 指定先验概率
network.set_probability("Math", {"Low": 0.3, "Medium": 0.5, "High": 0.2})
network.set_probability("Reading", {"Low": 0.4, "Medium": 0.4, "High": 0.2})
network.set_probability("Science", {"Low": 0.5, "Medium": 0.3, "High": 0.2})

# 收集证据
evidence = {"Math": "High", "Reading": "Medium"}

# 更新概率
network.update(evidence)

# 输出后验概率
print(network.get_probability("Science"))

**逻辑分析**

* `pybayesnet`库用于构建和操作贝叶斯网络。
* `add_links`方法指定网络结构，其中箭头表示变量之间的依赖关系。
* `set_probability`方法为每个变量指定先验概率分布。
* `update`方法将证据与先验概率相结合，更新网络中变量的概率分布。
* `get_probability`方法返回指定变量的后验概率分布。

### 2.2 贝叶斯方法的考试评分和学生分类

**概述**

贝叶斯方法可以用于考试评分和学生分类，因为它可以考虑学生的先验知识和考试表现的不确定性。

**流程**

1. **建立贝叶斯模型：**使用贝叶斯网络或其他概率模型来表示学生能力和考试表现之间的关系。
2. **收集数据：**收集学生的考试成绩和其他相关数据，例如先前的评估或人口统计信息。
3. **估计参数：**使用贝叶斯推断技术，估计模型中的参数，例如学生能力的先验分布和考试表现的条件概率。
4. **预测学生能力：**使用估计的参数，根据学生的考试表现预测他们的能力。
5. **对学生进行分类：**根据预测的学生能力，将学生分为不同的类别，例如熟练、中等或初学者。

**代码示例**

import numpy as np
from scipy.stats import norm

# 建立贝叶斯模型
prior = norm(loc=0, scale=1)  # 学生能力的先验分布
likelihood = norm(loc=0, scale=1)  # 考试表现的条件概率

# 收集数据
scores = np.array([70, 85, 90, 65, 80])

# 估计参数
posterior = prior.copy()
for score in scores:
    posterior *= likelihood.pdf(score)

# 预测学生能力
ability