贝叶斯优化：高效搜索超参数，加速机器学习模型开发

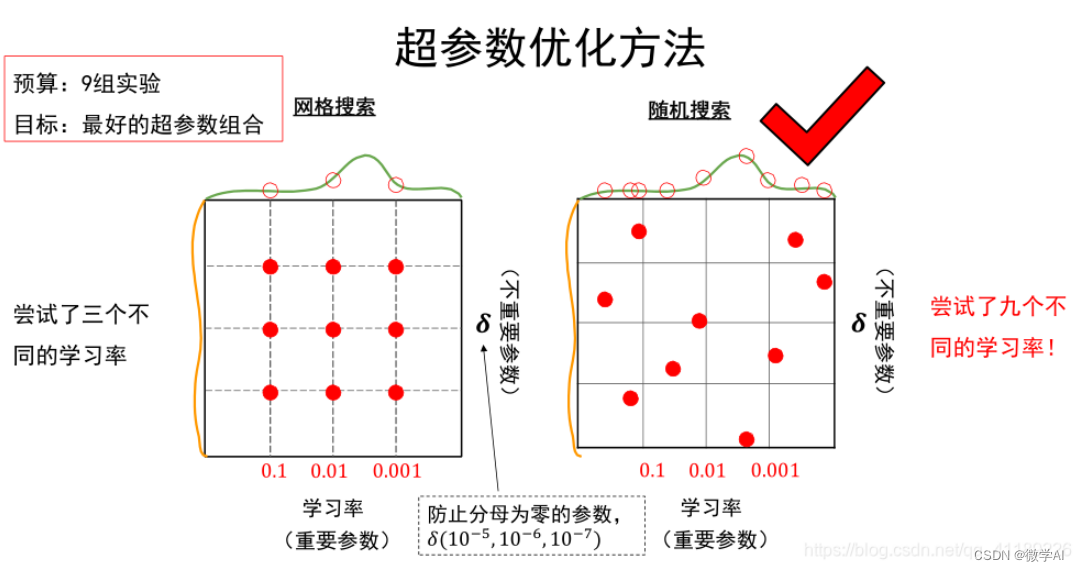
# 1. 贝叶斯优化的概念和原理

贝叶斯优化是一种基于贝叶斯统计的优化算法，它通过迭代方式不断更新目标函数的后验分布，从而找到最优解。其核心思想是利用高斯过程回归模型对目标函数进行建模，并通过采集策略和模型更新两个步骤不断优化模型。

贝叶斯优化算法的流程如下：

1. 初始化高斯过程回归模型，并设置初始超参数。
2. 根据采集策略选择下一个采样点。
3. 在采样点处评估目标函数，并更新高斯过程回归模型。
4. 重复步骤 2 和 3，直到达到终止条件。

# 2. 贝叶斯优化算法的实现和应用

### 2.1 高斯过程回归模型

#### 2.1.1 高斯过程回归的原理

高斯过程回归（GPR）是一种非参数贝叶斯回归模型，它将函数建模为高斯过程。高斯过程是一种概率分布，它描述了函数在输入空间中的分布。在 GPR 中，函数被建模为一个具有均值函数和协方差函数的高斯分布。

均值函数表示函数的预期值，协方差函数表示函数在不同输入点之间的协方差。通过指定均值函数和协方差函数，我们可以定义高斯过程。

#### 2.1.2 高斯过程回归的超参数

GPR 的超参数是定义高斯过程的均值函数和协方差函数的参数。常见的超参数包括：

- **长度尺度超参数（l）：**控制协方差函数的平滑度。较大的长度尺度超参数会导致更平滑的函数，而较小的长度尺度超参数会导致更粗糙的函数。
- **振幅超参数（σ）：**控制函数的方差。较大的振幅超参数会导致函数具有较大的方差，而较小的振幅超参数会导致函数具有较小的方差。
- **噪声超参数（ε）：**控制观测值中噪声的方差。较大的噪声超参数会导致模型对噪声更鲁棒，而较小的噪声超参数会导致模型对噪声更敏感。

### 2.2 贝叶斯优化算法流程

贝叶斯优化算法是一个迭代算法，它通过以下步骤进行：

#### 2.2.1 采集策略

在每一步中，贝叶斯优化算法使用采集策略选择下一个要评估的输入点。常见的采集策略包括：

- **期望改进（EI）：**选择具有最大预期改进的输入点。EI 衡量了在给定输入点处采样函数的潜在好处。
- **概率改进（PI）：**选择具有最大概率改进的输入点。PI 衡量了在给定输入点处采样函数并获得比当前最佳值更好的值的概率。
- **上置信界（UCB）：**选择具有最大上置信界的输入点。UCB 衡量了在给定输入点处采样函数并获得良好值的可能性。

#### 2.2.2 模型更新

一旦选择了输入点，贝叶斯优化算法就会使用观测值更新 GPR 模型。更新后的模型将用于在下一步中选择输入点。

### 2.3 贝叶斯优化算法的应用

贝叶斯优化算法广泛应用于各种领域，包括：

#### 2.3.1 超参数调优

贝叶斯优化算法可用于调优机器学习模型的超参数。超参数是模型训练过程中不直接学习的参数，例如学习率和正则化系数。通过使用贝叶斯优化算法，我们可以找到最佳的超参数组合，从而提高模型的性能。

#### 2.3.2 黑盒函数优化

贝叶斯优化算法可用于优化黑盒函数，即我们不知道函数的解析形式的函数。通过使用贝叶斯优化算法，我们可以找到黑盒函数的最佳输入值，从而获得最佳输出值。

# 导入必要的库
import numpy as np
import GPy

# 定义目标函数（黑盒函数）
def objective_function(x):
    return np.sin(x) + np.random.normal(0, 0.1)

# 定义输入空间
input_space = np.li