MATLAB非线性拟合在机器学习中的应用：模型训练，预测更准确

# 1. 非线性拟合的概念和原理**

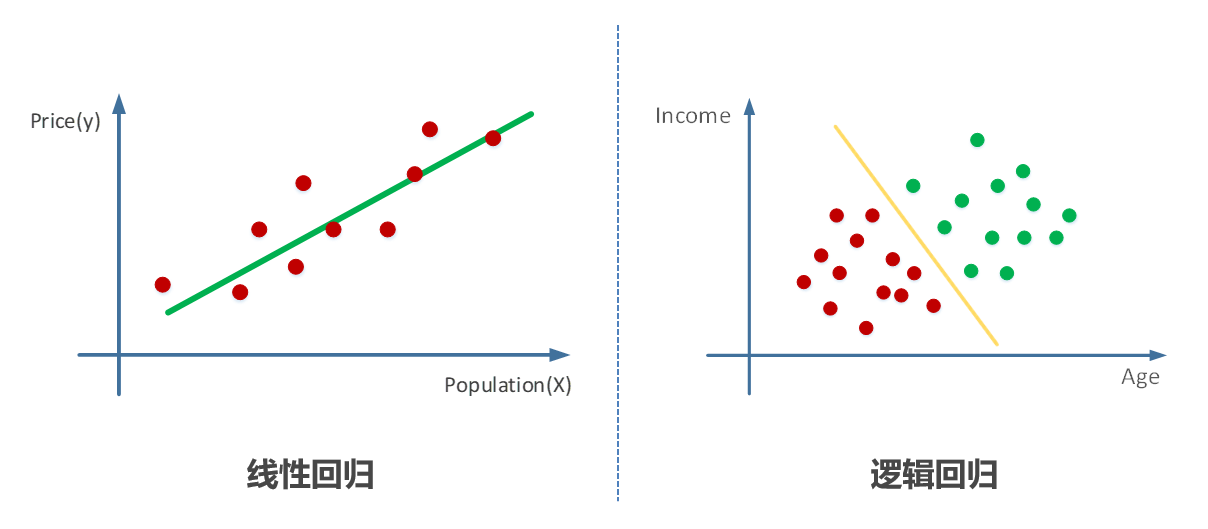
非线性拟合是一种用于拟合非线性关系数据的技术。与线性拟合不同，非线性拟合允许数据点之间存在更复杂的关系。非线性关系通常用数学函数表示，例如多项式、指数函数或对数函数。

非线性拟合的原理是找到一个函数，该函数最适合给定的数据点。这通常通过最小化函数和数据点之间的误差来实现。常用的误差度量包括均方误差 (MSE) 和平均绝对误差 (MAE)。

非线性拟合在机器学习中具有重要意义，因为它允许模型捕获数据中的复杂关系。通过使用非线性函数，机器学习模型可以更准确地预测和分类数据。

# 2. MATLAB中的非线性拟合方法

### 2.1 基于最小二乘法的非线性拟合

最小二乘法是一种经典的非线性拟合方法，其目标是找到一组模型参数，使得模型预测值与观测值之间的平方误差最小。在MATLAB中，可以使用`fminsearch`函数进行基于最小二乘法的非线性拟合。

% 定义非线性模型函数
model_func = @(x, p) p(1) * exp(-p(2) * x);

% 生成观测数据
x_data = linspace(0, 10, 100);
y_data = model_func(x_data, [1, 0.5]) + 0.1 * randn(size(x_data));

% 定义目标函数（平方误差）
objective_func = @(p) sum((model_func(x_data, p) - y_data).^2);

% 初始猜测参数
initial_guess = [1, 0.5];

% 使用fminsearch进行最小二乘法拟合
options = optimset('Display', 'iter');
[optimal_params, fval] = fminsearch(objective_func, initial_guess, options);

% 拟合结果
disp('Optimal parameters:');
disp(optimal_params);
disp('Objective function value:');
disp(fval);

### 2.2 基于最大似然估计的非线性拟合

最大似然估计是一种统计方法，其目标是找到一组模型参数，使得模型预测值与观测值之间的似然函数最大。在MATLAB中，可以使用`mle`函数进行基于最大似然估计的非线性拟合。

% 定义非线性模型函数
model_func = @(x, p) p(1) * exp(-p(2) * x);

% 生成观测数据
x_data = linspace(0, 10, 100);
y_data = model_func(x_data, [1, 0.5]) + 0.1 * randn(size(x_data));

% 定义似然函数
likelihood_func = @(p) prod(normpdf(y_data, model_func(x_data, p), 0.1));

% 初始猜测参数
initial_guess = [1, 0.5];

% 使用mle进行最大似然估计拟合
options = optimset('Display', 'iter');
[optimal_params, fval] = mle(likelihood_func, initial_guess, options);

% 拟合结果
disp('Optimal parameters:');
disp(optimal_params);
disp('Objective function value:');
disp(fval);

### 2.3 基于贝叶斯方法的非线性拟合

贝叶斯方法是一种概率方法，其目标是找到一组模型参数的后验分布，该分布基于观测数据和先验信息。在MATLAB中，可以使用`bayesopt`函数进行基于贝叶斯方法的非线性拟合。

% 定义非线性模型函数
model_func = @(x, p) p(1) * exp(-p(2) * x);

% 生成观测数据
x_data = linspace(0, 10, 100);
y_data = model_func(x_data, [1, 0.5]) + 0.1 * randn(size(x_data));

% 定义先验分布
prior_func = @(p) normpdf(p(1), 1, 0.5) * normpdf(p(2), 0.5, 0.25);

% 定义似然函数
likelihood_func = @(p) prod(normpdf(y_data, model_func(x_data, p), 0.1));

% 定义后验分布
posterior_func = @(p) prior_func(p) * likelihood_func(p);

% 初始猜测参数
initial_guess = [1, 0.5];

% 使用bayesopt进行贝叶斯拟合
options = optimset('Display', 'iter');
[optimal_params, fval] = bayesopt(posterior_func, initial_guess, options);

% 拟合结果
disp('Optimal parameters:');
disp(optimal_params);
disp('Objective function value:');
disp(fval);

# 3. 非线性拟合在机器学习中的应用**

### 3.1 非线性回归模型的建立

非线性回归模型旨在拟合具有非线性关系的数据。在MATLAB中，可以使用以下函数建立非线性回归模型：

model = fitnlm(X, y, 'modelfun', 'myfun');

其中