YOLOv8特征提取背后的数学：揭秘算法的深层逻辑

# 1. YOLOv8算法概述

YOLOv8，作为目标检测领域的最新成员，继承并发扬了YOLO系列算法快速、准确的传统。它不仅在速度上进行了优化，还显著提升了检测精度。YOLOv8的设计理念是实现高效率与高精度的平衡，目标是在实时系统中提供最佳的检测性能。

## 1.1 算法的演进历程
YOLOv8并没有简单地沿用早期版本的架构，而是融合了近年来深度学习领域的众多创新技术。算法的演进历程反映了从YOLOv1到YOLOv8的不断迭代和对速度与精度权衡的追求。

## 1.2 核心优势分析
本节将深入剖析YOLOv8的核心优势，包括但不限于其改进的网络结构、增强的特征提取机制，以及如何通过高效的设计理念来实现更快的推理速度和更高的检测准确率。通过与前代版本和其他竞争算法的对比，我们揭示了YOLOv8在多个基准测试中取得突破的内在逻辑。

## 1.3 应用场景展望
YOLOv8的推出不仅对学术界产生了巨大影响，对工业界的应用也有深远的意义。它在视频监控、自动驾驶、医疗影像分析等领域展现了巨大潜力。本节将探讨YOLOv8在不同场景下的应用可能性和实际效益。

# 2. YOLOv8的数学基础

## 2.1 卷积神经网络数学原理

### 2.1.1 卷积操作的数学模型

在深度学习领域，卷积神经网络（CNN）是处理图像数据的强大工具，其核心操作之一就是卷积。卷积操作在数学上可以表示为一个函数（图像）与另一个函数（卷积核或滤波器）的互相关运算。具体来说，给定输入数据 \( X \) 和卷积核 \( K \)，卷积结果 \( Y \) 的数学表达式为：

\[ Y(i,j) = (K * X)(i,j) = \sum_m \sum_n K(m,n) \cdot X(i+m, j+n) \]

在这个过程中，\( X \) 代表输入的多维数组，例如图像；\( K \) 是卷积核，是一个小的二维数组；\( Y \) 是通过卷积操作得到的输出结果，也就是特征图（feature map）。

卷积操作的关键在于卷积核的移动和权重的应用，每一个卷积核都可以捕捉到输入数据中的某些特征。通过学习，网络能够自动地找到对当前任务最有用的特征表示。

### 2.1.2 激活函数的作用与类型

激活函数在神经网络中起到非线性映射的作用，使得网络可以拟合复杂的非线性关系。如果没有非线性激活函数，无论多少层的网络，最终都可以被一个单层线性网络所等效，这将大大限制网络的表达能力。

常见的激活函数有：

- **Sigmoid**：输出范围在 0 到 1 之间，函数表达式为 \( \sigma(x) = \frac{1}{1 + e^{-x}} \)。尽管其历史悠久，但现在因为梯度消失问题已不太常用。
- **ReLU (Rectified Linear Unit)**：\( f(x) = max(0, x) \)。ReLU 激活函数简单且计算效率高，目前广泛应用于各种深度学习模型中，不过也存在"死亡ReLU"的问题。
- **Leaky ReLU**：作为 ReLU 的改进版本，Leaky ReLU 通过引入一个小的斜率来解决死亡ReLU问题。如果 \( x < 0 \)，\( f(x) = \alpha x \)，否则 \( f(x) = x \)。
- **Softmax**：通常用于多分类问题的输出层，将输出转换为概率分布。Softmax 的表达式为 \( \sigma(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}} \)，其中 \( z_i \) 为输出层的第 \( i \) 个神经元的输入值。

理解这些激活函数的工作原理及其适用场景对于构建高效网络至关重要。

## 2.2 深度学习中的优化方法

### 2.2.1 损失函数的选择与应用

损失函数（或称代价函数）衡量的是模型预测值与真实值之间的差距，是训练神经网络时需要最小化的对象。损失函数的选择对模型的训练效果有着直接的影响。

对于不同的任务，适用的损失函数也不尽相同：

- **回归任务** 常用的损失函数是均方误差（MSE）或均方根误差（RMSE）。
- **二分类问题** 通常使用二元交叉熵损失。
- **多分类问题** 常见的损失函数包括交叉熵损失（当输出层使用softmax激活函数时）。

选择合适的损失函数是优化网络性能的关键步骤之一。

### 2.2.2 反向传播与梯度下降

反向传播和梯度下降是深度学习中训练模型的基石，它们一起工作，通过逐步调整网络中的参数来最小化损失函数。

- **反向传播** 是一种算法，用于计算损失函数相对于网络权重的梯度。这个过程开始于输出层，逐步向输入层回传误差信号，从而可以计算每个权重对最终损失的影响。
- **梯度下降** 是一个迭代优化算法，用于更新网络中的权重。通过计算损失函数关于权重的梯度，然后以这个梯度的负方向移动权重一小步，可以逐渐减小损失。

梯度下降的多种变体（如随机梯度下降、批量梯度下降和小批量梯度下降）在实际应用中有着不同的优缺点。

反向传播和梯度下降算法的结合使得深度学习模型可以自动调整其内部参数，以达到学习数据表示的目的。这为构建高性能的深度学习模型提供了可能。

本章对YOLOv8的数学基础进行了深入的剖析，为理解其背后的原理打下了坚实的基础。接下来的章节将进一步探讨YOLOv8的核心特性，包括特征提取机制、网络结构以及实际应用。

# 3. YOLOv8的特征提取机制

## 3.1 特征提取的流程

### 3.1.1 特征图的生成

在深度学习中，特征提取是目标检测模型的核心环节之一。YOLOv8作为一款先进的实时目标检测系统，它在特征提取上采用了多层次的抽象方式。特征图的生成主要通过一系列卷积层和池化层的堆叠来实现。

卷积层通过卷积核（滤波器）在输入图像上滑动，计算每个位置的响应，以此捕获局部特征。在YOLOv8模型中，不同尺度的卷积核有助于提取不同尺度的特征信息。比如，小尺度的卷积核能够捕捉图像中的细粒度特征，而大尺度的卷积核则善于提取大范围内的特征，这对于检测不同大小的目标至关重要。

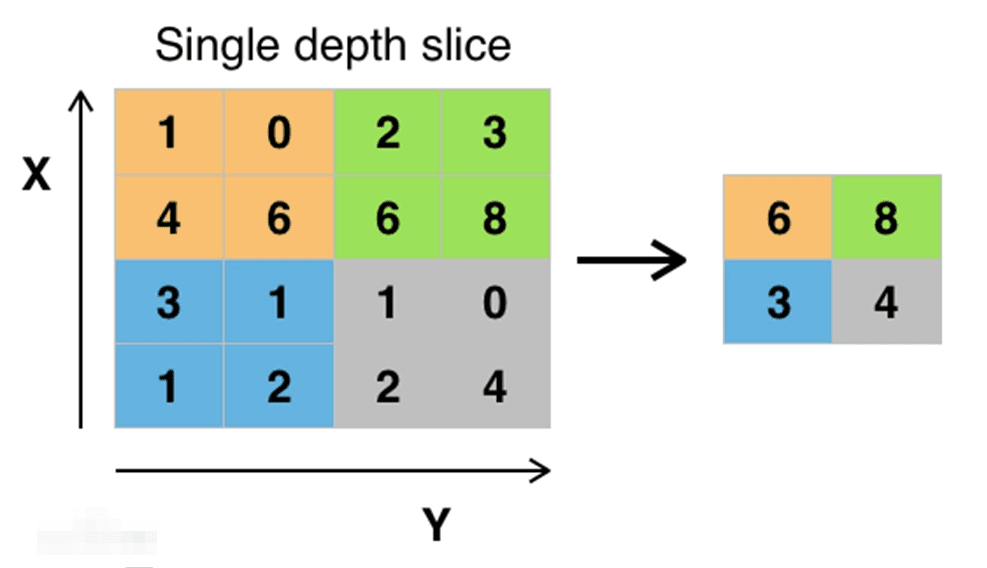
池化层则主要起到降低特征图维度的作用，它通过最大池化或平均池化来实现。这一过程有助于减少计算量，并且能够提供一定程度的平移不变性，这对于后续目标的定位和分类非常有帮助。

### 3.1.2 特征金字塔网络（FPN）

特征金字塔网络（Feature Pyramid Network，FPN）是一种用于构建多尺度特征表示的技术。在YOLOv8模型中，FPN的引入进一步强化了模型对大小变化的目标进行检测的能力。

FPN的核心思想是从深层网络中选取不同阶段的特征图，并通过上采样和融合的方式构建一个由粗到细的特征金字塔。具体来说，FPN会选取较深层的特征图（具有较强语义信息）进行上采样，然后将其与较浅层的特征图（具有较好空间信息）进行融合。这个过程可以迭代进行，生成不同尺度的特征表示。

FPN的优势在于它能够保持较低层的细节信息，同时结合高层的语义信息，使得在不同尺度上都能够检测到目标，这对于检测小目标尤其重要。

### 3.1.3 特征金字塔网络（FPN）的代码实现

下面是一个简化的FPN的代码示例，展示了如何通过PyTorch框架实现特征金字塔网络的基本结构。

import torch
import torch.nn as nn
import torch.nn.functional as F

class PyramidFeatures(nn.Module):
    def __init__(self, C3_size, C4_size, C5_size, feature_size=256):
        super(PyramidFeatures, self).__init__()
        self.P5_1 = nn.Conv2d(C5_size, feature_size, kernel_size=1, stride=1)
        self.P5_upsampled = nn.Upsample(scale_factor=2, mode='nearest')
        self.P5_2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=1)
        self.P4_1 = nn.Conv2d(C4_size, feature_size, kernel_size=1)
        self.P4_upsampled = nn.Upsample(scale_factor=2, mode='nearest')
        self.P4_2 = nn.Conv2d(feature_size, feature_s