【数据结构全解】：前端开发者必备指南

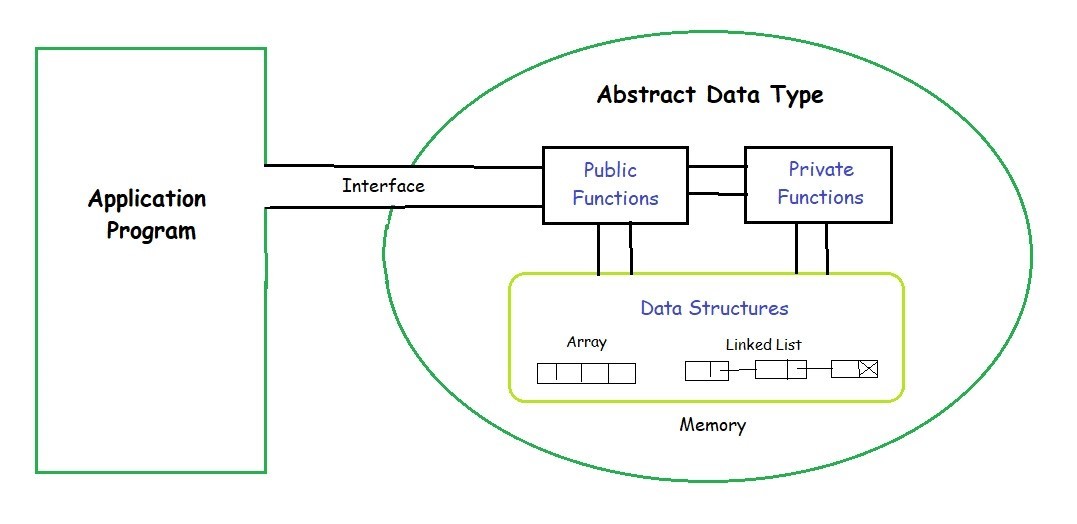
# 1. 数据结构在前端开发中的重要性

在前端开发中，数据结构是构建高效、可维护代码的基础。它不仅涉及到直接的性能优化，还涉及到用户界面的响应速度和交互逻辑的简洁性。前端开发者必须理解并熟练运用各种数据结构来应对不断变化的业务需求和挑战。

## 1.1 数据结构的作用与优势

数据结构提供了组织数据的多种方式，使前端开发者能够在不同场景中选择最合适的数据组织形式。比如，利用栈来处理浏览器历史记录的后退和前进功能，或使用树形结构优化复杂的DOM操作。

## 1.2 数据结构与前端性能

合理选择数据结构可以极大地提升前端性能。例如，使用散列表（Hash Table）可以加快数据查询速度，从而优化页面加载时间。在实际开发中，前端工程师需要结合具体问题来决定使用哪种数据结构。

## 1.3 数据结构在前端框架中的应用

在现代前端框架中，如React或Vue，数据结构被用于构建响应式系统。组件的状态树是一种特定的数据结构，它影响到渲染逻辑和性能。深入理解数据结构，可以帮助开发者更好地掌握这些框架的工作原理。

通过本章节的学习，前端工程师将会对数据结构有一个全面的认识，并理解它在前端开发中的重要性，从而在实际工作中能够更高效地处理数据和优化应用性能。

# 2. 线性数据结构基础

### 2.1 数组和字符串操作

#### 2.1.1 数组的定义和基本操作

数组是一种线性数据结构，它可以存储一系列相同类型的元素。在前端开发中，数组是处理数据流、存储列表、用户输入等场景的基础。数组的定义和基本操作包括初始化、添加、删除、遍历等。

let myArray = []; // 初始化一个空数组
myArray.push('element'); // 添加元素
let removedElement = myArray.pop(); // 删除并返回最后一个元素
myArray.forEach((element, index) => console.log(`Element at index ${index} is ${element}`)); // 遍历数组

数组操作的逻辑分析：
- `push`方法用于在数组的末尾添加一个或多个元素，并返回新的长度。
- `pop`方法用于移除数组的最后一个元素，并返回被移除的元素。
- `forEach`方法为数组中的每个元素执行一次提供的函数。

#### 2.1.2 字符串处理技巧

字符串可以看作是字符数组的特殊形式。在前端开发中，字符串处理是常见的需求，例如文本编辑、URL解析等。

let myString = 'Hello, world!';
let index = myString.indexOf('world'); // 查找子字符串的位置
let newString = myString.slice(index); // 提取从指定位置开始到结束的子字符串

字符串处理的逻辑分析：
- `indexOf`方法用于查找子字符串在主字符串中的位置，如果未找到，则返回-1。
- `slice`方法用于提取字符串的某个部分，并返回新的字符串。

### 2.2 链表和队列的应用

#### 2.2.1 链表的概念和实现

链表是一种由一系列节点组成的集合，每个节点包含数据部分和指向下一个节点的指针。链表的优点在于动态添加和删除元素。

class ListNode {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

let node1 = new ListNode('Head');
let node2 = new ListNode('Next');
node1.next = node2; // 链表的创建和连接

链表实现的逻辑分析：
- `ListNode`类定义了链表节点的结构，每个节点包含一个值和一个指向下一个节点的指针。
- 链表的创建涉及实例化节点对象并使用指针连接它们。

#### 2.2.2 队列的操作和应用场景

队列是一种先进先出（FIFO）的数据结构，前端中常用于处理异步任务、事件监听等场景。

class Queue {
  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  enqueue(value) {
    const newNode = new ListNode(value);
    if (this.tail) {
      this.tail.next = newNode;
    }
    this.tail = newNode;
    if (!this.head) {
      this.head = newNode;
    }
    this.size++;
  }

  dequeue() {
    if (!this.head) return null;
    const value = this.head.value;
    this.head = this.head.next;
    this.size--;
    return value;
  }
}

队列操作的逻辑分析：
- `enqueue`方法用于在队列的末尾添加一个新节点。
- `dequeue`方法用于移除队列的头部节点。

### 2.3 栈的使用和原理

#### 2.3.1 栈的基本概念和特性

栈是一种后进先出（LIFO）的数据结构，用于管理函数调用、历史记录等场景。栈的操作主要包含推送（push）、弹出（pop）、查看栈顶（peek）等。

class Stack {
  constructor() {
    this.collection = [];
  }

  push(value) {
    this.collection.push(value);
  }

  pop() {
    return this.collection.pop();
  }

  peek() {
    return this.collection[this.collection.length - 1];
  }
}

栈操作的逻辑分析：
- `push`方法用于在栈顶添加一个元素。
- `pop`方法用于移除并返回栈顶元素。
- `peek`方法用于返回栈顶元素但不移除它。

#### 2.3.2 栈在前端开发中的实际应用

在前端开发中，栈可用于管理页面历史（浏览器的后退、前进按钮）、处理递归函数调用等。

const browserHistory = new Stack();
browserHistory.push('/page1');
browserHistory.push('/page2');
browserHistory.pop(); // 返回到 /page1

栈的实际应用逻辑分析：
- 创建一个`Stack`实例来模拟浏览器历史记录。
- 使用`push`方法来模拟页面跳转。
- 使用`pop`方法来模拟浏览器后退按钮操作。

以上章节已经涵盖了数组、字符串、链表、队列和栈等线性数据结构的基础定义、原理和在前端中的应用。接下来的章节将进一步探讨树形数据结构、图结构以及排序算法等，在前端开发中的应用与实践。

# 3. 树形数据结构与前端

## 3.1 二叉树的遍历和应用

### 3.1.1 二叉树的创建和遍历算法

二叉树是一种常见的树形数据结构，每个节点最多有两个子节点，分别是左子节点和右子节点。二叉树的遍历算法是数据结构与算法中的基础知识点，它涉及到递归或迭代的方式来访问树中的每一个节点。

创建二叉树的最直观方式是通过节点的连接。一个简单的二叉树节点可以这样定义：

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

# 创建一个简单的二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

遍历二叉树通常有三种方式：前序遍历、中序遍历和后序遍历。它们的区别在于访问根节点的顺序不同：

- 前序遍历：先访问根节点，然后访问左子树，最后访问右子树。
- 中序遍历：先访问左子树，然后访问根节点，最后访问右子树。
- 后序遍历：先访问左子树，然后访问右子树，最后访问根节点。

下面是一个前序遍历的递归实现：

def preorder_traversal(root):
    if root is not None:
        print(root.value)       # 访问根节点
        preorder_traversal(root.left)  # 遍历左子树
        preorder_traversal(root.right) # 遍历右子树

### 3.1.2 前端中树结构的实际案例

在前端开发中，树形结构的应用场景非常广泛，如组件的属性配置、文件系统的展示、权限管理的结构等。实际上，React 的虚拟 DOM 树就是一个典型的树形结构，其更新过程也依赖于树的遍历。

以文件系统目录为例，我们可以用二叉树来表示文件夹和文件的层级关系。每一级目录可以视为树的一个节点，子目录或文件作为该节点的子节点。展示这种结构时，通常使用递归组件来实现：

function TreeNode({ node }) {
    return (
        <div>
            <span>{node.name}</span>
            <div>
                {node.children.map(childNode => (
                    <TreeNode node={childNode} key={childNode.id} />
                ))}
            </div>
        </div>
    );
}

这个简单的组件递归地渲染子节点，直到没有子节点为止，从而在页面上展示完整的目录结构。

## 3.2 堆和优先队列

### 3.2.1 堆的定义和性质

堆（Heap）是一种特殊的完全二叉树。在堆中，父节点的值总是不大于（或不小于）其子节点的值，这样的堆称为最小堆（Min-Heap）或最大堆（Max-Heap）。堆是优先队列（Priority Queue）的一种实现方式。

堆的性质可以总结为以下几点：

- 完全二叉树：除了最后一层外，其它每一层都被完全填满，且最后一层的节点都集中在左边。
- 堆属性：对于每个非叶子节点的值，都满足“父节点 <= 子节点”（最小堆）或“父节点 >= 子节点”（最大堆）。

创建一个最小堆可以按照以下步骤进行：

class MinHeap:
    def __init__(self):
        self.heap = []

    def insert(self, value):
        self.heap.append(value)
        self._bubble_up(len(self.heap) - 1)

    def _bubble_up(self, index):
        parent_index = (index - 1) // 2
        if index > 0 and self.heap[parent_index] > self.heap[index]:
            self.heap[parent_index], self.heap[index] = self.heap[index], self.he