自动优化的未来：PID参数自整定技术详解（价值型+专业性）


# 摘要
PID（比例-积分-微分）控制器是工业控制中广泛使用的一种调节装置，其自整定技术可以提高系统性能，减少人工调整的需要。本文首先介绍了PID控制器与自整定技术的基本概念，接着深入探讨了PID控制器的工作原理和参数调整方法，并评估了控制器性能。文章重点分析了自整定技术在实际应用中的实现，常见问题的解决方法，以及工业应用案例。随后，文章讨论了PID自整定技术的性能优化策略和当前面临的挑战。最后，本文展望了自整定技术的未来发展趋势和行业影响，提供了研究结论和对未来技术发展的建议。通过本文的综述，旨在为自动化控制领域提供一套全面的理论和实践指南。

# 关键字
PID控制器；自整定技术；参数调整；性能评估；工业应用案例；优化与挑战

参考资源链接：[冯少辉深度解析：PID整定理论与实战操作指南](https://wenku.csdn.net/doc/7ozsrh0ien?spm=1055.2635.3001.10343)
# 1. PID控制器与自整定技术概述

在自动化控制系统领域，PID控制器是一种历史悠久且应用广泛的反馈控制器，它通过比例（P）、积分（I）和微分（D）三个环节来实现精确控制。然而，传统手动调整PID参数的方法效率低下且难以适应复杂的控制环境，因此自整定技术应运而生，它能够根据系统动态自动调整PID参数以达到最佳控制效果。本章将简要介绍PID控制器及其自整定技术的基本概念，为后续章节深入探讨打下基础。

# 2. PID控制器理论基础

## 2.1 PID控制器的工作原理

### 2.1.1 比例（P）控制的原理与作用
比例控制是PID控制器中最简单的部分，它的核心思想是根据当前的偏差（即期望值与实际值之间的差距）来调节控制器的输出。具体来说，控制器的输出与偏差成正比。比例控制器（P控制器）的输出可以表示为：

\[ u(t) = K_p \cdot e(t) \]

其中，\( u(t) \) 是控制器的输出，\( K_p \) 是比例增益，而 \( e(t) \) 则是偏差。

比例控制的作用可以简要概括为以下几点：

- **偏差调整**：比例控制能确保系统尽快响应偏差，并调整输出以减小偏差。
- **稳定作用**：合适的比例增益可以保持系统稳定，过大的比例增益可能导致系统振荡，过小则可能导致系统响应迟缓。
- **比例带宽度**：比例带是指输出变化为满量程变化时输入偏差的范围，宽度越小，控制器越敏感。

### 2.1.2 积分（I）控制的原理与作用
积分控制关注的是偏差随时间的累积影响，其目的在于消除稳态误差，即当系统进入稳态后，偏差将被完全消除。积分控制器（I控制器）的输出可以表示为：

\[ u(t) = K_i \int_0^t e(\tau) d\tau \]

这里，\( K_i \) 是积分增益，而积分的计算涉及从控制器开始工作到当前时间 \( t \) 的所有偏差累积。

积分控制的作用包括：

- **消除稳态误差**：通过累积偏差，积分控制推动输出变化，最终使得系统的实际输出与期望输出一致。
- **减缓系统响应**：积分作用的加入使得系统响应速度通常会慢于纯比例控制，因为需要时间累积足够的偏差来产生足够的控制作用。
- **系统稳定**：与比例控制类似，积分控制的增益也需要适当设置，过大的积分作用可能导致系统过冲或振荡。

### 2.1.3 微分（D）控制的原理与作用
微分控制考虑的是偏差变化率，其作用是预测偏差的发展趋势，从而提前进行调整以避免系统响应过冲。微分控制器（D控制器）的输出可以表示为：

\[ u(t) = K_d \frac{de(t)}{dt} \]

其中，\( K_d \) 是微分增益，表示系统对偏差变化率的敏感度。

微分控制的作用体现在以下几个方面：

- **减小或避免振荡**：通过分析偏差的变化率，微分控制能预测偏差的未来趋势，从而提前调整控制器输出来对抗振荡。
- **提高响应速度**：微分控制可以加快系统对误差变化的响应，从而使系统更快地回到稳定状态。
- **限制系统响应速度**：过强的微分控制可能会对系统的自然噪声作出过度反应，导致输出过于敏感。

## 2.2 PID参数的调整方法

### 2.2.1 传统调整方法概述
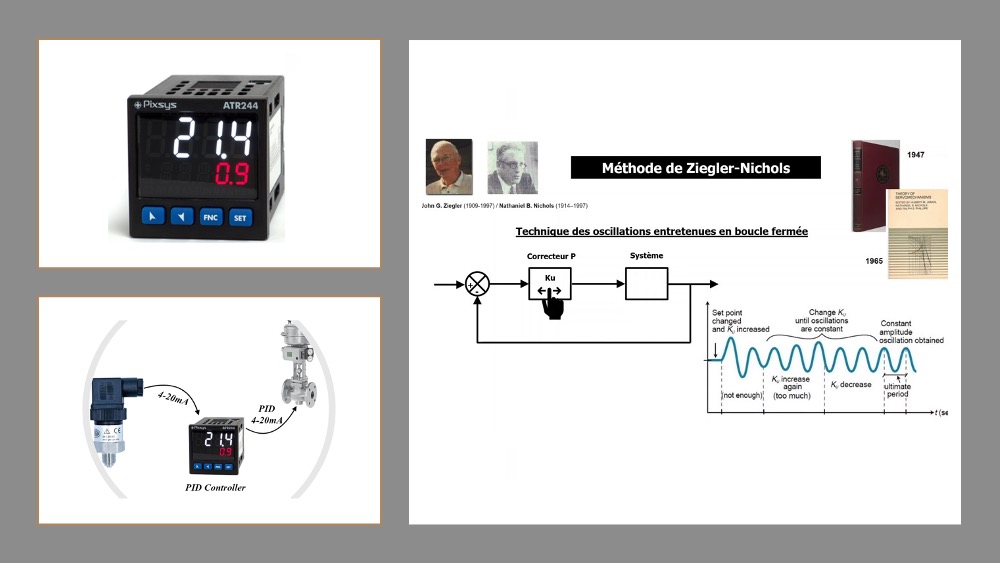
在实际应用中，PID参数的调整通常有几种传统方法。最著名的是“凑试法”（又称为Ziegler-Nichols方法），该方法通过观察系统在特定输入下的响应来设置PID参数。

- **开环测试**：首先对系统进行开环测试，通过系统对阶跃输入的响应来判断系统的类型和时间常数。
- **闭环测试**：之后在闭环状态下进行测试，依据系统的动态响应特征逐步调整PID参数直到获得满意的结果。常见的调整有：
- 先仅开启比例控制，逐渐增加比例增益直到系统开始持续振荡。
- 记录此时的比例增益和振荡周期，作为下一步调整积分和微分参数的基础。

凑试法简单易行，但依赖于操作者的经验和直觉，对于复杂的或者非线性系统可能不够准确。

### 2.2.2 基于模型的调整方法
基于模型的调整方法需要对系统的动态特性有一个数学描述，通常是一组微分方程或传递函数。通过这些模型，可以使用如根轨迹法、频率响应法等方法进行参数调整。

- **根轨迹法**：通过分析开环传递函数的极点随某个参数变化的轨迹，确定使得系统稳定且性能良好的PID参数。
- **频率响应法**：系统闭环频率响应的增益和相位被用来确定最佳的PID参数。

基于模型的方法更加系统化，需要一定的数学工具支持，对于模型不准确或难以建立的系统可能不太适用。

### 2.2.3 基于优化算法的调整方法
随着计算机技术的发展，基于优化算法的PID参数调整方法变得更加可行。这些方法通过构建一个性能指标（如最小化误差的平方和），然后使用优化算法找到最优的PID参数。

- **梯度下降法**：利用性能指标的梯度信息迭代调整PID参数，直到找到最小化误差的参数组合。
- **遗传算法**：通过模拟自然选择过程进行全局搜索，找到一组使性能指标最优的PID参数。
- **粒子群优化**（PSO）：粒子群优化模拟鸟群的觅食行为，通过个体之间的信息交流来寻找最优解。

基于优化算法的方法可以处理更复杂的性能指标和约束条件，尤其适用于那些难以用传统方法解决的问题。

## 2.3 PID控制器的性能评估

### 2.3.1 稳定性分析
稳定性是PID控制器设计中最重要的指标之一。一个稳定的控制系统能够保证在受到扰动时，系统最终回到稳定状态。

- **Routh-Hurwitz判定法**：通过构造一个特征方程，然后使用Routh-Hurwitz准则来判断系统的稳定性。
- **Nyquist稳定准则**：利用系统闭环传递函数的频率响应曲线与复平面上的单位圆进行分析，判断系统的稳定性。

### 2.3.2 过渡过程分析
过渡过程（如上升时间、峰值时间、超调量和调整时间）能够反映系统的快速响应能力以及避免过冲的能力。

- **上升时间**：系统响应达到最终稳态值的一定比例所需的时间。
- **峰值时间**：系统输出达到其峰值所需的时间。
- **超调量**：系统输出超过期望稳态值的最大量。
- **调整时间**：系统输出达到并保持在稳态误差界限内的时间。

### 2.3.3 抗干扰能力评估
抗干扰能力评估反映了系统在面对外部干扰和内部噪声时的稳定性和准确性。

- **扰动响应**：系统对于外部扰动的响应情况，好的抗干扰系统应该能够快速抑制扰动的影响。
- **噪声抑制**：系统对传感器噪声或测量误差的抑制能力，通常通过频域分析来评估。

在PID控制器的性能评估中，通常结合仿真和实验结果来综合判断控制器的效果。通过对这些性能指标的分析，可以更好地理解PID控制器的行为，并指导参数的调整和优化。

# 3. PID参数自整定技术实践

## 3.1 自动化自整定技术的实现

自动化自整定技术是实现PID控制器智能化的重要手段，它涉及算法的选择、数据的实时监控、控制器与执行机构的有效交互等多个环节。自整定技术的核心是通过自动调节PID参数来适应被控对象和外部环境的变化，以达到最优的控制效果。

### 3.1.1 自整定算法的选择与实现

自整定算法的选择直接影响着控制器的性能。目前有多种自整定算法，如Ziegler-Nichols方法、Cohen-Coon方