PID控制秘籍：冯少辉老师揭示整定与优化的终极指南（权威性+实用型）


# 摘要
PID控制是工业自动化领域中应用最为广泛的控制策略，其原理基于比例、积分、微分三个控制环节来调整控制对象，达到快速、准确、稳定的控制效果。本论文详细解释了PID控制原理，并分析了其在控制系统中的应用。文章进一步探讨了传统PID控制器的参数整定方法，以及在实践中调整技巧的重要性。在先进优化策略方面，探讨了现代算法如模糊PID和自适应PID在提高系统性能方面的应用，并关注了实时系统中的PID优化技术。此外，本论文还涵盖了PID控制系统的调试、性能评估以及故障排除方法，最后探讨了智能控制技术与PID结合的未来趋势以及工业应用的扩展。

# 关键字
PID控制原理；参数整定；先进优化策略；性能评估；智能控制；工业应用

参考资源链接：[冯少辉深度解析：PID整定理论与实战操作指南](https://wenku.csdn.net/doc/7ozsrh0ien?spm=1055.2635.3001.10343)
# 1. PID控制原理详解

## 1.1 PID控制概念
PID（比例-积分-微分）控制是一种闭环控制策略，广泛应用于工业过程中保持设备性能稳定。通过调整比例、积分、微分三个参数来响应偏差的变化，实现输出值与设定值之间的最佳匹配。

## 1.2 PID的工作原理
PID控制器通过误差信号（设定值与测量值之差）的比例（P）、积分（I）和微分（D）三个组成部分来计算控制信号。具体来说：
- 比例部分（P）产生与当前误差成正比的输出，用于减小误差。
- 积分部分（I）累计误差随时间变化的总和，用于消除稳态误差。
- 微分部分（D）预测误差的变化趋势，实现快速响应。

## 1.3 PID控制算法的数学表达
数学上，PID控制器的输出（u）可以用以下公式表示：
\[ u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau) d\tau + K_d \frac{de(t)}{dt} \]
其中，\( K_p \)、\( K_i \)和\( K_d \)分别是比例、积分和微分增益，\( e(t) \)为当前误差，\( t \)为时间。

PID控制原理是控制系统设计和调整的基础，深入理解这一原理对于掌握其参数整定和优化至关重要。在下一章中，我们将探讨PID控制器的参数整定，以及如何选择合适的值以获得理想的控制性能。

# 2. PID控制器的参数整定

## 控制系统理论基础

### 系统动态特性的理解

在深入探讨PID参数整定之前，我们必须先对控制系统的基本理论有所了解。控制系统的动态特性通常由其响应来描述，这涉及到系统如何随着时间变化而响应输入的变化。一个系统的动态特性可以通过其阶跃响应来观察，该响应描述了系统从静止状态开始到达到稳定状态的全过程。阶跃响应通常包含以下几个关键参数：

- 上升时间（Rise Time）：系统从初始状态到达最终稳态值的50%到90%所需时间。
- 峰值时间（Peak Time）：系统响应达到第一个峰值所需时间。
- 调整时间（Settling Time）：系统响应进入并保持在最终稳态值一定范围内所需的时间。
- 最大超调量（Overshoot）：系统响应超过最终稳态值的最大值。

理解这些特性对于确定控制器性能目标至关重要。例如，一个快速上升时间和短调整时间可以表示系统的响应快，而一个较小的超调量则可能指示系统具有较好的稳定性。

### 控制目标的确定与分析

在控制系统的设计中，定义清晰的控制目标是至关重要的。这些目标可能包括快速响应、最小超调、高稳定性和良好的抗扰动能力。控制目标的确定需要对控制系统所要实现的实际应用进行深入分析。

例如，在温度控制系统中，目标可能是使温度尽快达到设定值，并保持温度的稳定，同时对电源波动和其他外部因素造成的扰动具有一定的抵抗能力。在控制系统中，我们通常利用数学模型来描述系统的动态行为，如传递函数或状态空间表示法。

在确定控制目标之后，必须对系统进行建模，以便于进行控制器的设计。一个典型的控制系统的模型可能包含一个或多个积分器，这些积分器在时间上累积误差，并产生相应的控制动作以纠正误差。

## 传统PID参数整定方法

### Ziegler-Nichols方法

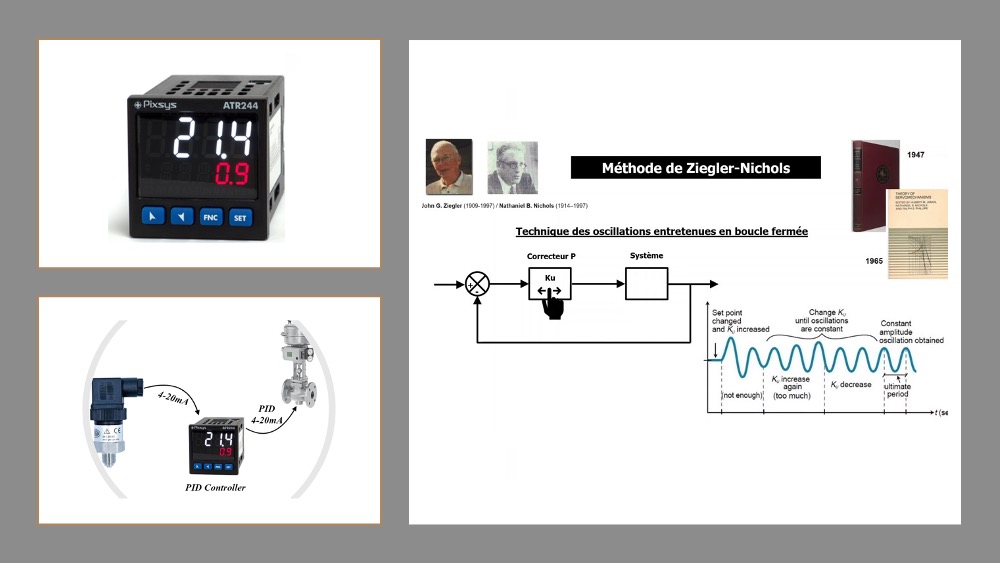
Ziegler-Nichols方法是一种被广泛使用的方法，它基于经验规则，旨在找到一组适合特定控制系统的PID参数。该方法包含两个主要步骤：

1. **临界增益确定**：首先，将比例项（P）单独增加，直到系统进入持续振荡状态。记录此时的比例增益（Ku）和振荡周期（Pu）。

2. **参数设定**：接着根据Ziegler-Nichols表设定PID参数。这需要使用以下公式：

- Kp = 0.6 * Ku
- Ki = 2 * Kp / Pu
- Kd = Kp * Pu / 8

这种方法简单易用，但它基于某些假设，可能会在非线性或有时间延迟的系统中产生次优的性能。

### Cohen-Coon方法

Cohen-Coon方法是一种相对较为复杂的PID参数调整方法，它考虑了系统的开环响应，并提供了调整积分和微分参数的具体指导。以下是基本步骤：

1. **开环测试**：首先，需要进行一个开环测试，以获得系统的时间常数（T）、死区时间（L）和开环增益（K）。

2. **参数设定**：然后使用这些参数结合Cohen-Coon公式来计算PID控制器参数。这种调整方法特别适合于时间延迟系统。

- Kp = (0.9 * K * T) / (L + 0.3 * T)
- Ti = (3.33 * L * T) / (0.3 * T - L)
- Td = (L * T) / (11 * L + 2.5 * T)

这种方法能够较为准确地计算出满足特定性能目标的PID参数，但其复杂的计算和需要的测试可能会增加实际应用中的难度。

## PID参数的调整技巧与实践

### 基于响应曲线的参数调整

基于响应曲线的参数调整方法主要依赖于对系统阶跃响应的分析。通过观察系统响应，可以手动调整PID参数以达到所需的性能。

- **增加Kp（比例增益）**：这通常会缩短上升时间，增加系统的反应速度。
- **增加Ki（积分增益）**：这有助于消除稳态误差，但过高的Ki可能导致系统不稳定和过大的超调。
- **调整Kd（微分增益）**：增加Kd可以帮助减少超调和提高系统的快速响应。

参数调整应该是一个逐步迭代的过程，通过观察系统响应的变化来调整参数，并不断重复此过程，直到达到满意的控制性能。

### 实际工况下的参数微调

在实际工况中，由于外部条件的变化和系统特性的非线性，固定的PID参数可能无法始终保持理想的控制性能。此时，可能需要采用一些在线调整（Adaptive Control）技术。

- **切换控制模式**：根据系统当前的工作状态和环境条件，切换不同的PID参数集。
- **实时监测和反馈**：利用传感器实时监测系统性能，并结合反馈机制动态调整PID参数。
- **引入智能算法**：应用模糊逻辑控制器（FLC）或神经网络来自动调整PID参数，提高系统的自适应能力。

## 总结

在本章节中，我们深入了解了PID控制器参数整定的基本理论和方法，包括经典的传统方法如Ziegler-Nichols和Cohen-Coon方法，以及基于响应曲线的手动调整和在实际工况下的在线调整技巧。理解这些方法对于实现有效的系统控制至关重要，这将为下一步深入探索PID控制的先进优化策略打下坚实的基础。

# 3. PID控制的先进优化策略

## 3.1 先进PID控制算法

### 3.1.1 比例-积分-微分（PID）算法

比例-积分-微分（PID）算法是控制理论中最基本且应用广泛的反馈控制算法。理解PID算法的工作原理对于优化控制系统至关重要。传统PID算法中的三个主要组成部分，比例（P）、积分（I）和微分（D），各自对应不同的控制作用。

- **比例（P）项**：产生与偏差成比例的控制作用，偏差是指期望输出与实际输出之间的差异。比例项的主要作用是减少系统响应的稳态误差，但同时它也是产生超调和振荡的原因。
- **积分（I）项**：对过去一段时间内的偏差进行累积和运算，目的是消除稳态误差，保证系统在长时间运行后能准确地达到设定值。
- **微分（D）项**：预测系统未来的行为，它对偏差变化的速率进行响应，增加系统的阻尼作用，有助于减小超调和振荡。

### 3.1.2 模糊PID和自适应PID算法

随着控制系统复杂度的增加，传统PID算法在某些应用中可能不再满足需求。因此，研究者们开发了各种先进PID算法以提升系统性能。

- **模糊PID控制算法**：模糊逻辑是处理不确定性问题的有效工具。在模糊PID控制中，PID参数不是固定的，而是根据模糊逻辑动态调整。模糊规则基于经验知识，系统会根据输入（如误差和误差变化率）模糊化，再通过模糊规则库进行推理，最后反模糊化为PID参数的调整值。

- **自适应PID控制算法**：自适应控制算法能够自动调整PID参数，以适应系统动态特性的变化。在实际应用中，当被控对象的特性发生变化或受到未知干扰时，自适应PID控制器能够调整参数，使得系统保持良好的控制性能。

## 3.2 实时系统中的PID优化技术

### 3.2.1 实时数据处理和反馈调整

实时系统中，数据的即时处理和反馈调整是优化PID控制器性能的关键。为了实现这一点，系统需要具备快速的数据采集、处理能力和高效的数据反馈机制。

- **数据采集**：现代传感器技术提供了高频率数据采集的可能性，但同时也要求控制器能够快速处理这些信息。高性能的处理器和优化的软件设计是处理高速数据流的基础。

- **实时反馈调整**：系统设计需确保测量误差可以实时反馈到控制器，并且控制器能够快速响应这些反馈，调整输出以纠正误差。反馈机制的设计应尽量减少延迟，并确保数据的准确性和可靠性。

### 3.2.2 故障诊断与系统冗余

在实时系统中，故障诊断和系统冗余是提高系统可靠性和持续运行能力的重要手段。

- **故障诊断**：通过分析系统状态和输出，实现故障检测和隔离。这可能涉及算法监控控制动作和系统响应，以及使用软件进行趋势分析和预测性维护。

- **系统冗余**：在关键应用中，通过在系统中实施冗余组件（如主/备控制器）来提供故障容错能力。这样，即使主要系统出现故障，冗余系统也能接管控制，保证系统的连续运行。

## 3.3 软件实现与模拟工具应用

### 3.3.1 编程实现PID控制

实现PID控制在软件层面意味着需要精心设计算法并将其编码为可执行程序。编程实现PID控制通常涉及以下几个关键步骤：

- **初始化PID参数**：在程序开始时，根据控制器要求初始化P、I、D参数。
- **读取系统输入和状态**：从传感器或其他输入设备获取必要的系统状态信息。
- **计算偏差**：偏差是期望设定点和实际输出之间的差异，这是PID算法的输入之一。
- **更新PID控制器输出**：根据计算得到的偏差、以及P、I、D参数更新控制器输出。
- **发送控制指令**：将计算得到的输出值发送到执行器，如电机或阀门，以调整系统状态。

示例代码块（伪代码）：

# PID 控制器的简单实现
class PIDController:
    def __init__(self, kp, ki, kd, set_point):
        self.kp = kp  # 比例增益
        self.ki = ki  # 积分增益
        self.kd = kd  # 微分增益
        self.set_point = set_point  # 设定点
        self.previous_error = 0
        self.integral = 0
        # 其他初始化代码

    def update(self, current_value):
        error = self.set_point - current_value
        self.integral += error
        derivative = error - self.previous_error
        output = (self.kp * error) + (self.ki * self.integral) + (self.kd * derivative)
        self.previous_error = error
        return output

# 创建PID实例，并调整到实际应用环境
pid = PIDController(kp=1.0, ki=0.1, kd=0.05, set_point=desired_value)
control_signal = pid.update(measured_value)

### 3.3.2 模拟软件在PID优化中的应用

模拟软件是测试和优化PID控制策略的有效工具，它允许工程师在不干扰实际系统的情况下，调整PID参数和测试控制系统性能。

- **模拟软件环境**：现代模拟软件支持复杂控制系统的设计和仿真。它们提供了灵活的建模环境、丰富的工具库和直观的用户界面。

- **参数调整**：在模拟环境中，可以方便地调整PID参数并观察系统的响应。通过反复模拟，可以找到最佳的PID参数。

- **实验和测试**：模拟软件能够在多种工况和故障情况下测试PID控制器的性能，提供了安全且成本效益高的测试平台。

模拟软件工具如MATLAB/Simulink和Modelica都是进行PID控制策略开发和优化的有力工具。通过使用这些工具，工程师可以直观地看到系统对参数变化的响应，分析系统的稳定性和动态特性，从而实现高效、精确的系统优化。

通过上述讨论，可以了解到PID控制策略在现代控制系统中扮演着至关重要的角色。通过理解和应用先进PID控制算法、优化技术和模拟工具，控制系统工程师可以显著提升系统性能，优化控制效果，以适应各种复杂的应用场景。

# 4. PID控制系统的调试与性能评估

在设计和实施PID控制系统之后，重要的一步是对其进行调试和性能评估。这是一个确认系统是否按预期工作，以及是否需要进一步调整的过程。本章节将详细介绍系统调试的步骤、性能评估标准以及如何通过实际案例分析进行故障排除。

## 4.1 系统调试步骤与方法

系统调试是对控制系统进行测试和修改，以确保其在实际工作条件下的性能符合设计要求。调试过程通常涉及对控制回路的开环和闭环测试。

### 4.1.1 开环和闭环调试

开环调试是指在未形成闭环的情况下，对控制器进行调试。在这个阶段，控制器的输出直接影响执行机构，但不通过过程变量反馈回来。开环调试的目的是检查控制器的逻辑和硬件部分是否正确工作。

flowchart LR
    A[开环调试] --> B[确认控制器逻辑]
    B --> C[硬件功能检查]
    C --> D[调整控制器参数]
    D --> E[转至闭环调试]

闭环调试涉及到整个控制回路。在这个阶段，控制器会根据反馈信号调节其输出，以达到设定的目标值。闭环调试的主要目的是确保系统稳定，并且满足性能规格。

flowchart LR
    F[闭环调试] --> G[设定目标值]
    G --> H[检查系统响应]
    H --> I[调整PID参数]
    I --> J[系统稳定性分析]
    J --> K[性能评估]
    K --> L[结束调试]

### 4.1.2 阶跃响应测试与分析

阶跃响应测试是一种常用的调试手段，它通过将系统设定点从一个稳定值瞬间改变到另一个稳定值，观察系统输出的反应。通过分析阶跃响应曲线，可以评估系统的动态性能指标，如上升时间、峰值时间和稳态误差。

graph LR
    A[阶跃响应测试] --> B[上升时间分析]
    B --> C[峰值时间分析]
    C --> D[稳态误差分析]
    D --> E[性能指标记录]
    E --> F[系统调整和再测试]

## 4.2 PID控制器的性能评估标准

性能评估是确保PID控制达到预期效果的关键。性能评估标准通常包括对稳态误差和稳定性分析，以及对动态响应指标的测量与评估。

### 4.2.1 稳态误差与稳定性分析

稳态误差是指在系统达到稳态后，输出和设定目标值之间的差异。一个良好设计的PID控制器应当能够最小化稳态误差。

e_{ss} = \lim_{t \to \infty} (r(t) - y(t))

其中，`e_ss` 是稳态误差，`r(t)` 是设定值，`y(t)` 是输出值。

系统稳定性是指系统在受到干扰或变化时，能够返回到其稳定状态的能力。稳定性分析可以通过劳斯稳定判据或根轨迹方法来进行。

### 4.2.2 动态响应指标的测量与评估

动态响应指标包括上升时间、峰值时间、超调量和调整时间等。这些指标可以帮助我们了解系统对输入变化的响应速度和质量。

| 指标 | 定义 |
| --- | --- |
| 上升时间 | 从系统响应开始到达最终稳定值的90%所需的时间 |
| 峰值时间 | 系统响应达到峰值所需的时间 |
| 超调量 | 系统响应超过最终稳定值的最大量 |
| 调整时间 | 系统响应进入并保持在最终稳定值的某个小范围内所需的时间 |

通过对这些动态响应指标的测量与评估，工程师可以判断PID控制器的性能，以及是否需要进一步的优化。

## 4.3 实际案例分析与故障排除

实际应用中的PID控制系统的调试和性能评估往往比理论分析更为复杂。这里将通过几个实际案例来分析如何进行故障排除。

### 4.3.1 成功案例分享

案例1: 温度控制系统优化

在某工业炉温度控制系统中，通过使用Ziegler-Nichols方法对PID参数进行初次设定，随后结合阶跃响应测试调整PID参数，最终实现了一个快速响应且无超调的温度控制过程。详细过程和调整结果如下：

| 参数 | 初次设定值 | 优化后值 |
| --- | --- | --- |
| Kp | 1.2 | 1.4 |
| Ki | 0.02 | 0.025 |
| Kd | 0.01 | 0.005 |

通过对比，发现优化后的系统响应更快，且稳态误差更小。

### 4.3.2 常见问题诊断与解决方法

问题1: 控制系统的持续振荡

振荡问题是PID控制中最常见的一种故障。振荡可能是由于PID参数不适当导致的。解决方法包括：

- 降低Kp，减少控制器的响应力度。
- 增加Ki的微分时间Td，提高系统的阻尼比。
- 检查并调整Kd，确保微分项对系统起到稳定作用。

代码块用于展示如何通过软件模拟来诊断和调整PID参数：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# 系统动态方程
def pid_system(y, t, Kp, Ki, Kd, setpoint):
    u = Kp * (setpoint - y) - Kd * y_dot - Ki * y_integral
    y_dot = u
    y_integral = y_integral + y * dt
    return y_dot

# 初始条件和参数
y0 = [0]
setpoint = 1.0
dt = 0.01
time = np.arange(0, 5, dt)

# 参数调整前
params_before = {'Kp': 2.0, 'Ki': 0.05, 'Kd': 0.2}
solution_before = odeint(pid_system, y0, time, args=(params_before['Kp'], params_before['Ki'], params_before['Kd'], setpoint))

# 参数调整后
params_after = {'Kp': 1.5, 'Ki': 0.05, 'Kd': 0.3}
solution_after = odeint(pid_system, y0, time, args=(params_after['Kp'], params_after['Ki'], params_after['Kd'], setpoint))

# 绘图对比
plt.plot(time, solution_before, label='调整前')
plt.plot(time, solution_after, label='调整后')
plt.axhline(y=setpoint, color='r', linestyle='--', label='设定值')
plt.legend()
plt.xlabel('时间')
plt.ylabel('响应')
plt.title('PID参数调整前后对比')
plt.show()

通过这样的模拟，可以观察到在调整PID参数后，系统振荡明显减少，响应曲线更加平滑。

在本章节的介绍中，详细解析了PID控制系统调试的步骤和性能评估的方法。此外，通过实际案例分析展示了如何解决实际问题，并借助代码示例对调整过程进行了模拟。接下来的章节将探索PID控制的未来趋势和研究方向，包括智能控制与PID结合的前景，以及多变量PID控制系统和分布式PID控制网络的发展。

# 5. PID控制的未来趋势与研究方向

随着工业自动化和智能化的发展，PID控制作为一种成熟的控制方法，其在许多领域仍然占据着重要的地位。然而，伴随着技术进步和控制理论的革新，PID控制技术也在不断适应新的需求，展现出新的发展趋势。本章将深入探讨PID控制的未来趋势、工业应用扩展以及控制系统研究的建议。

## 5.1 智能控制与PID的结合前景

### 5.1.1 机器学习在PID控制中的应用

机器学习尤其是深度学习技术的进步，为PID控制提供了新的优化途径。在实际应用中，机器学习算法可以分析大量的历史控制数据，学习控制器在不同工况下的最佳行为。通过这种方式，机器学习算法可以辅助PID控制器动态调整其参数，以适应变化的环境和工作条件。

例如，可以设计一种基于神经网络的PID控制器，其中神经网络的作用是预测系统的未来行为并给出最佳的控制策略。实现这种控制器通常需要以下步骤：

1. 数据收集：收集系统在不同工况下的输入输出数据。
2. 网络训练：使用收集的数据对神经网络进行训练，使其能够准确预测系统的动态行为。
3. 控制策略优化：利用神经网络预测结果，优化PID控制器的参数调整规则。
4. 在线调整：在控制器实际运行过程中，根据实时数据不断调整神经网络权重，以提高控制精度。

### 5.1.2 神经网络PID控制器的发展

神经网络PID控制器利用神经网络强大的非线性映射能力和学习能力，可以实现对传统PID控制器的优化。控制器结合了神经网络的预测能力和PID控制的简单易行特点，适合处理那些非线性、时变、复杂系统的控制问题。

这类控制器的典型结构包括一个或多个神经网络，它们与传统的PID控制器并行工作，以实现以下功能：

- 系统建模：神经网络可以被训练用来模拟系统的动态行为。
- 参数自适应：根据系统模型的实时预测结果，动态调整PID参数。
- 非线性控制：处理那些传统PID控制器难以应对的非线性控制问题。

## 5.2 PID控制的工业应用与扩展

### 5.2.1 多变量PID控制系统

在许多工业应用中，系统的控制变量往往不止一个。多变量PID控制系统可以同时控制多个输入和输出变量，从而更精确地控制复杂过程。多变量PID控制器通常利用解耦技术和解耦矩阵，确保各个控制回路之间的相互作用最小化。

设计多变量PID控制器通常需要考虑以下方面：

- 控制对象的建模：明确系统中各个变量之间的关系，建立精确的多变量控制模型。
- 解耦策略：设计有效的解耦策略，降低或消除各个控制回路之间的相互干扰。
- 参数调整：针对多变量系统特性进行PID参数的精细调整，以达到期望的控制效果。

### 5.2.2 分布式PID控制网络

随着工厂自动化和信息化水平的提高，分布式控制网络成为工业控制的新趋势。分布式PID控制网络能够有效集成多个控制节点，实现控制系统的集中管理与分散执行。这种网络架构具有高度的灵活性和可靠性，适合复杂和大规模的控制系统。

分布式PID控制网络的关键特点包括：

- 控制节点分布：将控制任务分散到各个控制节点，减轻主控制器负担。
- 数据通信：通过网络实现节点间的通信，保证控制命令的准确传递和执行。
- 集成监控：建立集中的监控系统，实现对整个控制网络状态的实时监控和管理。

## 5.3 持续学习与控制系统研究的建议

### 5.3.1 学术交流与合作的重要性

在控制系统的研究与开发中，跨学科合作和学术交流对于推动技术创新具有不可忽视的作用。通过学术交流，研究人员可以分享最新研究成果，交流经验，共同解决控制领域面临的挑战。

为了促进学术交流，以下几点建议值得考虑：

- 组织研讨会和论坛：定期组织研讨会和论坛，邀请领域内的专家和学者进行深入讨论。
- 发表联合研究论文：鼓励合作研究，发表高水平的联合研究论文，提升研究成果的影响力。
- 促进企业与学术界的合作：鼓励和促进企业与学术界的合作，将理论研究转化为实际应用。

### 5.3.2 未来研究与技术发展的展望

随着科技的不断进步，未来的控制系统将更加智能、高效和可靠。在研究方向上，以下几个方面值得关注：

- 人工智能与控制系统的融合：探索人工智能技术，尤其是深度学习和强化学习在控制系统中的应用。
- 自适应和自组织控制理论的研究：研究能够自适应环境变化和系统参数变化的新型控制策略。
- 量子控制理论的探索：随着量子计算的发展，研究量子控制理论，为未来的控制系统提供新的理论基础。

通过上述的深入探讨，我们可以看到PID控制技术在不断演化和优化，正逐步迈向更加智能化和自动化的未来。无论是从理论研究到实际应用，还是从单一的控制策略到综合的控制系统解决方案，PID控制都有着广泛的发展空间和潜力。