【LightGBM实战案例集】：真实世界问题的解决方案

# 1. LightGBM模型简介与理论基础

在机器学习领域，提升模型的性能始终是研究的核心目标之一。LightGBM作为一个高效的分布式梯度提升框架，在各类机器学习竞赛和实际应用中被广泛应用，它的出现为大数据环境下的模型训练提供了强有力的支持。本章我们将初步介绍LightGBM模型，探索其理论基础，为后续章节深入了解算法原理及应用实战打下坚实基础。

## 1.1 LightGBM简介

LightGBM是由微软开发的基于梯度提升框架的决策树算法。它在传统的梯度提升树（Gradient Boosting Tree, GBT）的基础上进行了多项优化，显著提高了计算效率和内存消耗。LightGBM特别适合于处理大规模数据集，这得益于其对数据的优化预处理和更快的训练速度。

## 1.2 理论基础

LightGBM建立在梯度提升机制之上，即通过迭代方式组合多棵弱学习器（本例中为决策树），以达到提升模型预测精度的目的。理论上来讲，每一轮迭代都试图减小损失函数，直至收敛。LightGBM通过在每一步选择最佳特征并创建分裂点来构建树，从而最小化损失函数。此外，LightGBM采用了基于直方图的算法来提升效率，其原理是对连续特征值进行离散化处理，以减少计算复杂度。

## 1.3 应用场景

LightGBM的高效性和良好的泛化能力使其成为解决回归、分类等多种机器学习问题的理想选择。尤其在金融信贷风险评估、零售销售预测、医疗诊断等领域，LightGBM展现出了巨大的应用潜力。接下来的章节中，我们将深入探讨LightGBM的算法原理，并通过具体案例展示其在实际问题中的应用。

# 2. ```
# 第二章：LightGBM算法原理深入

## 2.1 LightGBM的梯度提升决策树

### 2.1.1 梯度提升框架的基本概念

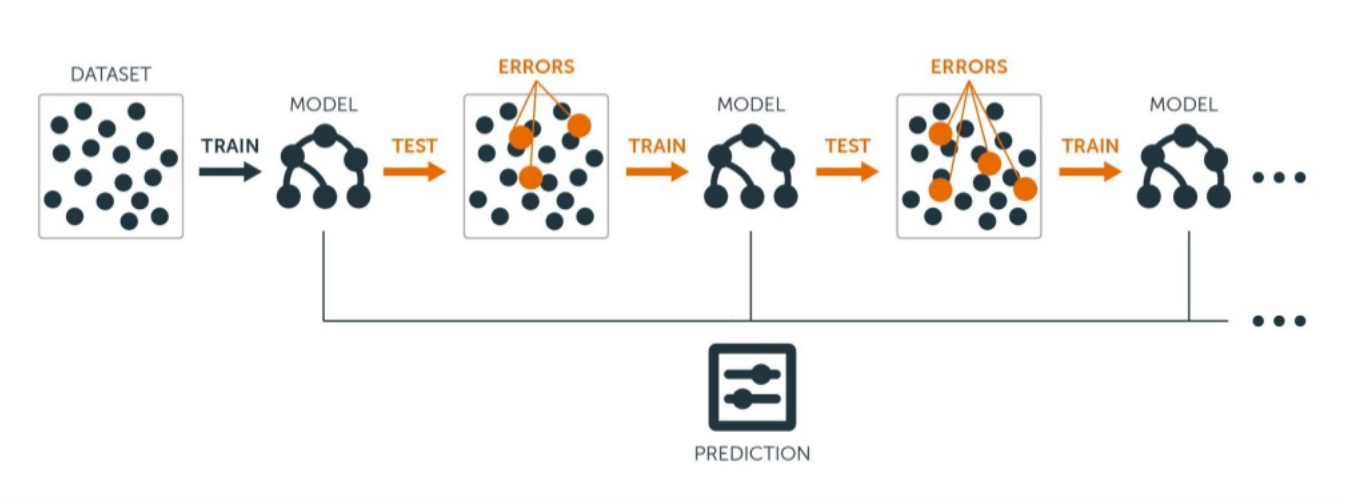
梯度提升（Gradient Boosting）是一种强大的集成学习方法，用于回归和分类问题。它通过连续地添加弱学习器来减少损失函数，而这些弱学习器通常是决策树。在每一轮迭代中，新加入的树都尝试减少上一轮树预测的残差。在LightGBM中，使用了梯度提升框架来逐步构建强学习器。

梯度提升树的核心思想是通过组合多个弱分类器来构造一个强分类器。每次迭代都会增加一棵树，用于纠正前面所有树的预测误差。具体来说，如果在第t轮之后，模型的预测为F_t(x)，那么下一轮模型的预测F_{t+1}(x)可以表示为：

F_{t+1}(x) = F_t(x) + h(x)

这里，`h(x)`是第t+1轮要添加的弱学习器，通常是决策树。在LightGBM中，每棵树都是在残差的基础上训练的，目的是减少上一轮模型的预测误差。

### 2.1.2 LightGBM中的树模型构建

在LightGBM中，构建树模型的步骤通常包括以下几个环节：

1. **初始化模型**：设置初始模型为一个常数，通常是训练集标签的均值。
2. **迭代构建树**：对于每一轮迭代，都尝试增加一棵树来减少损失函数。
3. **选择最佳分割点**：在LightGBM中，通常使用直方图算法来选择最佳的分割点，这将在下一小节详细介绍。
4. **更新残差**：计算新的残差，即真实标签与当前模型预测值的差异。
5. **更新模型**：将新树的预测值添加到模型中。

在构建决策树的过程中，LightGBM采用了基于直方图的算法，它通过对特征值进行分桶来减少内存使用和加速计算。直方图算法将在后续的小节中详细讨论。

### *.*.*.* 基于直方图的算法

LightGBM使用基于直方图的算法来优化决策树的训练过程。直方图算法将连续的特征值分割成离散的桶（bins），这样可以将特征空间的维度降低到桶的数量级，大大减少了需要处理的数据量。

这个方法的核心在于它将特征值的计算转变为桶索引的计算，因此可以利用缓存的局部性原理和向量化操作，提高计算效率。此外，直方图算法还支持高效的并行计算和GPU加速，进一步提升了训练速度。

## 2.2 LightGBM的优化策略

### 2.2.1 直方图算法的原理与优势

直方图算法在LightGBM中的应用不仅仅局限于提升训练速度，它还能够改善模型的内存使用效率和计算精度。具体来说，直方图算法的原理和优势包括：

- **减少计算量**：通过将特征值分割成离散的桶，将连续的特征值划分成有限数量的区间，减少了分割点搜索的数量。
- **提升内存效率**：使用整数索引代替浮点数特征值，减少了内存的使用。
- **加快训练速度**：减少了需要比较的候选分割点数量，减少了模型训练的时间。
- **支持并行计算**：由于特征值已经被分桶，因此可以在多个桶上并行计算分割点。
- **GPU加速**：直方图算法可以很好地与GPU并行加速技术相结合，进一步提升计算速度。

### 2.2.2 带宽优化和样本采样方法

在LightGBM中，带宽优化和样本采样是两个重要的策略，用于进一步提升模型的训练效率和泛化能力。

- **带宽优化**：通过调整直方图算法中的桶宽度来控制模型的复杂度。较小的桶宽度可以得到更精细的特征分割，从而提高模型的准确度，但也会增加计算的复杂度和内存消耗。反之，较大的桶宽度可以减少计算资源的使用，但可能会牺牲一定的模型精度。
- **样本采样**：在每一轮迭代中，LightGBM可以对训练数据进行采样以构建新的树。这不仅减少了每一轮树构建的计算量，还可以通过子样本的不同组合来防止过拟合。常见的采样方法包括随机采样、基于梯度的采样等。

### 2.2.3 系统和硬件加速技术

为了进一步提升训练速度，LightGBM采用了多种系统和硬件加速技术，使得模型可以利用现代计算机的多核CPU和GPU进行加速。

- **CPU多线程加速**：通过并行计算来同时处理多个任务。LightGBM在构建决策树时，可以同时处理多个特征的候选分割点的计算。
- **GPU加速**：针对特定的计算任务，如直方图算法的构建和更新，LightGBM可以利用GPU的强大并行处理能力来显著提高训练速度。
- **分布式计算**：对于大规模数据集，LightGBM支持在多个计算节点上分布式地训练模型，从而充分利用集群资源。

## 2.3 LightGBM的模型评估与选择

### 2.3.1 交叉验证和超参数调优

为了评估模型的泛化能力，并选择最优的超参数设置，LightGBM提供了交叉验证的方法。交叉验证通常包括K折交叉验证，它将数据集分成K个大小相等的子集，轮流使用其中的K-1个子集进行训练，剩下的1个子集用于测试。通过这种方式，可以更加准确地估计模型在未知数据上的表现。

import lightgbm as lgb
import numpy as np
from sklearn.model_selection import KFold

# 生成一些模拟数据
X, y = np.random.rand(1000, 10), np.random.randint(2, size=1000)
kf = KFold(n_splits=5)

for train_index, test_index in kf.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    dtrain = lgb.Dataset(X_train, label=y_train)
    dtest = lgb.Dataset(X_test, label=y_test, reference=dtrain)

    params = {
        'objective': 'binary',
        'metric': 'binary_logloss'
    }

    gbm = lgb.train(params,
                    train_set=dtrain,
                    num_boost_round=20,
                    valid_sets=[dtrain, dtest],
                    early_stopping_rounds=5)

上述代码展示了如何使用LightGBM进行交叉验证。`KFold`类用于生成训练和测试的索引，`lgb.train`函数则根据这些索引训练模型，并在每一轮迭代后验证模型的性能。

### 2.3.2 模型复杂度和泛化能力分析

在选择最终的LightGBM模型时，除了考虑模型的准确度之外，还应该关注模型的复杂度和泛化能力。过于复杂的模型可能会过拟合，即在训练数据上表现很好，但在未知数据上泛化能力较差。

- **模型复杂度**：可以通过树的数量、树的深度、叶子节点的数量等指标来衡量。
- **正则化技术**：为了防止过拟合，可以采用正则化技术，如限制树的深度、设置叶子节点的最小样本数、应用L1和L2正则化项等。
- **特征选择**：通过特征重要性评估和选择，减少不相关特征的干扰，提高模型的泛化能力。

# 示例代码：正则化技术在LightGBM中的应用
params = {
    'objective': 'binary',
    'metric': 'binary_logloss',
    'max_depth': 10,  # 树的最大深度
    'min_data_in_leaf': 10,  # 叶子节点的最小样本数
    'lambda_l1': 0.