【计数器革命】：扭环形计数器提高系统效率的策略（高效时序管理技巧）


# 摘要
本文综合探讨了扭环形计数器的原理、应用和优化方法，并深入分析了其在不同领域的具体应用。通过理解扭环形计数器的工作机制和性能调优策略，我们能够评估其在系统效率和时序管理中的重要性。文章还讨论了系统效率的理论基础，包括时间复杂度与空间复杂度的分析及优化案例，以及高效时序管理的理论框架。此外，文章展望了扭环形计数器未来的发展方向，包括技术创新的驱动力和对系统效率极限的挑战与机遇。

# 关键字
扭环形计数器；系统效率；时序管理；性能调优；实时系统；高性能计算

参考资源链接：[扭环形计数器：同步二进制与N进制逻辑详解](https://wenku.csdn.net/doc/5u1ne7av12?spm=1055.2635.3001.10343)
# 1. 扭环形计数器的原理与应用

## 1.1 扭环形计数器简介

扭环形计数器（Twisted Ring Counter）是一种数字电路设备，广泛应用于计时、计数以及序列生成等领域。它的核心在于利用一系列的触发器，以特定的顺序进行状态变换，形成循环的计数过程。

## 1.2 原理分析

扭环形计数器的运作原理基于移位寄存器。每个触发器（通常为D触发器）都拥有一个输入端和一个输出端，通过环形连接形成一个闭合的环路。状态的切换通常由一个时钟信号触发，当信号到来时，每个触发器的输出状态将被其右侧的触发器读取并存储。

## 1.3 应用场景

在实际应用中，扭环形计数器可以用于构建数字分频器、产生序列代码、以及实现简单的状态机。由于其简洁的结构，它在集成度要求高和成本有限的场合中特别受到青睐。

以上章节内容为扭环形计数器的基础介绍，简洁清晰地说明了其基本概念、工作原理以及在不同场景中的应用情况。在后续章节中，我们将深入探讨系统效率的理论基础，并详细分析扭环形计数器在实现与优化、不同领域的应用以及未来技术挑战等课题。

# 2. 系统效率的理论基础

### 2.1 系统效率的重要性

系统效率是衡量系统在特定任务上完成工作速度和质量的重要指标。它直接关联到资源利用率、处理能力、响应时间以及最终的系统性能。

#### 2.1.1 定义与衡量标准

系统效率的定义可以从多个维度来解读，但其核心都是对资源消耗和产出之间的比例关系进行量化。衡量标准包括但不限于：

- **时间效率**：处理特定任务所需的总时间，包括响应时间、处理时间等。
- **资源效率**：对物理资源（如CPU、内存）、能源消耗以及成本的有效利用。
- **吞吐量**：单位时间内系统可以处理的最大任务量。
- **可靠性和稳定性**：系统持续稳定运行的能力，减少故障和停机时间。

#### 2.1.2 效率与性能的关系

效率和性能之间存在密切关系，但它们并非总是等同。性能通常指的是系统达到预期目标的能力，而效率则更多关注如何以最小的成本达到这个目标。提高效率可以提升性能，但优化性能往往需要从多个角度考虑，包括算法优化、资源调度策略以及硬件升级等。

### 2.2 时间复杂度与空间复杂度

在算法设计和系统优化中，时间复杂度和空间复杂度是两个基础概念，它们决定了算法的可扩展性和资源占用情况。

#### 2.2.1 算法的时间复杂度分析

时间复杂度用于量化算法执行时间随输入数据规模增长的变化趋势。常见的复杂度类别包括：

- **常数时间**：O(1)
- **对数时间**：O(log n)
- **线性时间**：O(n)
- **线性对数时间**：O(n log n)
- **平方时间**：O(n^2)
- **指数时间**：O(2^n)

不同的算法根据其时间复杂度在执行效率上差异巨大，选择合适的算法对于提升系统效率至关重要。

#### 2.2.2 算法的空间复杂度分析

空间复杂度衡量的是算法执行过程中所需的最大额外空间。它与时间复杂度类似，是评估算法性能的重要指标。例如，快速排序的时间复杂度为O(n log n)，但如果在空间复杂度上优化，可以实现原地快速排序，其空间复杂度降为O(log n)。

#### 2.2.3 优化案例：寻找平衡点

在优化时间复杂度和空间复杂度时，往往需要在二者之间寻找平衡点。一个经典的例子是使用哈希表进行数据存储和检索。哈希表具有平均时间复杂度O(1)的查询速度，但其空间复杂度取决于负载因子和哈希函数的设计。优化负载因子可以平衡空间和时间的开销。

### 2.3 高效时序管理的理论框架

时序管理是系统中非常重要的概念，它涉及到系统的响应性和实时性。优秀的时序管理可以提高系统的效率，提升服务质量。

#### 2.3.1 时序分析的基本概念

时序分析主要研究系统在执行任务时的时间分布，包括任务的调度、执行顺序和时间间隔。通过时序分析，可以识别出系统中的瓶颈和延迟，为优化提供依据。

#### 2.3.2 时序优化的原则和方法

时序优化的原则包括：

- **最小化延迟**：减少任务响应和执行所需时间。
- **负载均衡**：合理分配系统资源，避免某些部分过载。
- **预测和调度**：通过预测任务行为，提前做好调度准备。

方法上，包括：

- **任务优先级管理**：确保重要或紧急的任务优先执行。
- **动态调度策略**：根据实时数据调整任务执行计划。
- **反馈控制**：通过反馈机制调整执行策略，以适应变化。

### 2.3.3 时序管理的实际应用

在实际应用中，时序管理可以优化任务执行顺序，降低资源竞争。例如，在嵌入式系统中，通过时序分析和优化，能够保证关键任务在严格的时间约束内完成，从而提升整体系统性能。

通过本章节的介绍，理解了系统效率的重要性，并掌握了时间复杂度与空间复杂度的基础知识。此外，高效时序管理的理论框架为后续章节中扭环形计数器的实现与优化提供了理论支持。

# 3. 扭环形计数器的实现与优化

扭环形计数器是计算机科学中一个重要的概念，它在硬件层面实现了高效的计数功能，尤其在需要高速计数和环形数据结构的场景中表现出色。为了深入理解扭环形计数器的工作原理及其优化策略，本章将详细探讨扭环形计数器的内部工作机制，以及在实际应用中如何进行性能调优。

## 3.1 扭环形计数器的工作机制

### 3.1.1 计数器的结构和组成

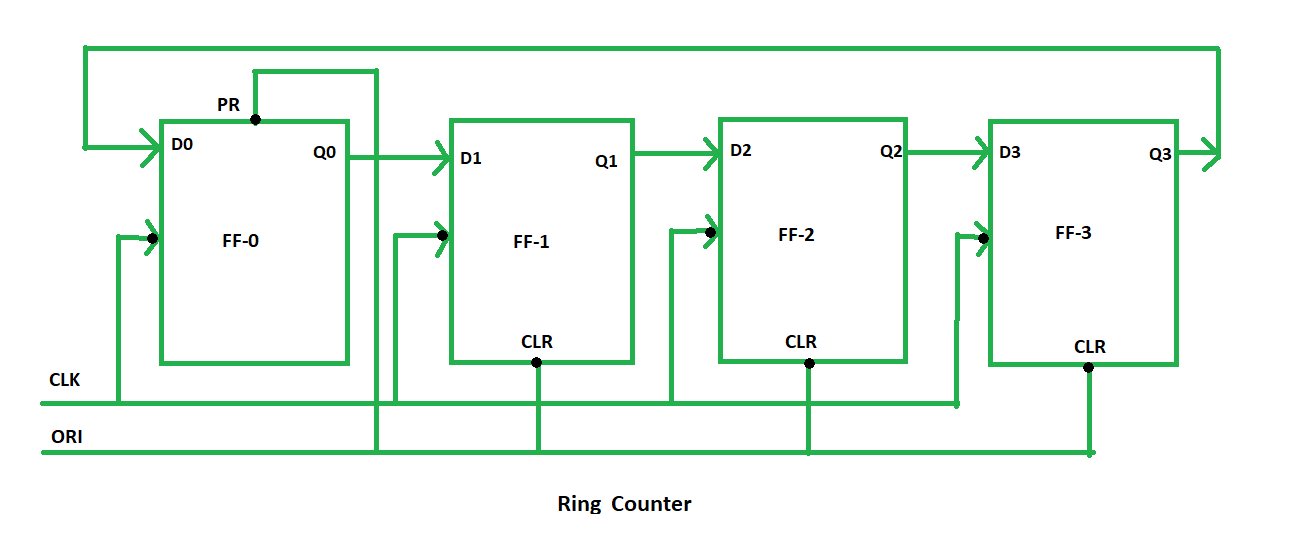
扭环形计数器（也称为约翰逊计数器）是由一系列的触发器（Flip-Flops）构成的，它们以特殊的方式互相连接。在最简单的情况下，一个N位的扭环形计数器由N个D触发器组成，触发器的输出连接到下一个触发器的输入。第一级触发器的输出通过一个非门（NOT gate）后送回到最后一级触发器的输入。这样就形成了一个“环”。

为了展示扭环形计数器的工作原理，下面是它的一个基本结构示意图：

flowchart LR
    A[触发器D0] -->|非| B[触发器D1]
    B --> C[触发器D2]
    C -->|...| D[...]
    D --> E[触发器Dn]
    E -->|非| A

该图展示了触发器之间的连接方式，通过这种方式可以实现计数器的循环特性。

### 3.1.2 动态进位与循环特性

扭环形计数器的一个显著特点是它具有动态进位和循环计数的能力。在扭环形计数器中，一个触发器的输出状态会影响另一个触发器的输入。这允许计数器在一个周期结束后，能够快速回转并重新开始计数。

一个四位的扭环形计数器可以展示其循环特性，其状态转移表如下：

| 当前状态 | 下一个状态 |
|---------|---------|
| 0000 | 1000 |
| 1000 | 1100 |
| 1100 | 1110 |
| 1110 | 1111 |
| 1111 | 0111 |
| ... | ... |

通过观察状态转移表，可以发现该计数器从全0状态开始，通过动态进位达到全1状态，然后快速回转至1000状态，并继续进行循环计数。

### 3.1.3 计数器的代码实现

为了更好地理解扭环形计数器的工作方式，我们可以通过编写一个简单的模拟代码来实现一个四位的扭环形计数器。下面是一个使用Verilog语言实现扭环形计数器的代码示例：

module ring_counter(
    input clk,        // 时钟信号
    input reset,      // 异步复位信号
    output reg [3:0] out // 计数器输出
);

// 异步复位和时钟边沿触发
always @(posedge clk or posedge reset) begin
    if (reset) begin
        out <= 4'b0000; // 异步复位到0000状态
    end else begin
        out <= {out[2:0], ~out[3]}; // 通过循环右移实现计数
    end
end

endmodule

在这段代码中，我们定义了一个名为`ring_counter`的模块，它有一