JavaScript算法精髓：动态规划与贪心算法的15个实战案例

# 1. 动态规划与贪心算法概述

在探索高效算法的世界中，动态规划（Dynamic Programming，简称DP）和贪心算法（Greedy Algorithm）是两种解决优化问题的基石。动态规划依赖于将复杂问题分解为更小子问题的解决方案，并存储这些子问题的解以避免重复计算，从而实现问题的高效求解。而贪心算法则通过在每一步选择中都采取在当前状态下最好或最优的选择，从而希望导致结果是最好或最优的算法。虽然它们在解决优化问题时都极具威力，但每种方法适用的场景和限制都有所不同。了解这些基础理论，对于解决实际中的问题至关重要。接下来的章节将详细阐述这两种算法的理论基础、应用实例和解题技巧，帮助你全面掌握它们的精髓。

# 2. 动态规划理论与实践

动态规划是解决优化问题的一种方法，特别是那些可以分解为相对简单的子问题的问题。在这一章中，我们将深入探讨动态规划的理论基础、经典问题、解题步骤，并通过实践案例加深理解。

## 2.1 动态规划基础

### 2.1.1 动态规划的定义与特点

动态规划（Dynamic Programming，DP）是一种算法思想，用于解决具有重叠子问题和最优子结构性质的复杂问题。它通常用于求解最优化问题，即寻找问题的一个或多个最优解。动态规划的特点包括：

- **重叠子问题**：在计算过程中，许多子问题被多次计算。动态规划通过存储这些子问题的解（通常存储在一个数组中），避免了重复计算。
- **最优子结构**：一个问题的最优解包含其子问题的最优解。
- **无后效性**：子问题的解只依赖于子问题本身的输入，而不依赖于整个问题的其他部分。

### 2.1.2 动态规划问题的结构分析

动态规划问题通常可以通过以下步骤进行结构化分析：

1. **确定状态**：定义子问题的解，通常是通过一个或多个变量来描述。
2. **状态转移方程**：确定如何通过子问题的解推导出原问题的解。
3. **边界条件**：确定子问题解的初始条件。
4. **最优子结构**：证明问题的最优解中包含了子问题的最优解。
5. **重叠子问题**：确保动态规划方法是高效的，通过识别问题中的重叠子问题。

## 2.2 动态规划的经典问题

### 2.2.1 斐波那契数列问题

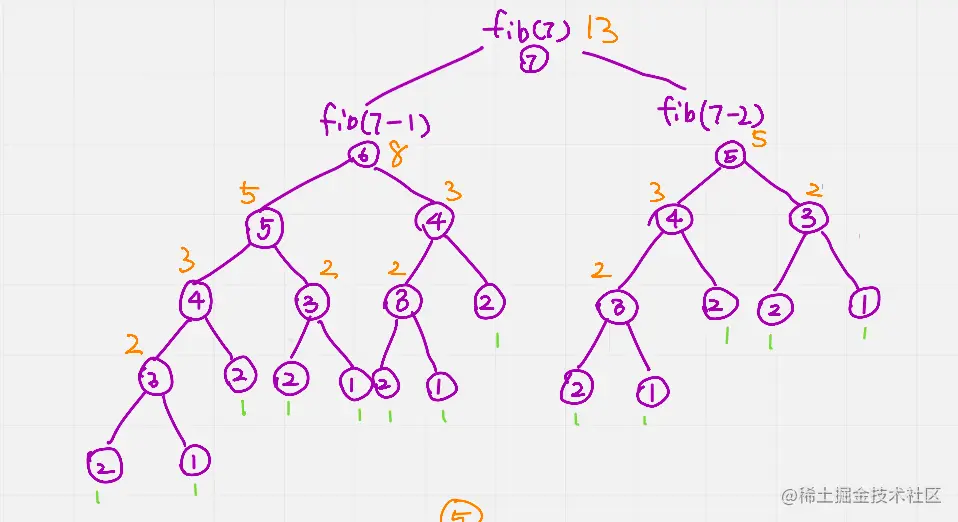
斐波那契数列是动态规划的经典入门案例。数列中每个数字是前两个数字的和，通常定义为 `F(0)=0`, `F(1)=1`，对于 `n>1`，`F(n)=F(n-1)+F(n-2)`。通过动态规划求解斐波那契数列的第n项可以通过以下步骤实现：

1. **定义状态**：`dp[i]` 表示斐波那契数列的第 `i` 项。
2. **状态转移方程**：`dp[i] = dp[i-1] + dp[i-2]`。
3. **边界条件**：`dp[0] = 0`, `dp[1] = 1`。
4. **计算顺序**：从 `2` 开始递增计算到 `n`。

def fibonacci(n):
    if n <= 1:
        return n
    dp = [0] * (n+1)
    dp[1] = 1
    for i in range(2, n+1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

### 2.2.2 爬楼梯问题

假设你正在爬楼梯，需要 n 步才能到达楼顶。每次你可以爬 1 或 2 个台阶。问题在于有多少种不同的方法可以爬到楼顶。此问题同样具有最优子结构和重叠子问题的性质，可以通过动态规划解决。

1. **定义状态**：`dp[i]` 表示到达第 `i` 阶台阶的方法数。
2. **状态转移方程**：`dp[i] = dp[i-1] + dp[i-2]`。
3. **边界条件**：`dp[1] = 1`, `dp[2] = 2`。
4. **计算顺序**：从 `3` 开始递增计算到 `n`。

def climb_stairs(n):
    if n <= 2:
        return n
    dp = [0] * (n+1)
    dp[1], dp[2] = 1, 2
    for i in range(3, n+1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

### 2.2.3 最长公共子序列问题

最长公共子序列（Longest Common Subsequence，LCS）是另一个典型的动态规划问题。给定两个序列，求它们的最长公共子序列的长度。

1. **定义状态**：`dp[i][j]` 表示序列 `X[1..i]` 和 `Y[1..j]` 的最长公共子序列的长度。
2. **状态转移方程**：如果 `X[i] == Y[j]`，则 `dp[i][j] = dp[i-1][j-1] + 1`；否则，`dp[i][j] = max(dp[i-1][j], dp[i][j-1])`。
3. **边界条件**：`dp[i][0] = 0` 和 `dp[0][j] = 0` 对所有的 `i, j` 成立。
4. **计算顺序**：递增计算 `i` 和 `j`，通常可以嵌套循环遍历两个序列。

def lcs(X, Y):
    m = len(X)
    n = len(Y)
    L = [[0] * (n+1) for i in range(m+1)]
    for i in range(m+1):
        for j in range(n+1):
            if i == 0 or j == 0:
                L[i][j] = 0
            elif X[i-1] == Y[j-1]:
                L[i][j] = L[i-1][j-1] + 1
            else:
                L[i][j] = max(L[i-1][j], L[i][j-1])
    return L[m][n]

## 2.3 动态规划问题的解题步骤

### 2.3.1 状态定义与状态转移方程

在动态规划中，正确地定义状态和状态转移方程是解题的关键。状态通常是一个或多个变量的组合，它能够代表问题的某个阶段或子问题的解。状态转移方程描述了如何从一个状态转移到另一个状态。

### 2.3.2 边界条件与初始状态

边界条件是状态定义的一部分，它定义了问题的起始点。在上面的例子中，`dp[0] = 0` 和 `dp[1] = 1` 就是边界条件。初始状态通常是动态规划表格中的第一行或第一列。

### 2.3.3 代码实现与优化策略

代码实现是将算法思路转化为程序的过程。在编写代码时，需要考虑如下因素：

- **空间优化**：通过滚动数组等技术减少空间复杂度。
- **时间优化**：避免不必要的计算，例如利用已有的中间结果。
- **逻辑优化**：代码清晰、高效，并且易于理解。

动态规划的问题通常可以通过表格的方式可视化，以 `dp` 表示的表格用于存储子问题的解，有助于理解问题的结构和解题流程。

接下来，我们将继续探讨贪心算法的理论与实践，了解这种与动态规划有着密切联系，但解决问题的方式截然不同的算法思想。

# 3. 贪心算法理论与实践

## 3.1 贪心算法基础

### 3.1.1 贪心算法的定义与原则

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。贪心算法的核心在于，对于当前步骤，它总是做出在某种意义上的最优选择。不过，贪心算法并不是对所有问题都能得到最优解，它适用于具有“贪心选择性质”的问题。所谓贪心选择性质，是指局部最优解能决定全局最优解的性质。一般来说，这种算法容易实现、效率高，但并不保证最终的解一定是最佳的。

在实现贪心算法时，我们需要确保算法每步所做的贪心选择最终能导致全局最优解。这通常需要问题本身满足某些特殊结构，比如问题具有最优子结构或者问题具有贪心选择性质。

### 3.1.2 贪心算法与动态规划的区别

贪心算法和动态规划都是求解问题的策略，但它们的适用范围和解决问题的方式有很大区别。动态规划通常解决的是具有重叠子问题和最优子结构的问题，它保存子问题的解，避免重复计算。而贪心算法不考虑子问题，它总是做出在当前看来最好的选择，它不考虑这个选择会不会影响到子问题的解。

动态规划在每一步中会考虑所有可能的选择，然后从这些选择中挑选出一个最优解，可能需要考察多个子问题；而贪心算法则是基于当前已有的信息作出选择，不需要回溯。贪心算法相对简单高效，但适用范围有限，而动态规划适用范围更广，但计算复杂度高。

## 3.2 贪心算法的经典问题

### 3.2.1 跳