图解JavaScript算法：掌握排序与搜索的10大核心技术

# 1. JavaScript算法基础

## 1.1 JavaScript算法简介
JavaScript作为一门广泛应用于前端开发的语言，其算法能力直接影响到程序的效率和性能。算法不仅仅是为了完成任务，它还是提高代码质量、优化用户体验的利器。了解并掌握基础的算法知识，对于任何一个前端开发者来说都至关重要。

## 1.2 算法与数据结构的关系
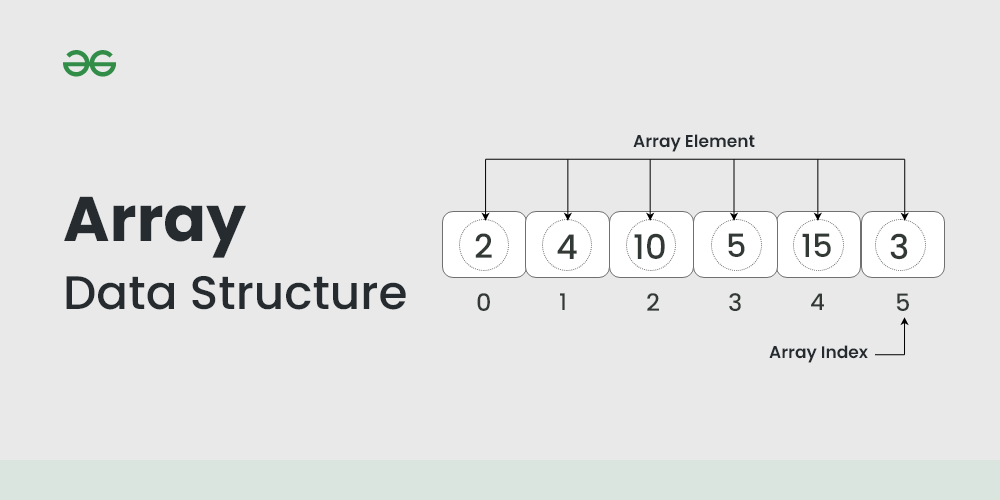
在JavaScript中，算法与数据结构是相辅相成的。数据结构决定了数据如何存储和访问，而算法则决定了解决问题的方式和效率。掌握常见的数据结构，如数组、对象、链表、栈、队列、树、图等，是理解和应用算法的基础。

## 1.3 JavaScript内置算法与操作
JavaScript为开发者提供了多种内置方法，这些方法中都包含了高效的算法实现。例如，`Array.prototype.sort`和`Array.prototype.filter`等，它们都是对特定算法的应用。了解这些内置方法背后的算法原理，可以帮助开发者更好地使用和优化它们。

在接下来的章节中，我们将深入探讨排序算法和搜索算法，揭示它们在JavaScript中的应用以及如何提高它们的性能。通过对排序和搜索算法的深入理解，我们能够编写更加高效、更加优雅的代码。

# 2. 深入理解排序算法

### 2.1 排序算法概述

排序算法是编程中最基本的算法之一，它涉及将一组数据按照特定的顺序（通常是升序或降序）重新排列。这些算法在数据处理和分析中扮演了重要角色，并且在各种不同的应用场景中都有着广泛的应用。

#### 2.1.1 排序算法的重要性与应用场景

排序算法之所以重要，是因为数据在有序状态下更容易进行检索和处理。在数据库管理系统中，排序用于高效的查找和索引；在数据可视化中，有序数据更易于绘制和理解。网络爬虫在抓取数据后，常使用排序来分类和处理信息。

#### 2.1.2 常见排序算法的时间复杂度对比

不同的排序算法根据其操作步骤的数目来评估效率，这通常以时间复杂度的形式表示。下面列出了几种常见排序算法及其时间复杂度：

- 冒泡排序: 最好情况 `O(n)`，平均情况 `O(n^2)`，最坏情况 `O(n^2)`
- 插入排序: 最好情况 `O(n)`，平均情况 `O(n^2)`，最坏情况 `O(n^2)`
- 快速排序: 最好情况 `O(n log n)`，平均情况 `O(n log n)`，最坏情况 `O(n^2)`
- 归并排序: 最好、平均、最坏情况均为 `O(n log n)`
- 堆排序: 最好、平均、最坏情况均为 `O(n log n)`

### 2.2 基本排序技术

基本排序技术包括冒泡排序、插入排序和选择排序，这些算法相对简单，易于理解和实现，但可能在效率上不如更高级的算法。

#### 2.2.1 冒泡排序与优化策略

冒泡排序是通过重复遍历要排序的数列，比较相邻元素并交换顺序错位的元素来实现排序。冒泡排序有多种优化方法，比如设置一个标志位来标记这一轮是否发生过交换，如果在一次遍历中没有发生交换，则说明数列已经有序，可以提前终止排序。

以下是冒泡排序的基本代码实现：

function bubbleSort(arr) {
    let n = arr.length;
    let swapped;
    do {
        swapped = false;
        for (let i = 1; i < n; i++) {
            if (arr[i - 1] > arr[i]) {
                // 交换元素
                let temp = arr[i - 1];
                arr[i - 1] = arr[i];
                arr[i] = temp;
                swapped = true;
            }
        }
        n--; // 减少下次遍历的范围，因为最大的已经在顶部
    } while (swapped);
    return arr;
}

#### 2.2.2 插入排序及其改进方法

插入排序通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。它的工作方式类似于我们排序扑克牌。插入排序在数组几乎有序的情况下可以表现得非常好，并且它的最坏情况时间复杂度为 `O(n^2)`。

function insertionSort(arr) {
    let len = arr.length;
    let preIndex, current;
    for (let i = 1; i < len; i++) {
        preIndex = i - 1;
        current = arr[i];
        while (preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
    return arr;
}

#### 2.2.3 选择排序原理及应用

选择排序是一种原址比较排序算法。它的工作原理是每次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

function selectionSort(arr) {
    let len = arr.length;
    let min;
    for (let i = 0; i < len - 1; i++) {
        min = i;
        for (let j = i + 1; j < len; j++) {
            if (arr[j] < arr[min]) {
                min = j;
            }
        }
        if (i != min) {
            let temp = arr[i];
            arr[i] = arr[min];
            arr[min] = temp;
        }
    }
    return arr;
}

### 2.3 高级排序算法

高级排序算法，如快速排序、归并排序和堆排序，是为了解决基本排序技术在处理大数据集时的效率问题而设计的。

#### 2.3.1 快速排序的原理与实现

快速排序是一种分而治之的排序算法。它选取一个元素作为基准值，将数组分为两部分，一部分包含小于基准值的元素，另一部分包含大于基准值的元素。该算法递归地进行下去，直到所有数据都是有序的。

function quickSort(arr) {
    if (arr.length <= 1) {
        return arr;
    }
    let pivot = arr[0];
    let left = [];
    let right = [];

    for (let i = 1; i < arr.length; i++) {
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }
    return quickSort(left).concat(pivot, quickSort(right));
}

#### 2.3.2 归并排序的过程和效率

归并排序的核心思想是将两个或两个以上的有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后把有序子序列合并为整体有序序列。

function mergeSort(arr) {
    if (arr.length <= 1) {
        return arr;
    }
    let mid = Math.floor(arr.length / 2);
    let left = arr.slice(0, mid);
    let right = arr.slice(mid);

    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
    let result = [];
    while (left.length && right.length) {
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
        }
    }
    return result.concat(left, right);
}

#### 2.3.3 堆排序的逻辑和性能分析

堆排序是利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

function heapSort(arr) {
    let n = arr.length;

    // 构建堆（重新排列数组）
    for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // 一个个从堆顶取出元素
    for (let i = n - 1; i > 0; i--) {
        // 将当前根节点放到数组的末尾
        let temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;

        // 调用 max heapify 在减小的堆上
        heapify(arr, i, 0);
    }
    return arr;
}

function heapify(arr, n, i) {
    let largest = i; // 初始化最大为根
    let left = 2 * i + 1; // 左子节点
    let right = 2 * i + 2; // 右子节点

    // 如果左子节点大于根节点
    if (left < n && arr[i] < arr[left]) {
        largest = left;
    }

    // 如果右子节点比最大的还大
    if (right < n && arr[largest] < arr[right]) {
        largest = right;
    }

    // 如果最大不是根节点
    if (largest != i) {
        let swap = arr[i];
        arr[i] = arr[largest];
        arr[largest] = swap;

        // 递归地定义子堆
        heapify(arr, n, largest);
    }
}

### 2.4 排序算法比较

下面是一个对比表，列出了一些我们已经讨论过的排序算法的特点：

| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 是否稳定 | 是否原地 |
| --- | --- | --- | --- | --- | --- |
| 冒泡排序 | O(n^2) | O(n^2) | O(1) | 是 | 是 |
| 插入排序 | O(n^2) | O(n^2) | O(1) | 是 | 是 |
| 选择排序 | O(n^2) | O(n^2) | O(1) | 否 | 是 |
| 快速排序 | O(n log n) | O(n^2) | O(log n) | 否 | 是 |
| 归并排序 | O(n log n) | O(n log n) | O(n) | 是 | 否 |
| 堆排序 | O(n log n) | O(n log n) | O(1) | 否 | 是 |

通过这些数据，我们可以看到，对于原地排序来说，快速排序通常会是一个不错的选择，因为它的平均时间复杂度是最低的。但如果稳定性是必要的，那么冒泡排序或者插入排序可能会更合适。

请在实际应用场景中仔细权衡排序算法的选择，了解其优缺点和适用性。在下文中，我们将进一步探索搜索算法的各个方面。

# 3. 探索搜索算法

## 搜索算法基础

### 线性搜索与二分搜索的对比

线性搜索是最简单直观的搜索算法，其过程是将每个元素逐一与目标值比较，适用于未排序的线性表。假设有一个数组 `arr`，线性搜索会从数组的第一个元素开始，依次检查每个元素是否等于目标值。如果数组长度为 `n`，线性搜索的平均时间复杂度是 O(n)，在最坏的情况下，时间复杂度为 O(n)。

二分搜索是一种高效的搜索算法，它适用于有序数组，并通过不断缩小查找范围来加快搜索速度。二分搜索开始时，会先比较数组中间的元素与目标值，如果相等则搜索成功。如果目标值大于中间元素，则搜索范围缩小到右半部分；如果小于中间元素，则缩小到左半部分。这个过程会持续下去，直到找到目标值或范围缩小至为空。在最佳情况下，二分搜索的时间复杂度为 O(1)，平均情况下为 O(log n)。

以下是线性搜索和二分搜索在JavaScript中的实现：

**线性搜索实现**

function linearSearch(arr, target) {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === target) {
            return i; // 找到目标，返回索引
        }
    }
    return -1; // 未找到目标，返回-1
}

**二分搜索实现**

function binarySearch(arr, target) {
    let left = 0;
    let right = arr.length - 1;

    while (left <= right) {
        const mid = Math.floor((left + right) / 2);
        if (arr[mid] === target) {
            return mid; // 找到目标，返回索引
        } else if (arr[mid] < target) {
            left = mid + 1; // 缩小搜索范围到右半部分
        } else {
            right = mid - 1; // 缩小搜索范围到左半部分
        }
    }
    return -1; // 未找到目标，返回-1
}

### 搜索算法的时间复杂度分析

在搜索算法中，时间复杂度是衡量算法性能的关键因素之一。时间复杂度通常与数据结构和数据量的大小有关。

线性搜索由于其逐个检查元素的特性，时间复杂度始终为 O(n)，这意味着算法的执行时间与数据集的大小成正比。当数据量很大时，线性搜索可能变得非常低效。

相比之下，二分搜索极大地提高了搜索效率。在有序数组中，二分搜索的时间复杂度为 O(log n)，是线性搜索时间复杂度的对数级别。因此，即使数据集的大小增加，二分搜索所需的时间也只会缓慢增加。

值得注意的是，二分搜索要求数据必须是有序的，这就引入了排序的开销。如果数据未排序，且数据量很大，那么排序所消耗的时间可能会超过二分搜索的效率提升。因此，在实际应用中，需要根据具体情况来选择适合的搜索算法。

## 二分搜索及其变种

### 传统二分搜索的工作原理

二分搜索的基本原理已经在上文中介绍过。在这里，我们将深入探讨二分搜索在实际应用中的一些变种及其优化。

首先，标准的二分搜索假设数组是已经排好序的。如果没有排序，需要先进行排序，这个额外的步骤会增加算法的总体时间复杂度。在JavaScript中，可以通过`Array.prototype.sort`方法来对数组进行排序，然后再使用二分搜索。

一个标准的二分搜索通常在找到目标值后返回其在数组中的索引，如果没有找到则返回-1。不过，二分搜索还可以返回目标值不存在的插入位置，这对于某些应用场景（如实现有序数组的插入操作）非常有用。

### 二分搜索的迭代与递归实现

在实现二分搜索时，可以采用迭代或递归两种方式。迭代版本使用循环结构，而递归版本则使用递归函数。

**迭代实现**

迭代实现较为直观，使用while循环维持搜索范围，并逐步缩小查找区间：

function binarySearchIterative(arr, target) {
    let left = 0;
    let right = arr.length - 1;
    while (left <= right) {
        const mid = Math.floor((left + right) / 2);
        if (arr[mid] === target) {
            return mid;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1; // 如果没有找到目标值，返回-1
}

**递归实现**

递归实现则将问题简化，通过递归调用自身来缩小搜索范围：

function binarySearchRecursive(arr, target, left, right) {
    if (left > right) {
        return -1; // 超出范围，未找到目标值
    }
    const mid = Math.floor((left + right) / 2);
    if (arr[mid] === target) {
        return mid;
    } else if (arr[mid] < target) {
        return binarySearchRecursive(arr, target, mid + 1, right);
    } else {
        return binarySearchRecursive(arr, target, left, mid - 1);
    }
}

在递归实现中，我们添加了额外的参数`left`和`right`来标记当前的搜索范围。通常第一次调用这个递归函数时，`left`为0，`right`为`arr.length - 1`。

### 二分搜索在实际问题中的应用

二分搜索在很多实际问题中都非常有用，尤其是在需要频繁进行查找的场景中，比如在Web开发中搜索框的自动完成功能。此外，在一些需要计算数值的领域中，二分搜索可以用于查找特定的临界点，例如求解方程的根或优化问题。

例如，在实现一个功能完备的电子商务网站时，二分搜索可以帮助提高商品查找的效率。当用户在搜索栏输入关键词，系统可以快速地在商品列表中进行二分搜索以缩小待匹配的商品范围，从而为用户提供更快的反馈。

## 高级搜索技术

### 跳表搜索算法原理

跳表（Skip List）是一种可以替代平衡树的数据结构，它通过在原始链表的基础上增加多级索引来提高查找速度。跳表中的每个节点可能包含多个指向其他节点的指针，这些指针指向不同层级的节点。最低层的节点构成原始链表，而较高层的节点则是原始链表中部分节点的子集。

查找时，算法首先从最高层的链表开始搜索，找到当前节点值小于或等于目标值的最大节点。然后，算法下降到下一层，重复这个过程，直到到达最低层。跳表的搜索时间复杂度为 O(log n)，与平衡树类似，但实现起来比平衡树简单。

### 字符串匹配算法：KMP与Boyer-Moore

字符串匹配是搜索算法中的一个重要分支，其中最著名的两个算法是KMP（Knuth-Morris-Pratt）和Boyer-Moore。

KMP算法通过构建一个部分匹配表（也称为“前缀表”），来避免在不匹配时从头开始搜索。该表记录了模式串中每个位置的最长相同前后缀长度，一旦在主串中出现不匹配情况，算法就可以根据部分匹配表跳过一些不必要的比较。

Boyer-Moore算法是一种后缀比较算法，它从模式串的末尾开始向前匹配。Boyer-Moore算法特别擅长处理包含大量重复字符的模式串，它的两个主要优化策略是坏字符规则和好后缀规则。

坏字符规则关注的是主串中与模式串不匹配的字符，根据这个字符在模式串中出现的位置，算法可以跳过一定长度的比较。

好后缀规则则是当模式串与主串的某个后缀匹配时，算法尝试将模式串滑动到与该后缀对齐的位置。通过这种规则，Boyer-Moore算法能够更快地找到匹配项。

这两种算法都旨在提高字符串匹配的效率，特别是在处理大型文本或进行文本编辑器的查找功能时表现尤为出色。

通过本章节的介绍，读者应该对搜索算法有了一个深入的了解，从基本的线性搜索和二分搜索，到更高级的跳表和字符串匹配算法，每种算法都有其独特之处和适用场景。在实际开发过程中，根据应用场景选择合适的搜索算法，不仅可以提高程序的效率，还能优化用户体验。

# 4. 图解排序与搜索算法的实践应用

排序和搜索算法是计算机科学领域中非常重要的基础算法，它们在工程实践中的应用广泛且深入。本章节将通过具体的案例和图解来展示排序与搜索算法的实际应用，帮助读者更好地理解这些算法在现实世界问题中的解决方案。

## 4.1 排序算法的工程应用

排序算法是处理数据时不可或缺的工具，它们确保数据按照特定的顺序进行排列，便于检索、分析和展示。

### 4.1.1 数组数据排序的常见场景

在各种编程应用中，数组是最常见的数据结构之一。排序数组是许多场景中的基础操作。例如，一个电子商务网站需要对商品价格进行排序，或者一个社交媒体平台需要根据用户行为对帖子进行排序显示。

// JavaScript 示例：数组排序
let prices = [5.99, 3.50, 7.45, 2.20, 8.11];
prices.sort((a, b) => a - b); // 升序排序
console.log(prices); // 输出排序后的数组

在上述JavaScript代码中，我们使用了数组自带的 `sort()` 方法对价格进行升序排序。这是排序算法应用中最简单的例子，但对于大型数据集，这种方法的效率可能不够理想。

### 4.1.2 排序算法在前端框架中的运用

在前端开发中，排序通常用于处理表格数据、搜索结果或者列表展示等。如React或Vue等现代JavaScript框架中，我们可以利用虚拟DOM来减少不必要的重绘和重排。

// React 示例：利用状态管理进行排序
***ponent {
  state = { products: [] };

  sortProducts = (field) => {
    let sortedProducts = this.state.products.slice().sort((a, b) => {
      if (a[field] < b[field]) return -1;
      if (a[field] > b[field]) return 1;
      return 0;
    });

    this.setState({ products: sortedProducts });
  };

  render() {
    return (
      <div>
        <button onClick={() => this.sortProducts('price')}>Sort by Price</button>
        <ul>
          {this.state.products.map(product => (
            <li key={product.id}>{product.name} - ${product.price}</li>
          ))}
        </ul>
      </div>
    );
  }
}

在此代码中，我们创建了一个组件来展示产品列表，并提供了一个按钮来根据价格排序。点击按钮会触发 `sortProducts` 方法，该方法将产品数组根据价格排序，并更新组件状态。

## 4.2 搜索算法在Web开发中的应用

搜索是用户与应用程序交互的常见方式之一。有效的搜索算法可以快速地从数据集中检索出用户需要的信息。

### 4.2.1 搜索功能在电子商务网站的实现

在电子商务网站中，高效的搜索功能是至关重要的。用户需要快速找到他们想要购买的商品，无论是通过关键字还是分类搜索。

// JavaScript 示例：实现简单的搜索功能
let products = [
  { id: 1, name: "Laptop", category: "Electronics" },
  { id: 2, name: "Coffee Mug", category: "Household" },
  // ...其他商品数据
];

function searchProducts(query) {
  return products.filter(product =>
    product.name.toLowerCase().includes(query.toLowerCase())
  );
}

// 使用搜索功能
let query = "Laptop";
let searchResults = searchProducts(query);

console.log(searchResults); // 输出搜索结果

在这个示例中，我们定义了一个 `searchProducts` 函数，它接受一个查询字符串作为参数，并返回一个包含匹配结果的数组。这里我们使用了JavaScript数组的 `filter` 方法和字符串的 `includes` 方法来实现搜索功能。

### 4.2.2 二分搜索在页面渲染优化中的应用

二分搜索不仅在数据查找中效率高，也可以用于优化Web页面的渲染。例如，如果页面内容是根据某种顺序排列的，我们可以使用二分搜索来确定特定内容在DOM中的位置，从而避免全页面的扫描。

// JavaScript 示例：二分搜索在页面渲染优化中的应用
function binarySearchPage(contentList, target) {
  let low = 0;
  let high = contentList.length - 1;
  let mid;

  while (low <= high) {
    mid = low + ((high - low) >> 1);
    if (contentList[mid].id === target) {
      return mid; // 找到目标，返回其在列表中的索引
    } else if (contentList[mid].id < target) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }
  return -1; // 未找到目标，返回-1
}

// 页面内容列表
let contentList = [
  { id: 1, title: "Content 1" },
  { id: 2, title: "Content 2" },
  // ...其他内容
];

// 目标内容ID
let targetId = 10;

// 执行二分搜索
let index = binarySearchPage(contentList, targetId);

if (index !== -1) {
  // 目标内容在DOM中的位置
  const targetElement = document.getElementById(`content-${targetId}`);
  // 优化渲染逻辑
}

在这个代码示例中，我们首先定义了一个 `binarySearchPage` 函数来实现二分搜索，然后通过搜索结果确定了目标内容在页面中的位置，并进行了优化处理。

通过上述实践应用的例子，我们可以看到排序和搜索算法在Web开发中的重要性。它们不仅能够帮助我们更高效地处理数据，还能够在用户体验方面起到关键作用。接下来的章节将会进一步探讨排序与搜索算法在大数据处理和用户体验提升中的作用。

# 5. JavaScript算法进阶技巧

## 5.1 算法性能优化

在JavaScript中，性能优化是确保应用程序高效运行的关键。理解时间复杂度和空间复杂度可以帮助我们编写更高效的算法。时间复杂度关注的是算法执行时间随着输入规模增加的变化趋势，而空间复杂度则关注算法在运行过程中所需的存储空间随输入规模增加的变化趋势。通过合理选择数据结构和优化算法逻辑，我们可以显著提升程序性能。

### 5.1.1 时间复杂度和空间复杂度的优化策略

时间复杂度通常用大O表示法来描述。例如，O(1)代表常数时间复杂度，O(n)代表线性时间复杂度。在实现算法时，我们应当尽量减少不必要的循环，采用分治、动态规划等策略来降低复杂度。

**示例代码：**

function linearSearch(array, target) {
  for (let i = 0; i < array.length; i++) {
    if (array[i] === target) {
      return i;
    }
  }
  return -1;
}

在上述代码中，时间复杂度为O(n)，因为我们需要遍历整个数组来查找目标值。为了优化这个搜索算法，我们可以使用二分搜索替代线性搜索，将时间复杂度降低到O(log n)。

空间复杂度是衡量算法所需额外空间的指标。例如，递归算法可能会产生大量的栈空间需求，这可能导致栈溢出错误。在编写代码时，应尽量避免不必要的空间开销，如避免创建大型的临时数组。

**示例代码：**

function factorial(n) {
  if (n === 1) return 1;
  return n * factorial(n - 1);
}

在上述递归实现的阶乘函数中，每一次函数调用都会在调用栈上增加一层，空间复杂度为O(n)。为了避免这样的情况，可以使用迭代的方法来实现阶乘，从而减少空间复杂度。

### 5.1.2 使用缓存优化算法性能

缓存是一种常用的技术，它可以存储昂贵计算的结果，以便在后续的调用中可以快速访问。在JavaScript中，我们可以使用对象或者ES6引入的`Map`数据结构来实现缓存。

**示例代码：**

const cache = new Map();

function fibonacci(n) {
  if (cache.has(n)) {
    return cache.get(n);
  }
  if (n <= 1) {
    cache.set(n, n);
    return n;
  }
  const result = fibonacci(n - 1) + fibonacci(n - 2);
  cache.set(n, result);
  return result;
}

在上述斐波那契数列函数中，我们使用了`Map`对象来缓存已经计算过的值。这样，在后续的计算中，如果遇到已经计算过的结果，就可以直接从缓存中获取，从而减少计算量和提高算法性能。

在实际开发中，我们还可以使用装饰器模式或者函数式编程中的高阶函数来实现缓存，以及利用现代JavaScript引擎的优化特性，如尾调用优化等。

## 5.2 算法思想在数据结构中的应用

数据结构是组织和存储数据的方式，而算法则定义了对这些数据进行处理的步骤。将算法思想应用于数据结构，可以大大提升数据处理的效率。下面是两种重要的数据结构——哈希表和树形结构，它们在各种应用场景中发挥着关键作用。

### 5.2.1 哈希表在快速检索中的应用

哈希表是一种支持快速插入、删除和查找操作的数据结构。它通过一个哈希函数将键映射到存储位置，从而实现快速访问。在JavaScript中，对象可以被视为一种哈希表。

**示例代码：**

function hashFunction(key, tableSize) {
  let hash = 0;
  for (let i = 0; i < key.length; i++) {
    hash = (hash + key.charCodeAt(i)) % tableSize;
  }
  return hash;
}

const hashTableSize = 100;
const hashTable = new Array(hashTableSize);

function put(key, value) {
  const index = hashFunction(key, hashTableSize);
  if (hashTable[index]) {
    hashTable[index].push({key, value});
  } else {
    hashTable[index] = [{key, value}];
  }
}

function get(key) {
  const index = hashFunction(key, hashTableSize);
  if (hashTable[index]) {
    for (let i = 0; i < hashTable[index].length; i++) {
      if (hashTable[index][i].key === key) {
        return hashTable[index][i].value;
      }
    }
  }
  return null;
}

在这个简单的哈希表实现中，我们定义了一个`hashFunction`函数，它将字符串键转换为数组索引。`put`方法将键值对插入哈希表，而`get`方法则根据键快速检索值。哈希表的平均查找时间复杂度为O(1)，但是在最差情况下，例如当所有的键都映射到同一个索引时，时间复杂度会退化为O(n)。为了防止这种情况，我们通常需要对冲突的键进行处理，例如使用链地址法或开放寻址法。

### 5.2.2 树形结构在复杂数据处理中的作用

树形结构是一种非常重要的数据结构，它特别适合用来表示具有层级关系的数据。在JavaScript中，虽然没有内置的树形数据结构，但我们可以自行实现。

**示例代码：**

class TreeNode {
  constructor(value) {
    this.value = value;
    this.children = [];
  }

  addChild(childNode) {
    this.children.push(childNode);
  }
}

class BinaryTree {
  constructor(rootValue) {
    this.root = new TreeNode(rootValue);
  }

  add(value, parentValue) {
    const parentNode = this.find(parentValue);
    const newNode = new TreeNode(value);
    if (parentNode) {
      parentNode.addChild(newNode);
    }
  }

  find(value) {
    const nodes = [this.root];
    while (nodes.length > 0) {
      const currentNode = nodes.shift();
      if (currentNode.value === value) {
        return currentNode;
      }
      nodes.push(...currentNode.children);
    }
    return null;
  }
}

// 示例使用
const tree = new BinaryTree(1);
tree.add(2, 1);
tree.add(3, 1);
tree.add(4, 2);

console.log(tree.find(2)); // 输出: TreeNode { value: 2, children: [TreeNode { value: 4, children: [] }] }

在这个简单的二叉树实现中，我们创建了`TreeNode`类来表示树的节点，并且创建了`BinaryTree`类来构建和管理树结构。`add`方法允许我们将新的节点添加到树中，而`find`方法则允许我们根据值查找节点。树形结构在复杂数据处理中的作用非常广泛，例如在数据库索引、文件系统以及各种高级搜索算法中都有应用。

在本章节中，我们已经深入探讨了如何在JavaScript中实现和优化算法。我们从性能优化的角度分析了时间复杂度和空间复杂度，并且介绍了使用缓存来提升性能的策略。此外，我们还看到了如何将算法思想应用到数据结构中，特别是哈希表和树形结构。这些知识和技能对于任何希望在编程上达到高级水平的开发者来说都是至关重要的。

在下一章中，我们将探索算法在实际问题中的应用，了解如何通过算法来解决数据去重、归类以及动态数据处理等实际问题，并探讨如何将算法与现代Web技术结合，以提升用户体验和处理大数据。

# 6. 算法实战案例分析

在前面的章节中，我们已经详细学习了排序和搜索算法的基础知识，深入探讨了它们的内部原理和各种高级技术。现在，让我们将这些理论知识应用于实际案例中，以便更全面地理解算法如何在现实世界中解决复杂问题。

## 6.1 实际问题的算法解决方案

### 6.1.1 算法在数据去重和归类中的应用

数据去重和归类是数据处理中常见的问题，特别是在大数据场景下，重复数据的处理对于资源利用和数据准确性至关重要。

一个典型的算法实现是使用哈希表来去除数组中的重复项。以下是一个基本的JavaScript实现示例：

function removeDuplicates(arr) {
    const seen = new Set();
    const unique = [];
    for (let item of arr) {
        if (!seen.has(item)) {
            unique.push(item);
            seen.add(item);
        }
    }
    return unique;
}

const arrayWithDuplicates = [1, 2, 3, 2, 1, 4, 5];
console.log(removeDuplicates(arrayWithDuplicates)); // 输出: [1, 2, 3, 4, 5]

### 6.1.2 算法在动态数据处理中的实战演练

在实时系统中，数据是持续变化的。使用合适的数据结构和算法可以有效地处理这些动态数据。例如，可以使用二叉搜索树来存储和处理实时数据。

考虑一个实时数据流处理的场景，比如股票价格的实时更新。我们可以利用红黑树（一种自平衡的二叉搜索树）来快速插入和查询当前的最低价或最高价。

class RedBlackTree {
    // 省略红黑树的实现细节
}

// 实时接收新的股票价格并更新树结构
function updateStockPrice(stockSymbol, newPrice) {
    const stockTree = getStockTree(stockSymbol); // 获取特定股票的红黑树
    stockTree.insert(newPrice); // 插入新价格
    console.log(`The current highest price for ${stockSymbol} is ${stockTree.max()}`);
}

// 假设我们有一函数来获取特定股票的树
function getStockTree(stockSymbol) {
    // 省略树的获取逻辑
}

// 实时数据更新
***StockPrice('AAPL', 150.25);
updateStockPrice('GOOGL', 2800.50);

## 6.2 算法与现代Web技术的结合

### 6.2.1 算法在大数据处理中的重要性

在Web开发中，尤其是涉及到大数据处理的场景，算法的效率直接关系到系统性能。利用高效的排序和搜索算法可以大大减少数据处理时间，提高用户响应速度。

例如，电商平台在处理用户搜索请求时，通常需要对上亿的商品信息进行筛选。使用合适的算法进行数据预处理，比如通过索引技术提高查询效率，可以显著提升用户在浏览商品时的体验。

### 6.2.2 利用算法提升用户体验的案例研究

算法不仅可以提高系统性能，还可以用来改善用户体验。例如，搜索引擎通过优化排序算法，可以为用户返回更相关的结果。

// 搜索函数示例
function searchItems(query, items) {
    // 对items进行排序算法，例如快速排序
    const sortedItems = quickSort(items, (a, b) => a.score - b.score);
    return sortedItems.filter(item => item.name.includes(query));
}

const searchQuery = 'smartphone';
const items = [
    { name: 'Smartphone A', score: 90 },
    { name: 'Smartphone B', score: 95 },
    // ... 其他商品
];

const searchResults = searchItems(searchQuery, items);
console.log(searchResults); // 输出过滤和排序后的商品列表

通过上述案例，我们可以看到算法是如何在实际问题解决中发挥作用的。在接下来的章节中，我们将继续深入探讨算法的应用，并提供更多实战案例来加深理解。