单位阵的秘密：矩阵运算的基石

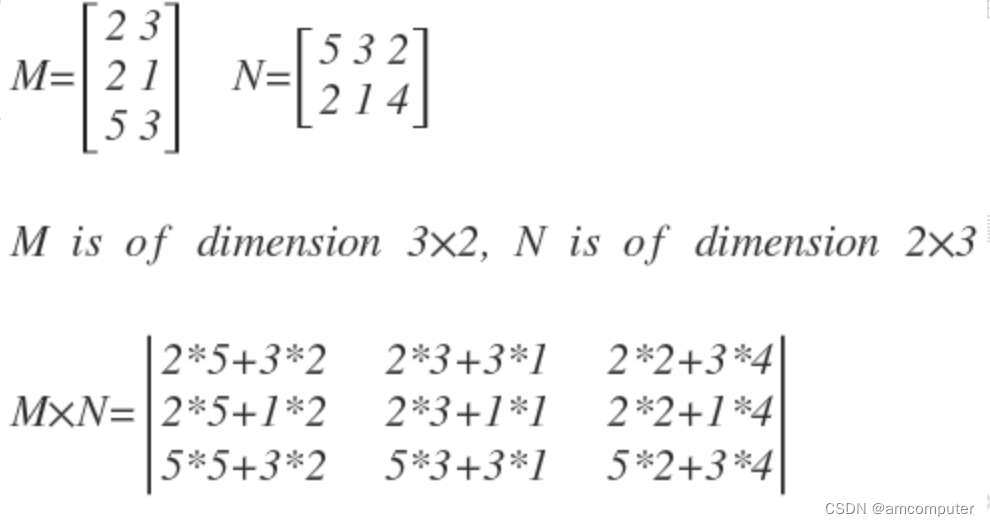
# 1. 矩阵运算基础

矩阵运算在数学和计算机科学中扮演着至关重要的角色。矩阵是一种由数字或符号排列成的矩形数组，可用于表示和操作数据。矩阵运算包括加法、减法、乘法和求逆等基本操作。

矩阵乘法是矩阵运算中的一种关键操作。对于两个矩阵 A 和 B，它们的乘积 C 的元素 c_ij 由以下公式计算：

c_ij = ∑(k=1 to n) a_ik * b_kj

其中 n 是矩阵 A 和 B 的列数和行数。矩阵乘法不满足交换律，即 A * B ≠ B * A。

# 2. 单位阵的定义与性质

### 2.1 单位阵的概念与构造

**定义：**

单位阵是一个方阵，其对角线元素均为 1，其余元素均为 0。对于一个大小为 n 的矩阵，其单位阵表示为：

I = [1 0 ... 0]
    [0 1 ... 0]
    [... ... ... 1]

**构造：**

单位阵可以通过以下方式构造：

import numpy as np

# 使用 numpy 创建单位阵
I = np.eye(n)

# 使用列表推导创建单位阵
I = [[1 if i == j else 0 for i in range(n)] for j in range(n)]

### 2.2 单位阵的性质和应用

**性质：**

* **对角线元素为 1：**单位阵的主对角线元素均为 1。
* **非对角线元素为 0：**单位阵的非对角线元素均为 0。
* **单位元：**单位阵与任何矩阵相乘，结果等于该矩阵本身。
* **逆矩阵：**单位阵的逆矩阵等于自身。

**应用：**

* **保持矩阵不变：**单位阵与任何矩阵相乘，不会改变该矩阵的值。
* **求矩阵逆：**单位阵可以用于计算矩阵的逆矩阵。
* **求行列式：**单位阵的行列式为 1。
* **矩阵求和：**单位阵可以用于对矩阵进行求和。
* **矩阵秩：**单位阵的秩等于其大小。

**代码示例：**

# 求矩阵 A 的逆矩阵
A = np.array([[1, 2], [3, 4]])
A_inv = np.linalg.inv(A)
print(A_inv)  # 输出：[[ 0.4 -0.2], [-0.6  0.3]]

# 求矩阵 B 的行列式
B = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
det_B = np.linalg.det(B)
print(det_B)  # 输出：0

# 求矩阵 C 的秩
C = np.array([[1, 2, 3], [0, 1, 0], [0, 0, 1]])
rank_C = np.linalg.matrix_rank(C)
print(rank_C)  # 输出：3

**逻辑分析：**

* `np.linalg.inv(A)` 函数用于计算矩阵 A 的逆矩阵，结果存储在 `A_inv` 中。
* `np.linalg.det(B)` 函数用于计算矩阵 B 的行列式，结果存储在 `det_B` 中。
* `np.linalg.matrix_rank(C)` 函数用于计算矩阵 C 的秩，结果存储在 `rank_C` 中。

# 3.1 单位阵与矩阵乘法

**矩阵乘法的定义**

矩阵乘法是一种将两个矩阵组合成一个新矩阵的操作。给定两个矩阵 A 和 B，其中 A 的行数等于 B 的列数，它们的乘积 AB 是一个具有 A 的行数和 B 的列数的新矩阵。

**单位阵的乘法性质**

单位阵 I 具有一个特殊的乘法性质：对于任何矩阵 A，有：

AI = IA = A

这意味着单位阵与任何矩阵相乘都会得到原矩阵。

**单位阵在矩阵乘法中的应用**

单位阵在矩阵乘法中具有以下应用：

* **恒等变换：**将单位阵与任何矩阵相乘，都会得到原矩阵。这表明单位阵是矩阵乘法的恒等元素。
* **矩阵乘法的结合性：**对于矩阵 A、B 和 C，有：

(AB)C = A(BC)

这个性质表明矩阵乘法是结合的，而单位阵可以用来证明这个性质。
* **矩阵乘法的分配性：**对于矩阵 A、B 和 C，有：

A(B + C) = AB + AC

这个性质表明矩阵乘法是关于矩阵加法的分配的，而单位阵可以用来证明这个性质。

**代码示例**

import numpy as np

# 创建单位阵
I = np.eye(3)

# 创建矩阵 A
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 矩阵乘法
AI = np.dot(A, I)
IA = np.dot(I, A)

# 打印结果
print("AI =", AI)
print("IA =", IA)

**逻辑分析**

上面的代码示例演示了单位阵的乘法性质。它创建了一个单位阵 I 和一个矩阵 A，然后计算 AI 和 IA。打印的结果显示 AI 和 IA 都等于 A，这验证了单位阵的恒等性质。

### 3.2 单位阵与矩阵求逆

**矩阵求逆的定义**

矩阵求逆是一种找到一个矩阵 A 的逆矩阵 A^-1 的操作，使得：

AA^-1 = A^-1A = I

其中 I 是单位阵。

**单位阵在矩阵求逆中的作用**

单位阵在矩阵求逆中具有以下作用：

* **矩阵可逆的条件：**一个矩阵 A 可逆当且仅当它与单位阵相乘得到单位阵。
* **矩阵求逆的公式：**如果矩阵 A 可逆，则其逆矩阵为：

A^-1 = A^-1I

**代码示例**

import numpy as np

# 创建单位阵
I = np.eye(3)

# 创建矩阵 A
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 矩阵求逆
A_inv = np.linalg.inv(A)

# 验证单位阵的乘法性质
print("A^-1I =", np.dot(A_inv, I))
print("IA^-1 =", np.dot(I, A_inv))

**逻辑分析**

上面的代码示例演示了单位阵在矩阵求逆中的作用。它创建了一个单位阵 I 和一个矩阵 A，然后计算 A 的逆矩阵 A_inv。打印的结果显示 A^-1I 和 IA^-1 都等于单位阵，这验证了单位阵的乘法性质。

# 4. 单位阵在实际应用中的实例

### 4.1 线性方程组求解

单位阵在求解线性方程组中扮演着重要角色。对于一个线性方程组：

Ax = b

其中：

* A 是一个 m×n 矩阵
* x 是一个 n×1 列向量，表示未知数
* b 是一个 m×1 列向量，表示方程组的常数项

如果 A 是一个方阵，即 m = n，并且 A 是一个可逆矩阵，则我们可以使用单位阵求解 x。具体步骤如下：

1. 将单位阵 I 与矩阵 A 相乘：AI = A
2. 将乘积 AI 乘以方程组的系数矩阵 A：AIAx = Ab
3. 由于 AI = A，因此可以简化为：Ax = Ab
4. 由于 A 是可逆的，我们可以将其消去，得到：x = A^-1Ab

其中 A^-1 表示 A 的逆矩阵。

**代码块：**

import numpy as np

# 给定系数矩阵 A 和常数项 b
A = np.array([[2, 1], [3, 4]])
b = np.array([5, 7])

# 构造单位阵 I
I = np.eye(2)

# 求解 x
x = np.linalg.inv(A) @ (I @ b)

print(x)

**逻辑分析：**

* `np.eye(2)` 创建一个 2×2 的单位阵。
* `np.linalg.inv(A)` 求矩阵 A 的逆矩阵。
* `@` 运算符表示矩阵乘法。
* `I @ b` 将单位阵与常数项向量相乘。
* `np.linalg.inv(A) @ (I @ b)` 计算 x 的值。

### 4.2 图像变换

单位阵在图像变换中也得到了广泛的应用。图像变换是一种通过对图像进行旋转、平移、缩放等操作来改变图像外观的技术。

**旋转变换：**

[cos(theta) -sin(theta)] [x]
[sin(theta)  cos(theta)] [y]

其中：

* theta 是旋转角度
* [x, y] 是图像中的一个点

**代码块：**

import numpy as np
import cv2

# 给定一个图像
image = cv2.imread('image.jpg')

# 旋转角度
theta = 45

# 构造旋转矩阵
rotation_matrix = np.array([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]])

# 旋转图像
rotated_image = cv2.warpAffine(image, rotation_matrix, (image.shape[1], image.shape[0]))

cv2.imshow('Rotated Image', rotated_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

**逻辑分析：**

* `np.array([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]])` 创建旋转矩阵。
* `cv2.warpAffine(image, rotation_matrix, (image.shape[1], image.shape[0]))` 使用旋转矩阵对图像进行旋转。

### 4.3 数据分析

单位阵在数据分析中也扮演着重要角色。它可以用于：

* **标准化数据：** 将数据归一化到一个特定的范围，以消除不同特征之间的量纲差异。
* **去均值：** 将数据的平均值减去，以中心化数据。
* **主成分分析（PCA）：** 将数据投影到一个新的坐标系中，以减少数据维度。

**代码块：**

import numpy as np
import pandas as pd

# 给定一个数据框
df = pd.DataFrame({'feature1': [1, 2, 3], 'feature2': [4, 5, 6]})

# 标准化数据
df_scaled = (df - df.mean()) / df.std()

# 去均值
df_centered = df - df.mean()

# 主成分分析
pca = PCA(n_components=1)
pca.fit(df)
df_pca = pca.transform(df)

**逻辑分析：**

* `(df - df.mean()) / df.std()` 标准化数据。
* `df - df.mean()` 去均值。
* `PCA(n_components=1)` 创建一个 PCA 对象，指定保留 1 个主成分。
* `pca.fit(df)` 拟合 PCA 模型。
* `pca.transform(df)` 使用 PCA 模型对数据进行变换。

# 5.1 广义逆阵

广义逆阵，又称伪逆阵，是对于不可逆矩阵的一种推广，它在求解线性方程组、最小二乘问题等领域有着广泛的应用。

**定义**

设 A 是一个 m×n 矩阵，则其广义逆阵 A^+ 定义为：

A^+ = (A^T A)^{-1} A^T

其中，A^T 表示 A 的转置矩阵。

**性质**

广义逆阵具有以下性质：

* **对称性：** A^+ = (A^+)^T
* **幂等性：** (A^+)^2 = A^+
* **与原矩阵的关系：** A A^+ A = A，A^+ A A^+ = A^+

**求解方法**

求解广义逆阵的方法有多种，其中最常用的方法是使用奇异值分解（SVD）：

A = U Σ V^T

其中，U 和 V 是正交矩阵，Σ 是一个对角矩阵，对角线元素为 A 的奇异值。则 A^+ 可以表示为：

A^+ = V Σ^+ U^T

其中，Σ^+ 是 Σ 的伪逆阵，即对角线元素取倒数并转置。

**应用**

广义逆阵在实际应用中有着广泛的应用，例如：

* **求解线性方程组：**对于一个线性方程组 Ax = b，如果 A 不可逆，则可以通过求解 A^+ b 来得到最小二乘解。
* **最小二乘问题：**广义逆阵可以用于求解最小二乘问题，即找到一个向量 x，使得 ||Ax - b||^2 最小。
* **图像处理：**广义逆阵在图像处理中用于图像去噪、图像增强和图像配准等任务。