【统计模型解读】：如何向团队清晰解释logit_probit回归结果？


# 摘要
统计模型在数据分析中扮演着至关重要的角色，尤其是logit与probit模型，它们广泛应用于处理分类变量。本文首先介绍了统计模型的理论基础，然后深入解释了logit和probit模型的工作原理及其在不同场景下的应用。通过实例分析，本文探讨了在实际操作中如何选择合适的模型，并解读模型结果。本文还探讨了如何有效地向团队传达logit_probit模型的相关知识，并讨论了模型结果在商业和学术领域的应用。通过模型结果的可视化展示技巧，本文旨在提高模型解读能力，并强化模型结果的沟通效率。

# 关键字
统计模型；logit模型；probit模型；分类变量；模型解读；可视化展示

参考资源链接：[R语言实现：广义线性回归——01变量的logit/probit回归分析](https://wenku.csdn.net/doc/6401abbdcce7214c316e9557?spm=1055.2635.3001.10343)
# 1. 统计模型的理论基础

在现代数据分析领域，统计模型是理解和预测复杂系统行为的关键工具。统计模型通过数学语言描述变量间的关系，以及变量与结果之间的概率联系。理解统计模型的理论基础不仅对于初学者，对于经验丰富的IT专业人员也至关重要，因为它奠定了进一步探索高级统计技术，例如logit和probit模型的基石。

## 1.1 概述统计模型的定义和目的

统计模型是对现实世界现象的数学抽象，目的是通过有限的数据来识别隐藏的模式、结构或关系。这些模型在预测、分类、决策等方面有广泛应用。模型通常包含参数，这些参数通过数据拟合过程来估计。理解模型的构建和评估过程是研究和应用统计模型的基础。

## 1.2 模型的基本组成

统计模型主要由以下几个部分组成：
- **解释变量（自变量）**：影响或解释响应变量的变量。
- **响应变量（因变量）**：模型试图解释或预测的变量。
- **参数**：模型中的常数，描述解释变量对响应变量的影响程度。
- **误差项**：表示模型中无法解释的随机变异。

通过这章的学习，我们将掌握如何建立统计模型，并了解它们如何帮助我们从数据中提取有用的信息。接下来的章节将详细探讨logit和probit模型，这两种在处理分类数据时非常有用的统计工具。

# 2. logit与probit模型详解

### 2.1 概率模型与分类变量

#### 2.1.1 概率模型的基本概念
概率模型是统计模型的一部分，它允许我们对随机事件发生的概率进行建模和预测。在概率模型中，我们经常使用概率函数来描述这些随机事件。当我们讨论分类变量时，我们通常是在探讨离散结果的概率模型，例如，某个人是否会购买某项产品，或者某项疾病是否会发展到严重阶段。

在概率模型中，我们要解决的关键问题是确定相关变量与事件发生的概率之间的关系。以逻辑回归（Logit模型）为例，它常用于处理二分类问题，即结果只有两个可能的情况。我们通过估计模型参数来确定自变量和因变量之间关系的强度和方向。

#### 2.1.2 分类变量在统计模型中的应用
分类变量是数据集中非常重要的组成部分，它广泛应用于各类统计模型中，尤其是在预测二元结果（是/否）或多项选择结果（如A、B、C）时。例如，在市场研究中，我们可能希望预测消费者是否会对某个新产品感兴趣，或者在医疗研究中，我们可能想要判断某种治疗是否对患者有效。

分类变量在统计模型中的应用需要对其编码方式进行特别处理。例如，我们可以使用虚拟变量（dummy variables）来代表那些分类特征。在这个过程中，我们为每个分类结果赋予一个二进制值（通常是0或1），以便可以将其有效地整合到回归模型中。这使得我们可以对分类变量的每个类别对目标事件的影响进行建模。

### 2.2 logit模型的工作原理

#### 2.2.1 logit模型的数学表达
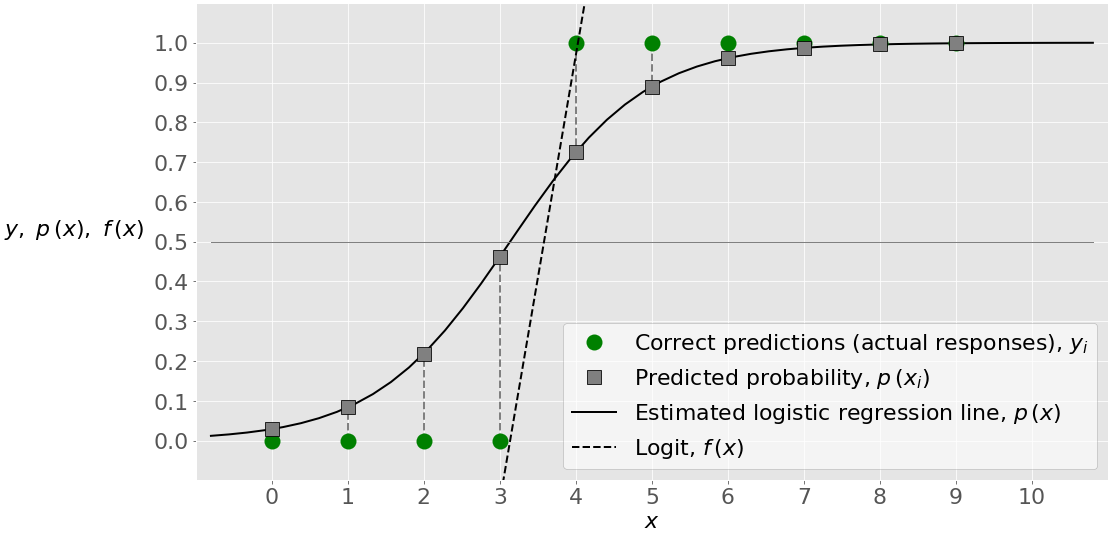
Logit模型是处理分类结果的一种回归分析方法，它特别适用于因变量是二元的情况。其核心思想是通过逻辑函数来映射线性组合的预测值到（0,1）区间，表示事件发生的概率。数学上，Logit模型可以表示为：

\[ \text{logit}(p) = \ln\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_k X_k \]

这里，\( p \) 表示事件发生的概率，\( \text{logit}(p) \) 是事件发生概率的对数几率，\( \beta_i \) 是模型参数，\( X_i \) 是解释变量。

#### 2.2.2 logit模型的参数解释和预测
在logit模型中，模型参数解释了自变量对事件发生几率的影响。具体来说，每一个参数都代表了在其他变量保持不变的情况下，自变量每改变一个单位，目标事件发生的几率变化的倍数。

例如，考虑一个logit模型，其中我们预测消费者是否会购买某一新产品：

\[ \text{logit}(p) = \beta_0 + \beta_1 \cdot \text{Age} + \beta_2 \cdot \text{Income} \]

如果 \( \beta_1 \) 的估计值为 -0.05，这表示消费者的年龄每增加一岁，购买该新产品的几率降低5%。如果 \( \beta_2 \) 的估计值为 0.02，那么消费者的收入每增加一个单位，购买该新产品的几率增加2%。

预测方面，我们首先通过模型得到logit值，然后通过逆逻辑函数将其转换为概率值。概率值可以用来预测个体属于某个类别的可能性。

### 2.3 probit模型的理论框架

#### 2.3.1 probit模型与正态分布的关系
Probit模型是另一种处理二元分类结果的模型，它与Logit模型类似，但其背后的概率分布是标准正态分布而不是逻辑分布。在Probit模型中，因变量的预测值被限制在（0,1）区间，代表事件发生的概率。

其数学表达可以写作：

\[ \text{probit}(p) = \Phi^{-1}(p) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_k X_k \]

其中 \( \Phi^{-1} \) 是标准正态累积分布函数的逆函数，\( p \) 是事件发生的概率，\( \beta_i \) 是模型参数，\( X_i \) 是解释变量。

#### 2.3.2 probit模型的参数估计与解读
Probit模型的参数估计是通过最大化似然函数来得到的，这与Logit模型类似。估计完成后，我们可以解释参数与标准正态分布中的对应概率变化之间的关系。

例如，如果我们有一个模型来预测某项治疗是否成功：

\[ \text{probit}(p) = \beta_0 + \beta_1 \cdot \text{Dosage} \]

这里，如果 \( \beta_1 \) 的估计值为 0.6，我们可以认为随着剂量的增加，治疗成功的几率增加，具体来说，剂量每增加一个单位，治疗成功的几率会增加其标准正态分布中的0.6个标准差。

请注意，Probit模