Strassen算法和Winograd算法：矩阵相乘的优化算法详解

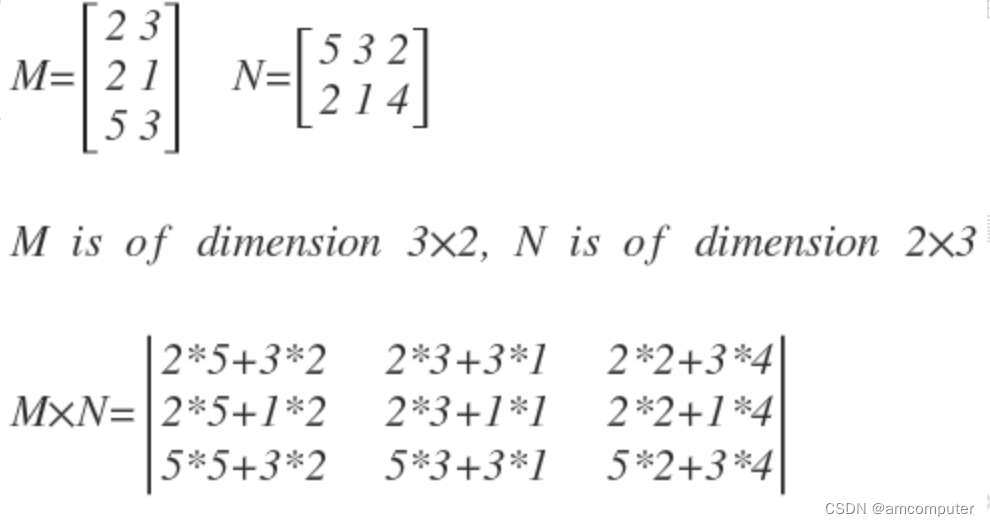
# 1. 矩阵相乘的基础**

矩阵相乘是线性代数中一项基本操作，广泛应用于计算机图形学、机器学习等领域。矩阵相乘的计算复杂度为 O(n^3)，其中 n 为矩阵的维度。

矩阵相乘的定义如下：给定两个矩阵 A 和 B，其中 A 为 m×n 矩阵，B 为 n×p 矩阵，则它们的乘积 C 为 m×p 矩阵，其元素 c_ij 由下式计算：

c_ij = ∑(a_ik * b_kj)

其中，a_ik 和 b_kj 分别为 A 和 B 中的元素。

# 2. Strassen算法

### 2.1 Strassen算法的原理

#### 2.1.1 分治策略

Strassen算法是一种分治算法，它将矩阵相乘问题分解成更小的子问题。具体来说，它将两个n×n矩阵A和B分解成四个n/2×n/2的子矩阵：

A = [A11 A12]
    [A21 A22]
B = [B11 B12]
    [B21 B22]

然后，它计算以下七个子矩阵的乘积：

C11 = A11 * B11 + A12 * B21
C12 = A11 * B12 + A12 * B22
C21 = A21 * B11 + A22 * B21
C22 = A21 * B12 + A22 * B22

最后，它将这些子矩阵组合起来得到最终的乘积矩阵C：

C = [C11 C12]
    [C21 C22]

#### 2.1.2 递归实现

Strassen算法可以递归地实现。对于两个n×n矩阵A和B，算法如下：

def strassen(A, B):
    n = A.shape[0]
    if n == 1:
        return A * B
    else:
        A11, A12, A21, A22 = A[:n//2, :n//2], A[:n//2, n//2:], A[n//2:, :n//2], A[n//2:, n//2:]
        B11, B12, B21, B22 = B[:n//2, :n//2], B[:n//2, n//2:], B[n//2:, :n//2], B[n//2:, n//2:]
        C11 = strassen(A11, B11) + strassen(A12, B21)
        C12 = strassen(A11, B12) + strassen(A12, B22)
        C21 = strassen(A21, B11) + strassen(A22, B21)
        C22 = strassen(A21, B12) + strassen(A22, B22)
        return np.concatenate((np.concatenate((C11, C12), axis=1), np.concatenate((C21, C22), axis=1)), axis=0)

### 2.2 Strassen算法的优化

#### 2.2.1 缓存优化

Strassen算法的一个优化方法是使用缓存来存储子矩阵的乘积。这可以减少重复计算的次数，从而提高算法的效率。

#### 2.2.2 并行优化

Strassen算法也可以通过并行化来优化。由于算法可以递归地实现，因此可以将不同的子矩阵乘积分配给不同的处理器并行计算。

# 3.1 Winograd算法的原理

Winograd算法是一种基于傅里叶变换和多项式乘法的矩阵相乘算法。它通过将矩阵相乘问题转化为多项式乘法问题来实现高效计算。

**3.1.1 傅里叶变换**

傅里叶变换是一种将时域信号转换为频域信号的数学变换。在Winograd算法中，傅里叶变换用于将输入矩阵转换为频域表示。频域表示中，矩阵元素的分布更加均匀，便于后续的多项式乘法操作。

**3.1.2 多项式乘法**

多项式乘法是一种计算两个多项式乘积的算法。在Winograd算法中，多项式乘法用于计算频域中矩阵元素的乘积。通过利用多项式乘法的快速算法，可以高效地完成矩阵元素的乘法运算。

**代码块：**

def winograd_multiply(A, B):
    """
    使用Winograd算法计算矩阵A和B的乘积。

    参数：
        A: 输入矩阵A。
        B: 输入矩阵B。

    返回：
        C: 矩阵A和B的乘积。